综合客运交通系统演化建模与求解

宋成举，张亚平

(1. 黑龙江工程学院 汽车与交通工程学院，黑龙江 哈尔滨 150050； 2. 哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150090)

0 引 言

综合客运交通系统是由互相补充、彼此协作、紧密配合的所有交通运输方式以及与交通运输方式相关的线路、换乘枢纽等相关资源所组成的，各种方式的连接线一般为各种方式的交通线路，而连接点则主要是换乘枢纽，这种组合可以实现各种客运方式间的有效换乘和多式联运，是一个相对完善的综合客运交通系统[1]。多种交通方式之间的竞争与合作共同促进运输资源一体化不断向前发展。因此，开展综合客运交通系统演化研究对于科学认识综合客运交通系统内部运行机制，全面把握综合客运交通系统发展方向具有重要的指导意义[2]。

综合客运交通系统是在综合交通基础上提出的，相关研究也仅有三四十年，但取得了很多代表性的研究成果。F. ÜLENGIN等[3]分析了土耳其运输网络存在的问题，提出了一个决策支持系统，以弥补缺乏交通总体规划的不足，促进分析特定政策可能对改变客运和货运交通运输方式的影响；J. C. PÉREZ等[4]应用多标准决策(MCDM)技术研究城市客运系统设计和运营等方面的最优目标，并相应的给出了实施建议；H. HAGHSHENAS等[5]构建综合客运交通系统发展政策的系统动力学模型，从环境，经济和社会可持续发展3个方面分别给出了关键指标，并建立融合关键指标的综合性指标分析系统发展趋势；李婷婷等[6]基于层级选址模型，提出了考虑能力限制的区域综合客运交通枢纽分层布局优化模型，设计免疫克隆算法并求解，最后通过算例验证了模型和算法的有效性；甘志良[7]采用综合量化分析法，构建综合客运枢纽服务水平评价指标体系，提出各指标的量化方法；傅成红[8]构建了综合交通运输系统承载力、协调性的结构模型，并建立了相应的评价体系。既有研究成果针对综合客运交通系统从建模分析等方面开展了研究，而缺乏对系统内动力建模与解析求解的相关探索。基于此，笔者在构建综合客运交通系统演化模型的基础上，应用数学方法求解模型，以剖析综合客运交通系统演化方式，明确系统内各种交通方式之间的作用机制。

1 综合客运交通系统自组织演化建模

1.1 状态变量选择

综合客运交通系统中包括公路、铁路、民航和水运4种运输方式，参照国家统计局公布的数据，以客运周转量作为描述综合客运交通系统的状态变量，它可以表征运输方式的全部劳动成果。此外，综合客运交通系统还受到系统内外诸多因素的制约，将内部因素统一记做因素集{cj}，外部因素记做f(t)，假定Xi(i=1,2,3,4)为第i种运输方式的客运周转量，则综合客运交通系统可以表示为

S=F({Xi},{cj},f(t),t)

(1)

式中：S为系统状态；F为向量函数；t为时间。

1.2 综合客运交通系统演化建模

在综合客运交通系统内外诸多因素的共同作用下，系统不断向前演化，每个时段的系统状态都取决于当前状态和系统变化，类似于流体运动，即每个流位状态都受到当前流入或流出的物质、能量和信息等因素的变化影响。从而使得综合客运交通系统的演化过程表征为一系列非线性微分方程组。

(2)

式中：x为流位向量；p为一组参数；F为非线性的向量函数。

由于综合客运交通系统满足自组织演化条件[9]，可以采用流体运动方程描述，考虑到综合客运交通系统中各子系统的发展潜力和随机因素的干扰，建立客运综合交通系统动力学演化模型。

(3)

式中：X=(X1,X2,X3,X4)分别为公路、铁路、民航和水运子系统客运周转量；M=(M1,M2,M3,M4)分别为4种运输方式的发展潜力向量；f(t)为系统所受到的随机因素变量。

1.3 模型构建

综合客运交通系统演化过程类似于人口增长过程，当各子系统发展规模相对较少时，其增长是迅速的，而当子系统规模相对多时，其增长率便会趋缓，而越靠近容量的上限时，增长率越低。因此，文中采用Logistic模型描述综合客运交通系统演化过程。

结合综合客运交通系统中系统的流体运动方程和Logistic模型，可得各子系统的自组织演化模型[9]：

(4)

式中：Ci为在当地资源和环境条件等影响下，运输方式i所能实现的最大周转量。

而在综合客运交通系统中，各种运输方式在环境资源限制的条件下自我发展的同时，它们之间还存在着非线性的竞争和协作关系，这些因素都对运输方式的发展构成了不同程度的影响。

因此，某种运输方式的发展除了包括环境限制下的自身发展，还包括运输方式之间的竞争关系对自身的影响，以及运输方式之间的协作关系对自身的影响。则式(4)可变化得：

(5)

式中：αij为运输方式j对运输方式i周转量的影响系数，αij≥0为运输方式i对运输方式j周转量起促进作用，反之则起抑制作用。

将式(5)整理后可得：

(6)

2 模型求解

上述方程为典型的非线性微分方程组，而且包含一定的随机因素。根据模型结构可以看出，该模型由两部分组成，且对于未来系统发展的影响作用存在一定的本质差别。基于此，将该方程组划分为Logistic方程部分和随机部分，分别对两部分进行求解。

2.1 Logistic方程部分求解

由于随机因素体现了系统所受到的扰动情况，在统计学上，扰动的期望值为0，为了简化方程，假定fi(t)=0。将式(6)变为

(7)

(8)

(9)

则式(9)可整理为

(10)

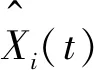
(11)

假定：

则系统误差Ei可表示为

Ei=Yi-Biλi

(12)

根据最小二乘法估计系统参数λi，可得：

(13)

2.2 随机部分求解

在Logistic方程部分求解时，假定fi(t)=0，在实际中，由于偶发效应的存在，使得系统随机涨落的难以忽略。因此，为了体现系统偶然的演化趋势，则必须考虑综合客运交通系统演化过程中所受到随机因素的影响。

在前文中已经求出系数λi，将其带入式(12)，可以求得系统误差项E=[E1,E2,E3]，利用K阶Fourier级数拟合，可得拟合方程Fi(t)。

(14)

此外，根据定义可得：

(15)

同时求导可得：

(16)

整理得：

(17)

则公式(5)中的随机项可求，综合客运交通系统演化模型可以通过上述方法求得。

3 算例分析

3.1 数据拟合

查询哈尔滨统计信息网所公布的哈尔滨统计月报(2011年—2013年)，收集关于哈尔滨市旅客周转量2011年—2013年的月度统计数据，由于哈尔滨的水运以货运为主，故在统计中未将水运方式计入。其数据汇总至表1。

表1 哈尔滨市客运周转量汇总Table 1 The passenger turnover summary for Harbin 百万人公里

代入式(11)中，取Δt=1，则

将计算结果代入式(10)，整理得误差序列E=[E1,E2,E3]。

利用Fourier级数逼近拟合，Fourier级数的公式可以表示为

(18)

式中：n为阶数；ω为拟合角速度；ai，bi为待标定参数。

根据误差序列E=[E1,E2,E3]，利用6级Fourier级数，取置信概率为95%，拟合曲线如图1：

图1 误差项Fourier级数拟合Fig. 1 The Fourier series fitting for error

拟合方程的参数值见表2。

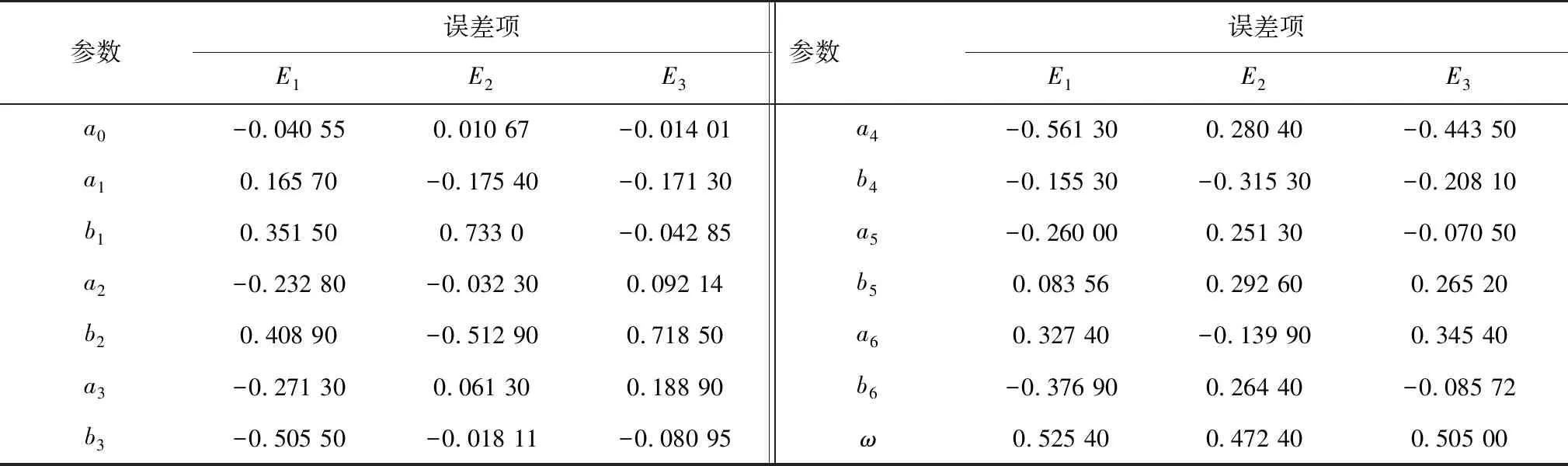
表2 误差项Fourier级数拟合参数值Table 2 The parameter value of the Fourier series fitting for error

(19)

则式(6)可以表示为

(20)

利用MATLAB中simulink绘制方程曲线，得扰动条件下3种客运方式的周转量变化曲线，如图2。

图2 哈尔滨市综合客运交通系统拟合Fig. 2 Fitting chart of the integrated passenger transport system in Harbin

从图2中可以看出，拟合值基本能够反映出统计值的波动情况，不但可以反映出综合客运交通系统的固定增长，而且能够较好的反映系统中存在的随机因素，可以进一步推广并用以系统发展预测研究。

3.2 精度检验

根据前文建立的拟合方程，对哈尔滨综合客运交通系统演化趋势进行预测，可得2013年11月份的客运结构预测和实际值的对比情况，见表3。

表3 宏观结构数据对比Table 3 Comparison of macro structural 百万人公里

从表3中可以看出，综合客运交通系统演化模型的预测精度都在10%以内，预测结果稳定可靠，能够满足研究需要。

通过对哈尔滨市综合客运交通系统的实证分析，表明采用Logistic方程与Fourier级数联合可以描述综合客运交通系统的演化进程。同时也说明了综合客运交通系统演化的动力来源于系统内部和外部因素的共同作用。

4 结 论

以综合客运交通系统为研究对象，以客运周转量为系统变量，建立综合客运交通系统演化模型，并对模型求解和实例验证。研究得到结论如下：

1)Logistics非线性方程组可以描述综合客运交通系统演化过程。

2)综合客运交通系统演化方程能够拆分成Logistic方程部分和随机部分，其中Logistic方程部分采用矩阵最小二乘法拟合，随机部分采用K阶Fourier级数拟合。

3)以哈尔滨市综合客运交通系统为例，标定模型参数，计算结果表明该方法预测综合客运交通系统精度可以满足需求。