基于ARIMA和ARCH模型的上海出口集装箱运价指数短期分析与预测

李志斌 王瀛帜 李柯男 涂贵辉

摘  要：上海出口集装箱运价指数（SCFI）是反映市场运价指数行情变化趋势的主要指标。本文首先运用ADF检验对SCFI序列进行检验，得出SCFI序列是一个单位根过程，是非平稳的;然后，对SCFI 序列进行一阶差分，差分后是平稳的，通过构建ARIMA模型，得出SCFI的ARIMA（2，1，2）模型。针对SCFI指数的波动性，研究其对数序列ln（SCFI），通过ADF检验判断ln（SCFI）序列也是一阶单整的。最后，运用ARCH LM检验得出SCFI对数序列存在ARCH效应，并用ARCH （1，1） 模型消除残差序列的条件异方差性。利用Eviews软件和Crystal ball进行实践操作，对研究问题进行求解，旨在了解上海出口集装箱运输市场形式，判断市场走向，为相关港航企业经营决策以及政府部门调控管理提供参考。

关键词：上海出口集装箱运价指数;ADF检验;ARIMA模型;ARCH模型

1 绪 论

1.1 研究背景

上海是国际知名的贸易物流中心，位于东南沿海，地理位置优越，邻近国际航运主干道，适宜建设港口，依托长三角作为经济腹地，每年都有大量的集装箱货物完成进出口贸易。上海港理所当然地承担起集装箱进出口枢纽的责任，近些年的集装箱吞吐量在世界范围内名列前茅，从2010年起到2018年，已经连续9年坐稳全球第一的宝座。

为更好地反映上海的集装箱运输市场水平，上海出口集装箱运价指数（SCFI）由此而生，通过分析运价指数的影响因素以及波动情况，可以更好地了解运输市场的价格趋势，控制价格水平，使集装箱运输市场平稳良好地发展，最大限度地发挥运价指数的指导性作用，为我国航运企业提出运价参考，增强上海在建设国际航运中心的竞争优势，乃至对于推动上海国际航运中心建设具有重大战略意义。

1.2 研究内容

本文的主要内容：第一章介绍了研究SCFI的背景，基于国内外对BDI，CCFI的研究现状，确定了本文的研究思路以及研究方法。第二章对研究所用到的理论基础进行陈述，介绍了单位根检验、ARIMA模型、ARCH模型。第三章展示收集到的2011年-2018年的相关数据，对数据本身进行基本的统计性描述，并初步进行处理。第四章应用ARIMA模型和ARCH模型对SCFI进行实证分析。最后对本文的研究成果进行总结以及对未来研究方向的展望。

2 理论基础

2.1 单位根检验

单位根检验是判断一组时间序列是否稳定，这个稳定的标准就是不存在单位根，单位根检验就是检验序列中是否存在单位根。

（1）DF检验

（2）ADF检验

在DF检验中，实际上是假定了时间序列是由具有白噪声随机误差项的一阶自回归过程AR（1）生成的。但在实际检验中，时间序列可能由更高階的自回归过程生成的，或者随机误差项并非是白噪声，为了保证DF检验中随机误差项的白噪声特性，Dicky和Fuller对DF检验进行了扩充，形成了ADF（Augment Dickey-Fuller）检验。

2.2 ARIMA模型简介

ARIMA（p，d，q）称为差分自回归移动平均模型，指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。p为自回归项，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。ARIMA模型定义如下：Φ（B）∨dXt=Θ（B）εt 其中Φ（B）为自回归系数多项式;Θ（B）为滑动平均系数多项式，∨为差分算子，B为滞后算子。ARIMA模型在经济预测过程中既考虑了经济现象在时间序列上的依存性，又考虑了随机波动的干扰性，对经济运行短期趋势的预测准确率较高，是近年应用比较广泛的方法之一。

2.3 ARCH模型简介

ARCH模型称为自回归条件异方差模型，主要用来描述金融数据的波动性（方差变化）。ARCH模型的基本思想是在以前的信息集下，某一时刻一个噪声的发生是服从正态分布的，该正态分布的均值为0，方差是一个随时间变化的量即为条件异方差，并且这个随时间变化的方差是过去有限项噪声值平方的线性组合即为自回归。这样就构成了自回归条件异方差（ARCH）模型。对于一个时间序列而言，在不同时刻可以利用的信息不同，而相应的条件异方差也不同，利用ARCH模型，可以刻画出随时间而变异的条件方差。

3 相关数据及处理

3.1 数据选取

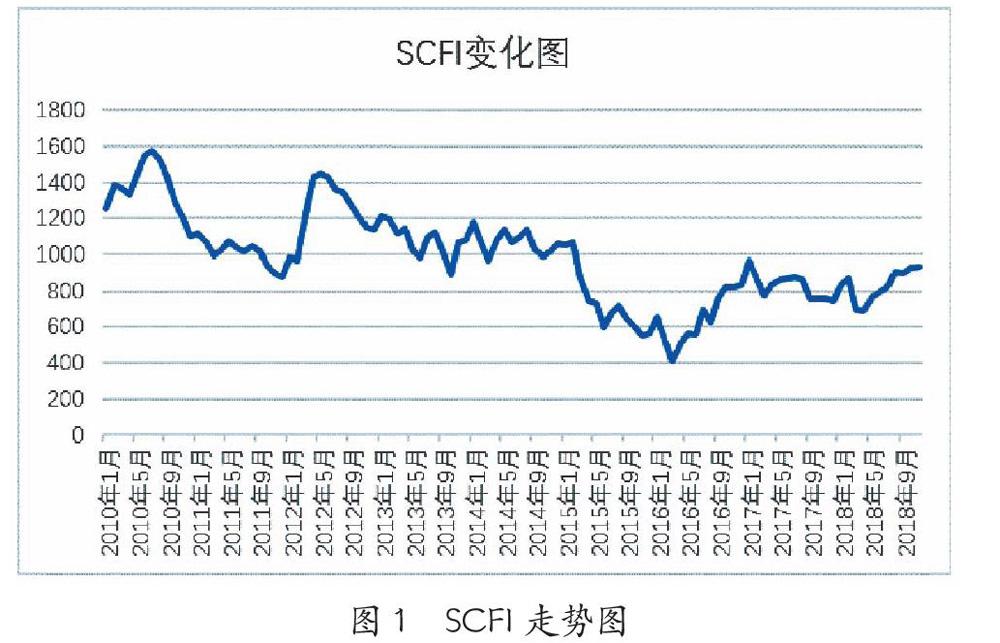
2009年10月16日，上海航运交易所推出新版上海出口集装箱运价指数，基期为1 000点。本文对上海出口集装箱运价指数取样做研究，时间上从2010年1月到2018年11月，数据来源于中华人民共和国交通运输部每月公布数据， 对这107个SCFI数据做图，具体走势如图1所示。从图1可知，SCFI指数呈不规则的锯齿波动，最高点将近1 600点，而最低点仅仅在400点附近，整体上可以看出波动幅度不小。

3.2 SCFI序列的单位根检验

由图1可以看出，SCFI序列不符合零均值同方差的特征，可以初步判断原时间序列是不平稳的，同时结合自相关系数图和单位根检验判断，可知自相关系数没有很快地衰减向零，不符合平稳性时间序列的特征。通过Eviews自带单位根检验可知检验统计值t=-2.887，大于显著性水平10%的临界值，所以不能拒绝原假设，序列存在单位根，序列是非平稳。

由于原序列的非平稳性，所以要对SCFI序列进行一阶差分，可知一阶差分后序列的自相关系数一阶后都显著落在置信区间内。单位根检验中t统计量值是-7.648，小于显著性水平为1%的临界值，表明至少可以在99%的置信水平下拒绝原假设，因此可以认为差分后的序列不存在单位根，序列是平稳的。

3.3 lnSCFI序列的单位根检验

3.3.1 lnSCFI序列的基本统计特征（见表1）

0.030725小于3，是瘦尾特征;偏度值小于0，是负偏态。J-B检验结果显示的概率为0.107大于0.05， 所以认为lnSCFI序列服从正态分布。从图2 lnSCFI的频数分布图中可以显著观察这些特征。

3.3.2 lnSCFI序列平稳性检验及处理

由图3可知，检验序列不存在一个明显偏离位置的随机变动，所以看作所检序列均值为0。但是，随着时间的增加，被检序列的波动趋势变大，因此存在时间趋势，在回归方程中加上时间趋势项。

ADF检验结果如表2所示，我们选择AIC评价和SC评价检验值最小的滞后项数，检验值相同时，选择滞后期最小的值，通过表3-2可知，滞后期为1时的AIC和SC最小，所以选择滞后一期。从表2可知，ADF检验值为-1.660755，大于显著水平为10%的临界值，接受原假设，所以lnSCFI存在单位根，是非平稳的。

4 实证分析

4.1 ARIMA模型建立

4.1.1 方程的识别、定阶

从一阶差分后的自相关函数图和偏自相關函数图4中可以看到，偏自相关系数和自相关系数在一阶时就都显著落在置信区间内，使得我们难以采用传统的自相关、偏自相关函数残差方差图、F检验、准则函数来确定模型的阶数。对于这种情况，通过反复对模型进行估计比较不同模型的变量对应参数的显著性以及AIC准则和SC准则来确定模型阶数。最后确定模型为ARIMA（2，1，2），对应的所有回归系数的显著性水平达到99%，其它试算模型的回归系数的显著性水平远不如该模型，同时该模型的AIC数值和SC数值是所有试算模型中最小的。综合考虑选定ARIMA（2，1，2）作为上海出口集装箱运价指数的均值预测方程。

4.1.2 模型拟合结果

由模型的系数的t统计量及其p值可知，模型所有解释变量的参数估计值在99%的显著性水平下都是显著的。模型建立后，可对模型拟合残差的效果图观测，观察波动的集群现象是否减弱或消除。从的图4模型残差分布图可知，序列的波动集群效应已减弱，不存在强的ARCH效应。

4.2 建立SCFI波动性的ARCH模型

4.2.1 lnSCFI的ARCH LM检验

为检验SCFI波动是否具有条件异方差，我们对ln（SCFIt）序列进行检验，所谓条件异方差是指预测数据与实际数据的误差常常会成群出现，在某一时期里相对地小，而在另一时期里相对地大，误差项的条件方差不是某个自变量的函数，而是随着时间的变化并且依赖于过去误差的大小。利用OLS （普通最小二乘法）进行估计得到由上面估计值可知此方程统计显著，拟合程度也很好，但观察其拟合方程的残差序列图5可看到有波动成群现象，这意味着序列ln（SCFIt）可能具有条件异方差性，所以上式进行ARCH LM检验。

得到的检验结果： 一阶ARCH效应的相伴概率为0.0036，小于0.05，拒绝原假设。说明残差序列存在ARCH效应，但不存在高阶ARCH效应。因此采用ARCH模型对式ln（SCFIt）=0.936849ln（SCFIt-1）+ut的随机扰动项建模以充分提取残差中的信息，使最终的模型残差成为白噪声。

4.2.2 模型结果

首先变量ln（SCFIt-1）的系数估计值近似为1，表明是单位根过程。然后，方差方程中ARCH项的系数为0.253<1，满足约束条件且P值为0.0447<0.05是统计显著的，Log likelihood对数似然值变大，AIC、SC变小，都证明ARCH（1，1）模型可以更好地拟合ln（SCFIt），反映lnSCFI的波动。

4.3 ARIMA模型预测结果

用拟合的有效模型ARIMA（2，1，2）的预测值与部分实际值对比得知模型的预测精度可行。并进行短期预测，得出2018年12月至2019年3月的预测值见表4-1。

根据预测结果显示上海出口集装箱运价指数将在未来5个月中有波动小幅度上涨，总体围绕925点上下波动，市场趋于稳定，与实际指数在2019年3月有较大偏差，说明模型对于短期的末期的描述并不充分，需要考虑其他影响因素的误差修正。

5 结论与展望

5.1 结论

通过使用计量经济学方法和Eviews软件操作，得出ARIMA（2，1，2）模型对上海出口集装箱运价指数时间序列的拟合效果较好，进行短期预测能有较高的预测精度，在不发生较大经济危机或突发事态的情况下，上海出口集装箱运输运价市场走向将在未来4个月中有波动小幅度上涨，总体围绕925点上下波动，接近基期1 000点的水平，相较于市场谷底来说，已经是大幅度回暖了。针对SCFI的波动性，对SCFI的对数序列进行分析和检验，最终得出ln（SCFIt）的一阶差分序列平稳，并且通过ARCH LM检验法对ln（SCFIt）误差项进行检验，结果表明具有一阶条件异方差性。这说明SCFI容易受到外界影响的干扰，比如经济发展情况，国际贸易情况以及行业相关政策的影响。使用ARCH （1，1） 可有效消除条件异方差，更好地拟合了SCFI的波动，有助于研究开发出针对上海出口集装箱运价的运费衍生品，为相关港航企业提供定价参考，为政府部门的决策调控提供帮助，助力上海国际航运中心的建设。

5.2 未来研究展望

由于模型自身和数据收集的局限性，只从时间序列本身的特性考虑，而没有考虑其他不确定因素的影响。虽然模型中是以随机项来反映这些不确定因素，但在预测期望值中其他不确定因素的影响是无法反映出来的。未来研究可以收集相关不确定因素的数据，来建立向量误差修正（VECM）模型对短期波动进行修正，使得模型的短期预测的效果更加良好。受到数据收集的限制，本文只采用了月度数据进行研究分析，未来研究可以使用周度数据来进行更加精确的分析，使得短期波动的状况更加贴合实际。

参考文献

[1] Cullinance K. A short-term adoptive forecasting model for BIFFEX speculation; a boxjenkins approach. Maritime Policy&Management.1992，2：91-114.

[2] Kavussanos M G， Alizadeh-M A H. Seasonality patterns in dry bulk shipping spot and time charter freight rates[J]. Transportation Research Part E： Logistics and Transportation Review， 2001， 37（6）： 443 -467.

[3] BERG-ANDREA SSEN JA. Some Properties of international maritime statistics[J].Mritime Policy&Management1996.（4）.381-395.

[4] George E.P.Box， Gwilym M. Jenkins， Gregory C. Reinsel.时间序列分析-预测与控制（原书第四版）[M].上海：机械工止出版社.2011.

[5] 陶长琪.计量经济学教程[M]上海：复旦大学出版社， 2012.

[6] 高铁梅.计量经济分析方法与建模：Eviews应用与实例（第二版）[M].北京：清华大學出版社，2006.

[7] 陈昭，刘巍，欧阳秋珍.计量经济学软件Eviews9.0简明操作教程[M].北京：中国人民大学出版社，2017.

[8] 赵国庆.经济分析中的时间序列模型[M].天津：南开大学出版社.2012.

[9] 蒋迪娜.我国出口集装箱运价指数研究[J].山西财经大学学报，2005，27（5）：90-94.

[10] 张小斐，田金方.基于ARIMA模型的短时序预测模型研究与应用[J].统计教育，2006，（10）：7-9.

[11] 朱玉华，赵刚.基于ARCH族模型的中国出口集装箱运价指数波动特征[J].上海海事大学学报，2013，（3）：48-52.

[12] 安潇潇.ARMA相关模型及其应用[D].哈尔滨.燕山大学.2008.

[13] 贺强.基于GARCH模型的国际干散货运价指数波动性研究[D].大连.大连海事大学，2013.

[14] 原云霄，王宝海.基于ARIMA模型对我国公路物流运价指数的预测[J].数学的实践与认知，2017，（23）：53-56.

[15] 李耀鼎，宗蓓华.波罗的海运价指数波动研究[J].上海海事大学学报，2007，27（4）：84-87.