基于PSO和GA混合优化SVM的水质评价
2019-06-28聂笃宪魏伟康庄泽鸿吴海童卜加慧
聂笃宪,魏伟康,庄泽鸿,吴海童,卜加慧
(华南农业大学 数学与信息学院,广州510642)
传统的水质评价方法多参照水质类别标准,基于多元统计[1-2]对常规的几种水资源污染因子进行权重计算,建立综合评价指标。该方法操作简单,得到了广泛应用,但却未能解决水质评价中污染物的不确定性与非线性[3]。随着人工智能技术的发展,BP神经网络[4]、支持向量机[5]与决策树[6]等方法逐渐被应用于水质评价中,且取得了不错效果。但这些方法都存在着不足,BP神经网络要求大量的样本数据提高分类准确率,且容易陷入局部极小值;SVM对参数选取具有盲目性,即求得的预测模型不是最优解;决策树对于不均衡的水质样本数据,信息增益会偏向于那些更多数值的特征,从而产生过拟合。因此,许多学者采取了粒子群优化PSO、遗传算法GA等优化水质评价模型参数,并取得了一定成果。如郭建青等[7]将PSO算法应用于估计河流水质参数的函数优化问题,提高了运算过程的收敛性;王冬生等[8]用PSO算法训练RBF神经网络,提高了水质评价精度。
本文利用基于PSO算法和遗传算法GA的混合算法HPSOCS搜寻SVM训练的最优参数,从而降低了SVM对参数选择的盲目性,并将改进的HPSOCSSVM算法应用于山东省菏泽市水质评价中,实验结果表明,HPSOCS算法提高了水质评价模型分类的准确度,评价效果更优,体现了该优化算法良好的性能。
1 基于HPSOCS的支持向量机方法
1.1 支持向量机
支持向量机SVM的基本原理是结构风险最小化,思路是在样本空间中,找到一个最优超平面将样本空间分成两类,使得被分成两类的样本集与最优超平面的距离最大。在使用支持向量机之前,先把分类问题分成两种,一种是线性可分,另一种是线性不可分。
1.1.1 解决线性可分问题
设样本集为(xi,yi),i=1,2,…,n;其中yi={+1,-1}是类别符号,利用分类面将样本正确地分成两类,且令分类间隔最大,也就是使‖w‖2最小(w为分类面的法向量),其中分类面的方程为:
w·x+b=0
而想要分类面在对所有样本进行分类时不出现错误,就要满足以下条件:
yi[w·x+b]-1≥0,i=1,2,3,...,n
满足以上条件和令‖w‖达到最小的分类面就是得到的最优分类面。
1.1.2 解决线性不可分问题
引入松弛变量,同时增加核函数K(x,xj)和惩罚因子c来进行分析,将低维空间的输入数据通过非线性变换转换成高维空间,使之成为线性样本,从而求出最优分类超平面。
求解超平面转换为最优化问题为:
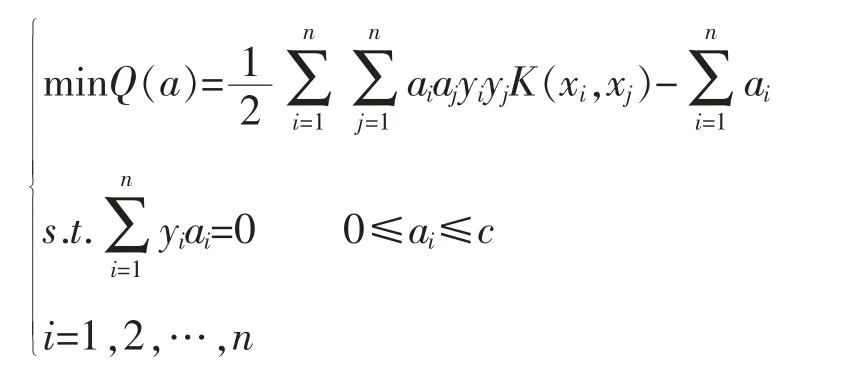
本文选取RBF径向基核函数K(x,xj)=exp(-||x-xj||2)/2g,其中,g为核函数参数。
判别函数为:
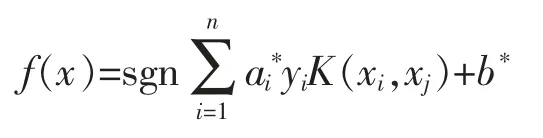
通过推导过程看出,核函数参数g和惩罚因子c的选取对SVM的分类性能至关重要,因此本文用基于粒子群优化算法和遗传算法的混合算法来优化SVM参数。
1.2 基于粒子群优化和遗传算法的混合算法概述
粒子群优化是一种模拟鸟群捕食行为的群体智能演化算法[9],该算法的基本步骤为:初始化粒子群的规模X={x1,x2,…,xn}与每个粒子的位置Xi=(xi1,xi2,…,xiD)T和速度Vi=(vi1,vi2,…,viD)T。在每一次迭代中,计算每个粒子的适应度,通过个体极值(pbest)与全局极值(gbest)来更新每一个粒子的位置和速度,当达到寻优条件时即退出迭代。
位置、速度更新方程为:

遗传算法GA 是由Holland 提出的一种进化计算模型[10],包括选择、交叉和变异等遗传操作。GA算法已被广泛用于函数优化、机器学习、智能控制、模式识别等许多领域。
遗传算法和粒子群优化算法各有自身的优势和某些不足,许多学者结合两者的优势做了大量研究工作[11-12],本文采用文献[12]中提出的HPSOCS算法对SVM参数进行优化。在HPSOCS算法中,将交叉和选择操作引用到PSO算法中,构造一种结合PSO和GA的混合优化算法。
1.3 基于HPSOCS改进的支持向量机
利用SVM进行训练测试时,核函数参数g和惩罚因子c的选取对模型的泛化能力影响较大。目前常用的SVM 参数寻优方法为基于交叉验证(Cross Validation)下的网格搜索法(grid search)。本文将基于粒子群优化和遗传算法的混合算法与支持向量机结合,对其参数进行优化。采用默认的RBF核函数,动态设置参数c和参数g(RBF核函数中的方差),分别作为粒子的位置坐标。适应度函数为支持向量机对样本数据训练的分类准确率,即在每一次迭代过程中,通过更新参数计算分类准确率,即构造出基于混合算法的支持向量机。
改进的支持向量机算法流程如图1。
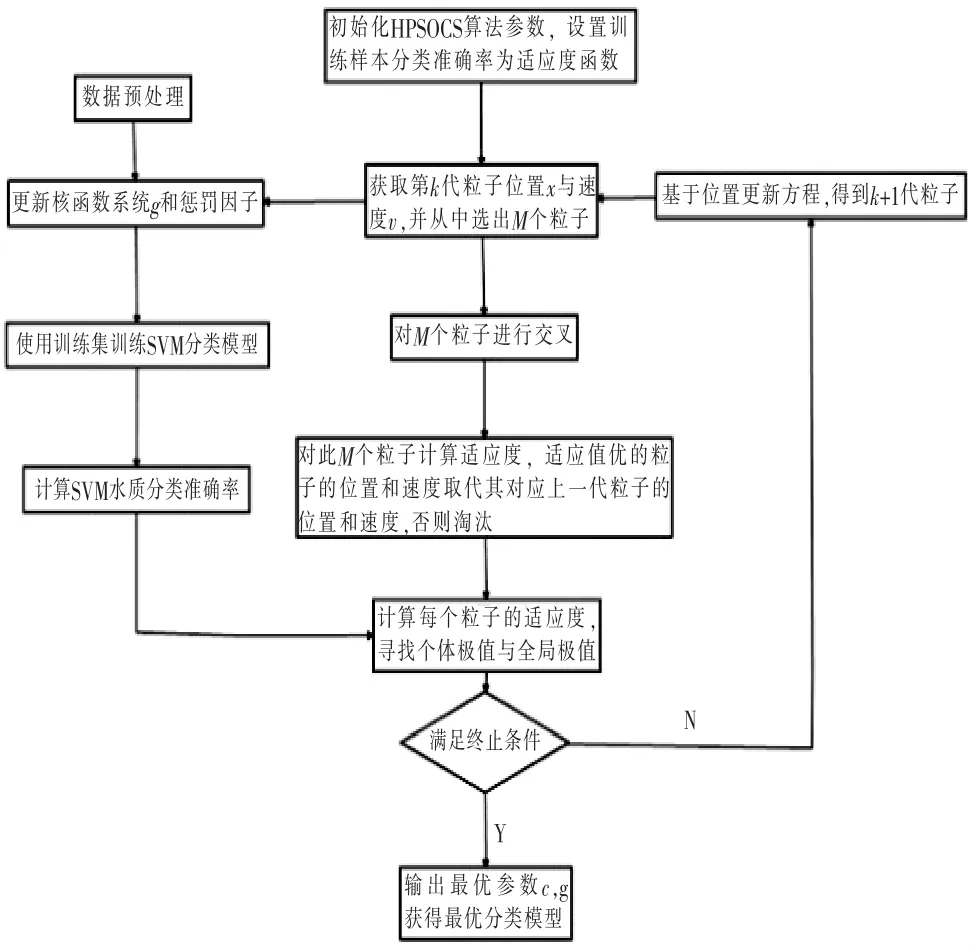
图1 HPSOCS-SVM算法流程
2 数据来源与预处理
本文研究数据来自广州某环境监测技术公司提供的山东省菏泽市10个水质自动监测站的监测数据,采样时间为2018年4月6日至4月27日。根据GB 3838—2002《地表水环境质量标准》,本次评价将溶解氧DO、高锰酸盐、化学需氧量COD、氨氮NH3-N、总磷TP纳入评价体系,依据标准进行水质评价分级,如表1。

表1 地表水环境质量分级标准 单位:mg/L
先对原数据进行Z-score标准化后,剔除z分数大于3的异常数据,再用Matlab对数据进行mapminmax归一化处理,消除污染物量纲及浓度不同带来的影响,从而得到最终的实验数据。
3 基于HPSOCS-SVM算法水质评价模型构建与求解结果
本文从预处理后的数据中抽取729作为训练集,剩余131作为测试集。将训练集代入支持向量机中训练并用混合算法优化参数,得到分类准确率最高的参数,模型参数优化选择。由于该SVM 模型属于非线性分类,需要确定惩罚因子c 和核参数g。文中HPSOCS-SVM模型参数初始化为c和核参数g的HPSOCS搜索区间范围分别设为[0.1,100]和[0.1,10];种群规模20;最大迭代次数为200;c1=1.5,c2=1.7。支持向量机和HPSOCS算法均采用MATLAB编程计算。最终迭代寻优得到最优参数为:c=173.0571,g=1.2779。
将参数优化后的HPSOCS-SVM算法应用于测试集,得到结果如图2(a),其分类准确率达到95.3%,说明其准确率高,能够应用于水质评价中。
为了比较HPSOCS-SVM算法的优劣,在相同数据集下,本文还分别建立了SVM模型、BP神经网络模型和PSO-SVM模型,并对求解结果进行比较。比较结果分别如图2(a),图2(b),图3(a),图3(b),执行效率比较如表2。

图2 HPSOCS-SVM和PSO-SVM分类结果

图3 传统SVM分类和BP神经网络分类结果

表2 不同模型分类准确率与效率比较
由图2,图3及表2对比可看出,优化效果HPSOCS-SVM算法最好,其次是PSO-SVM算法,BP神经网络介于PSO-SVM与SVM之间;而执行效率HPSOCS-SVM算法耗时明显增大,当数据量较大时,HPSOCS-SVM算法耗时明显增大。利用BP神经网络建立的水质分类模型要求大量的数据进行训练才能提高模型分类的准确度,而水质评价三级的数据太少而导致三级分类准确率低,且神经网络也存在容易陷入局部极小点、权重和阀值的选取比较困难等问题。
HPSOCS-SVM模型相比于PSO-SVM模型,充分利用了粒子群优化和遗传算法的优势,混合算法具有更强的参数寻优能力,同时克服了SVM对于参数选择的盲目性,得到了更加精确的模型参数,使得分类结果更加精确,说明HPSOCS混合算法优化SVM参数的有效性,能够应用于水质评价中。
4 结语
(1)以山东省菏泽市2018年4月6日至4月27日间860组水质监测数据为实验对象,基于PSO和GA的混合算法(HPSOCS)优化支持向量机模型参数并构建了水质评价模型,与PSO、BP神经网络和传统的SVM算法相对比,该方法具有更高的水质分类准确率。
(2)由于HPSOCS优化支持向量机收敛准确率高、效果好,具有较好的推广性,可广泛应用于水体质量的评估,为水资源的防控治理提供科学的理论依据。
