长江上游兰家沱至温中坝航道潜能提升初探

龙 浩，李文杰，2，陈 川，戴 卓,戴佳伶

(1.重庆交通大学水利水运工程教育部重点实验室，重庆 400074；2.重庆交通大学国家内河航道整治工程技术研究中心，重庆 400074)

长江上游地区是西部大开发重点区域，蕴藏着巨大开发投资潜力。长江上游航运在矿建材料、危化品、集装箱等大宗长距离运输市场中具有广阔前景。兰家沱至温中坝河段(上游航道里程737—806 km)作为长江上游干流重要组成部分，起着承上启下的重要作用。而目前该河段枯水期航道维护尺度仅为2.7 m×50 m×560 m(水深×航宽×弯曲半径)，为内河Ⅲ级航道通航标准，与长江上游地区日益增长的水运需求存在较大差距[1]。

当前，长江上游重庆至宜宾段Ⅱ级航道建设工程正处于论证阶段，评估上游航道天然状态下可提升潜力以期为长江航道资源高效利用、长江上游航道建设标准提供科学依据，合理评估航道资源的开发潜能也是摆在决策者面前的重要课题。鉴于此，本文以长江上游兰家沱至温中坝河段为例，基于优良河段及河相关系理论，分析和建立了兰家沱至温中坝河段河相关系式，初步估算本河段航道可提升潜能。

1 航道潜能理论计算分析

航道潜能理论计算多为经验公式，结合理论探讨较少。前苏联文献曾率先提出了天然状态下航道水深的估算方法，中国相关研究人员在此基础上总结相关经验公式并提出自然河流通过航道整治等手段改进后航道能到达的水深公式[2]，见式(1)。

(1)

式中h0——航道保证水深；K1、K2——经验性航道特性系数；Q0——最低通航保证流量；S——枯水期河道水面比降。

该公式在长江、西江等代表性河流的相关整治工程中得到验证。与之前航道潜能或可开发改善程度纯粹依靠数学模型或河工模型进行推演论证相比，此公式可对航道可开发水深程度初步估算，使传统的航道建设论证思路得到拓展。但尚存问题是此式中系数和指数均为经验值，未能将具体的河道断面信息加以考虑。以长江为例，其上游为山区河流而中下游为平原河流，河道断面差距悬殊，开发论证的角度截然不同，故本式缺乏应用到实际河道工程中的理论依据。

随着水力学及河流动力学学科的快速发展，相关学者针对航道水深估算问题提出了“稳定航深估算法”，该方法运用航道整治工程技术中确定整治线宽度的思路，将河流动力学和相关系理论引入其中，使之遵循了河流本身特性又符合河流学科理论原理，目前该方法已在西江等流域的建设规划中得到应用且效果较好[3]。稳定航深估算法需先确定天然河道的优良河段，优良河段可认为是航道整治工程参考的样板，是天然河流中对航行没有障碍的河段，而优良河段的河相关系意在描述天然状态下河流通过整治后达到的最合适的河床断面形态。在传统的航道整治工程断面设计中也常采用优良河段的模拟方法，此方法可作为预测河道变形和河道整治工程规划的依据[4]。在确认优良河段之后，可先假定航道在完成整治后的河道断面与优良河段的断面形态相似，以此假设建立某一特征流量(一般为设计最低通航保证流量)下的优良河段河相关系，据此关系可推导航道可开发的最大稳定航深计算式式(2)[5]。利用理论稳定航深值与标准内河航道等级的航深对比，即可判定河道可开发航道尺度。本文采用稳定航深估算法推求长江上游兰家沱至温中坝河段在设计最低通航保证流量下能达到的稳定航深。

(2)

式中h1——理论稳定航深值；H——河道断面平均水深；n——特征流量下河床糙率；Q——某一特征流量；J——特征流量下水面平均比降；α、β、η——河相关系系数(由河床断面数据拟合得到)。

此外，本文还采用等级流量比较法验证，等级流量比较法是在给定标准航道尺度条件下对比计算理论需求流量与天然实际流量，判定航道在天然条件能否达到某一个等级，见式(3)[6]：

(3)

式中Q——达到某等级航道理论需求流量；ζ——断面修正系数；i——国家内河标准航道等级；bi——i级标准航宽；hi——i级航道维护水深；J——枯水期水面平均比降；n——枯水河床糙率。

通过稳定航深估算及等级流量比较判定，可初步估算本河段的航道开发潜能及航道建设尺度。

2 兰家沱至温中坝优良河段河相关系

2.1 优良河段河相关系

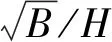
(4)

式中B——水面河宽;H——河道断面平均水深;α、β——待定系数及指数。

上文式(2)中河相关系系数α、β即是基于式(4)统计分析得到，此式只取决于断面的宏观形态，不过多考虑断面细节，因而在航道规划设计领域应用范围较广，部分应用实例见表1。本文采用式(4)对本河段河流沿程宽深相关关系进行描述。

表1 部分优良河段河相关系式实例

兰家沱至温中坝河段位于长江上游叙渝段重庆江津以上(图1)。该河段地处于丘陵地带，河床大多由基岩、卵石或卵石夹沙组成，本河段滩险较少且分布稀疏，区间内水流条件大致稳定，河段整体可视为无需治理的优良河段。

图1 长江上游兰家沱至温中坝区位

据长江上游实测枯水期航道地形图(来源：长江航道局，P=98%，设计最低通航水位)，选择本河段区间图绘制62个代表性断面，部分典型横断面见图2。取零上水位时自然河宽B，零下水位过水断面面积A和断面平均水深H。经统计，本河段河宽大致在300～700 m之间，平均水深在2～15 m之间(图3)。

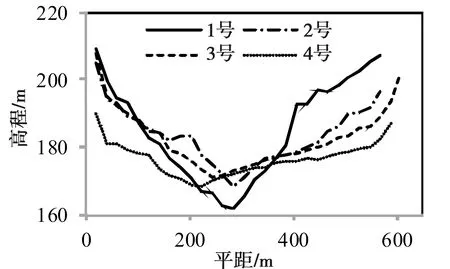
图2 兰温段典型横断面

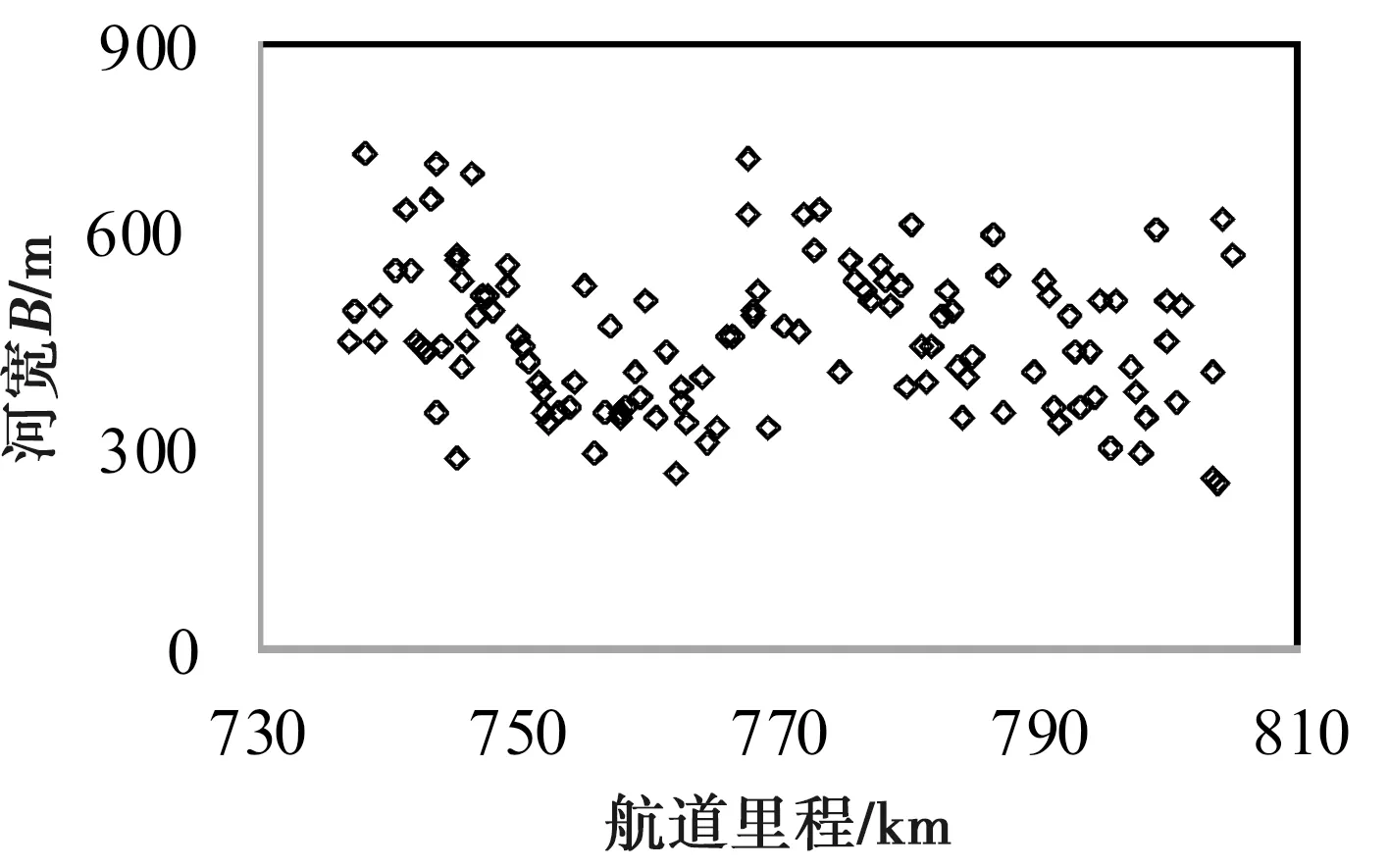
a)沿程断面河宽(B)分布

b)沿程断面平均水深(H)分布

其中R2为相关性系数，表示估算值与实际值间的关联程度，该值愈靠近1，表征数据间相关程度越高，拟合结果也更可靠。根据结果，α=27.489，β=-1.194，由此得到兰温段沿程河相关系式：

图4 兰温段沿程河相关系曲线

(5)

长江干线基本水位站朱沱站坐落于温中坝上游处，本文以朱沱站水位流量为基础估算资料，朱沱站近年设计最低通航保证流量为2 230 m3/s(P=98%)，区间段无大型支流入汇，最大汇入设计流量不到90 m3/s(P=98%)，即支流的汇入对本区间段河道形态的影响非常小，可视为全程河段河相关系基本一致，即仅需在区间段建立完整河相关系，无需分区段处理。

2.2 航道水深计算关系

在航道整治工程的断面设计确定整治线宽度工作中，通常认为设计最低通航保证流量下的河道断面与认定的优良河段断面相似，然后利用标准航道宽度对应的边缘水深h与断面平均水深H线性拟合得到水深改正系数，用以计算通过整治后航道在标准水深下的整治线宽度[10]。一般天然河流都存在H～h的相关关系，人工明渠线性关系更为明显，将此关系可转换成函数关系H=ηh形式，其中η为待定系数项，可通过数据整理后点绘H～h相关线拟合得到η值。据国内大量河道断面数据调查统计，中国河流η区间值一般在0.6～0.9之间，平原河流相比山区河流会更大一些。

依照长江干线标准内河航道等级及对应船型划分，I-6级标准航道维护水深为3.5～4.0 m，II级标准航道维护水深2.6～3.5 m。本文以当前论证的3.5 m航道建设工程为基准，建议本河段航道建设标准为：Ⅱ级标准3.5 m×100 m×800 m，Ⅰ级标准为3.5 m×110 m×800 m。

统计分析本河段在设计最低通航保证流量(98%)下河道各断面平均水深H，Ⅰ、Ⅱ级标准航道尺度下不同航宽对应的边缘水深h，绘制H～h相关线(图5)。通过线性拟合，得到待定系数η及相关性方程(表2)。

表2 标准建设尺度下兰温段水深相关关系

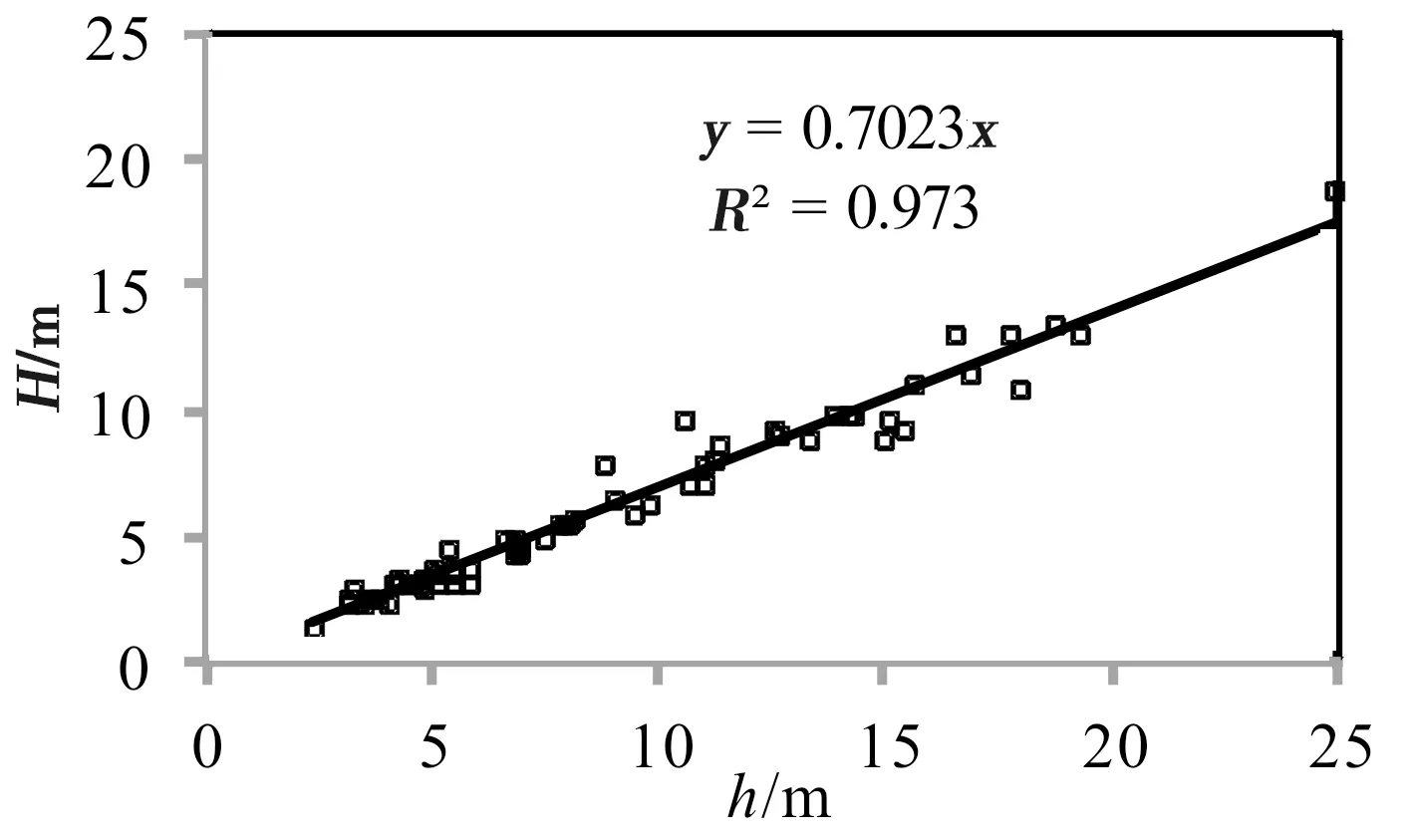
a)H与h相关关系(P=98%、Ⅰ级)

b)H与h相关关系(P=98%、Ⅱ级)图5 兰温段沿程H～h相关线

3 兰家沱至温中坝段航道潜能估算

3.1 已知条件

据长江航道局等有关部门的实际勘察数据，长江上游兰家沱至温中坝河段设计最低通航保证流量(P=98%)为2 230 m3/s，水面平均比降0.26‰，河床糙率n在0.030～0.045之间。

3.2 稳定航深法估算

本河段河道弯曲程度适中，且沿程宽度大都超过300 m，理论通航条件优越。依托 “稳定航深估算法”，结合前文拟合产生的河相关系参数，可计算本河段在设计最低通航保证流量(P=98%)下的航道开发潜力，即Ⅰ、Ⅱ级标准航道尺度下的稳定水深。本文取3组河床糙率值进行试算，分析糙率值对理论稳定航深计算值的影响程度，不同糙率值对应的理论稳定航深见表3。

表3 设计最低通航流量(P=98%)兰温段不同糙率值对应理论稳定航深计算值

由表3可得，理论稳定航深计算值随糙率值的增大而增大，且糙率值影响程度较为敏感。在Ⅰ级航道标准下，糙率值自0.030增至0.045，理论稳定航深计算值增加37.4%；Ⅱ级航道标准下，糙率值自0.030增至0.045，理论稳定航深计算值增加37.5%。本文以糙率0.030为准则保守估算，得到本河段在Ⅱ级航道标准下的最大稳定航深为5.46 m，Ⅰ级航道的最大稳定航深为5.39 m。

3.3 等级流量法判定

本文拟定的Ⅰ、Ⅱ级航道标准最低维护水深为3.5 m，航宽110、100 m，糙率值取0.030，ζ为断面修正系数，由水深修正系数和河宽改正系数决定，据断面实测资料得到Ⅰ级航道标准下ζ值为3.09，Ⅱ级航道标准下ζ值为3.14，用等级流量法判定实际流量是否满足本河段达到需求航道标准的理论流量，理论需求流量计算值见表4。

表4 兰温段在Ⅰ、Ⅱ级航道建设标准下的理论需求流量

由表4可得，当糙率值取0.030时，建成Ⅱ级航道理论需求流量为1 360 m3/s，Ⅰ级航道理论需求流量为1 473 m3/s，均小于本河段设计最低通航保证流量(P=98%)，说明本河段航道经整治措施后可达到Ⅰ级内河航道建设标准(3.5 m×110 m×800 m)。

4 结论

本文采用优良河段河相关系理论，结合长江上游兰家沱至温中坝河段实际参数，运用稳定航深估算与等级流量判定的方法均表明本河段具备开发至内河航道建设标准Ⅰ级的潜力。但值得注意的是，长江上游的实际航道条件复杂，控制因素众多，如尚存的诸多单线航道、水流条件差的典型河段以及生态制约河段都需通过实地调研取证分析。因此，本文方法的优点在于计算简易，较为方便，仅可供航道开发初期选址或论证提供参考，实际工程的准确性有待数学模型及河工物理模型试验进一步验证。