求解一维对流方程的高精度紧致差分格式

侯波,葛永斌

(宁夏大学数学统计学院,宁夏 银川750021)

1.引言

对流方程在生物数学、能源开发、空气动力学等许多领域都具有十分广泛的应用,因此求解该类方程具有非常重要的理论价值和实际意义.然而,由于实际问题通常十分复杂,往往难以求得精确解,因此研究其精确稳定的数值解法是十分必要的.

针对对流方程国内外很多学者提出了很多的数值方法.如张天德和孙传灼[1]针对一维对流方程采用待定系数法,得到了两层四点格式和四阶六点格式,并且是无条件稳定的,该方法适用于在点数确定的前提下,得到精度高的差分格式; 于志玲和朱少红[2]针对一维问题建立了中间层为两个节点的三层显格式,其截断误差为O(τ2+h2); 曾文平[3]针对一维对流方程推导出了一种两层半显式格式，其截断误差为O(τ2+h2),该格式是无条件稳定的.姚朝辉等人[5]将二阶的迎风格式和中心差分格式进行加权得到了WSUC格式,该格式是无条件稳定的;但该格式时间方向和空间方向仅有二阶精度.汤寒松等人[6]通过立方插值拟质点方法(CIP 方法),给出了一些保单调的CIP格式; Erdogan[9]针对一维的对流方程推导出了一种指数拟合的差分格式,其截断误差为O(τ2+h2); Bourchtein[10]构造了对流方程的三层五点中心型蛙跳格式,该格式的截断误差为O(τ4+h4); 即该格式时间和空间均具有四阶精度,但是该格式是三层的,空间方向需要五个点,并且是条件稳定的; Kim[11]构造了多层无耗散的迎风蛙跳格式,即时间和空间分别具有二阶、四阶、六阶精度,但格式为三层甚至是四层的,并且六阶格式空间方向最多需要五个点,给靠近边界的内点的计算带来困难.

综上所述,文献中已经有的数值计算方法大多为低阶精度的,而高精度方法涉及多个时间层,需要一个或多个时间启动步,或者空间方向的网格节点多于三个,这都给计算造成困难或不便.为此本文将构造一种紧致格式,这里紧致格式的定义为对时间导数项的离散采用不超过三个时间层,而对空间导数项的离散采用不超过三个网格点,时间和空间即可以达到高阶精度（三阶及三阶以上）的格式.本文拟构造的格式时间方向仅用到两个时间层上的函数值,在每个时间层上仅涉及到三个空间网格点,格式时间和空间具有整体的四阶精度.该格式的优点是无须启动步的计算,并且在对靠近边界点的计算时,不会用到计算域以外的网格节点.此外该格式为无条件稳定的,可以采用比较大的时间步长进行计算.最后通过数值实验验证本文格式的精确性和稳定性.

2.差分格式的建立

考虑如下一维对流方程：

给定初始条件为:

给定周期性边界条件为:

其中,u(x,t)为未知函数,f为非齐次项,a为对流项系数,φ(x)为已知函数.

将求解区域[b,c]等距剖分为N个子区间：b=x0,x1,··· ,xN−1,xN=c,并且定义时间也采用等距剖分,步长用τ表示.在本文中,我们利用分别表示u在(xi,tn),点处的函数值.

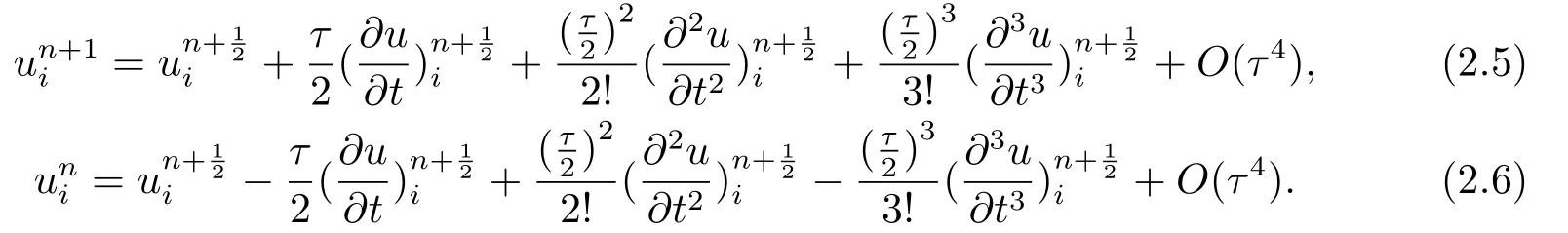
其中

同理可得:

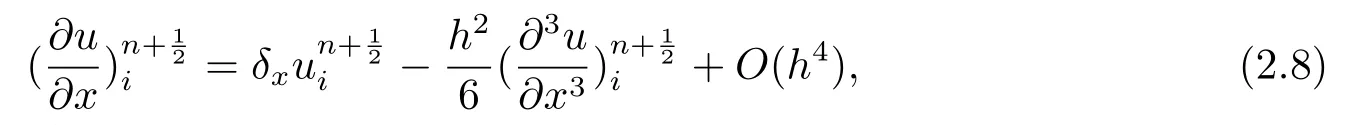
将(2.7)和(2.8)代入(2.4)整理可得:

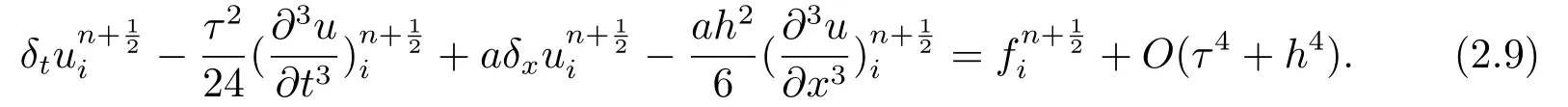
为了使该格式在时间方向和空间方向上均达到四阶精度,须对(2.9)式中的项进行二阶的离散,同时为了保证本文格式的紧致性,即空间方向不超过三个网格点,我们对(2.1)式进行如下变形:

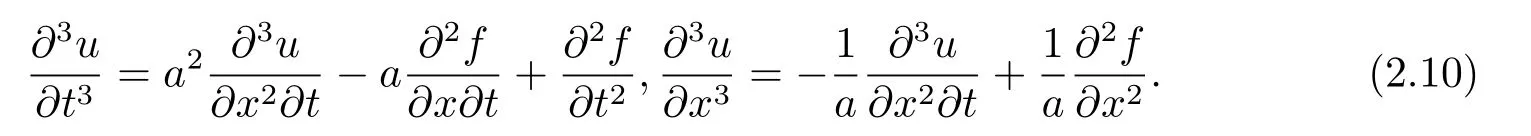
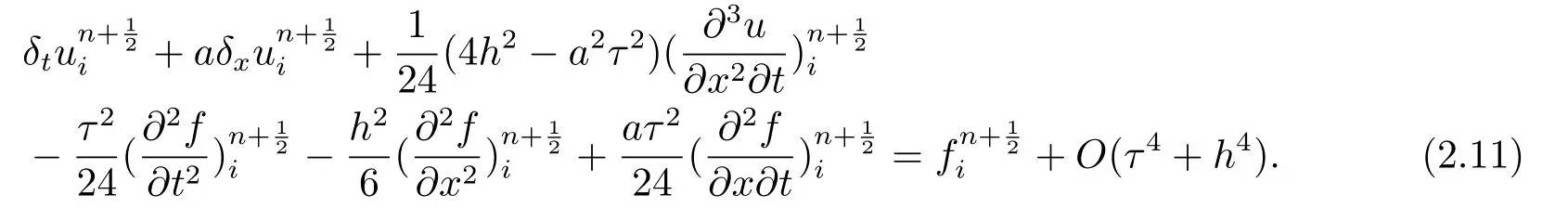
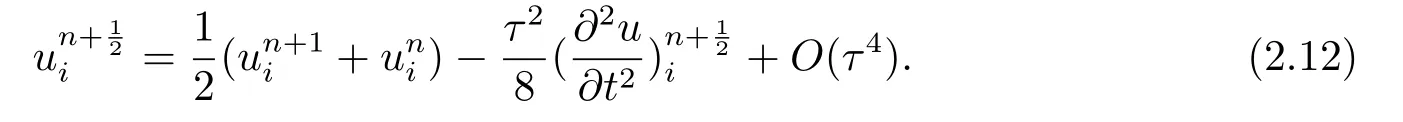
从而可得:

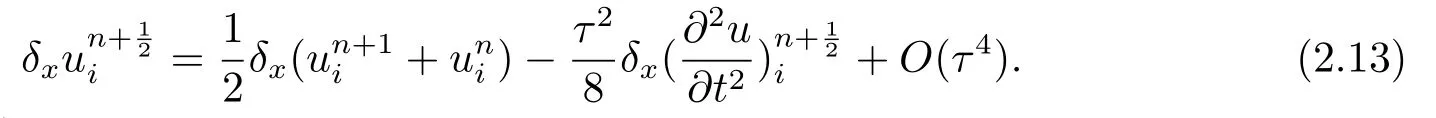
将(2.13)代入(2.11)得:

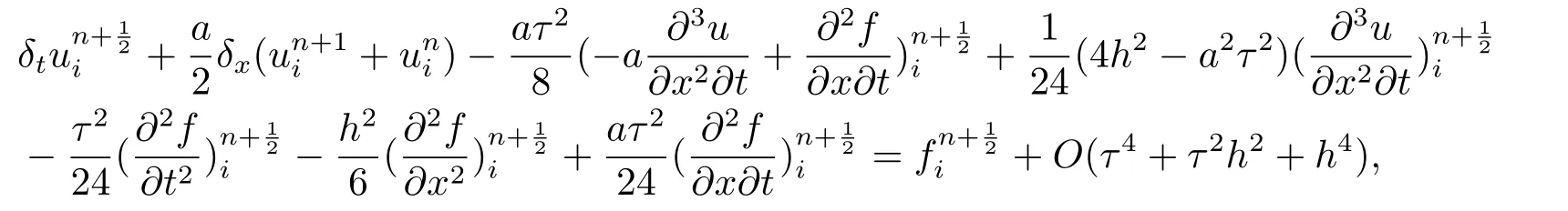
即,

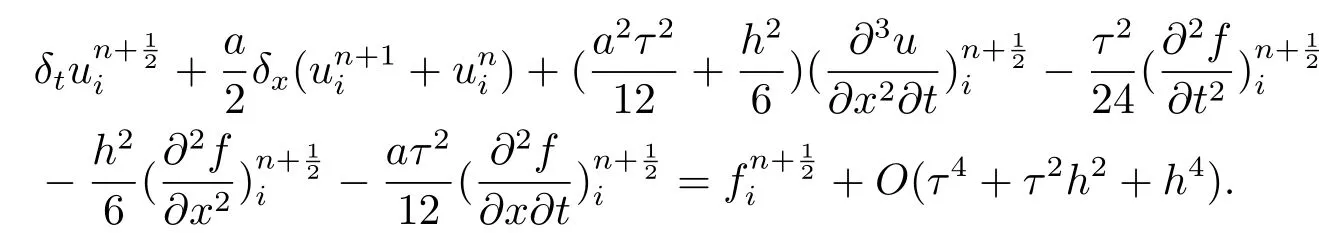
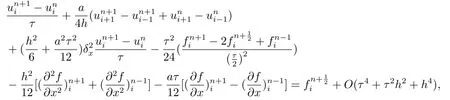
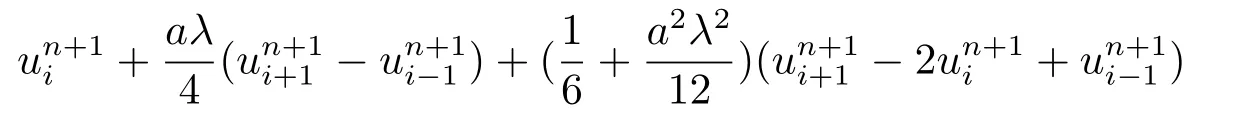
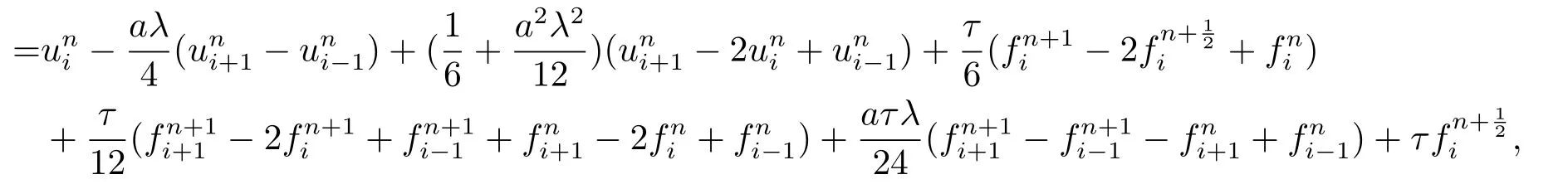
即,

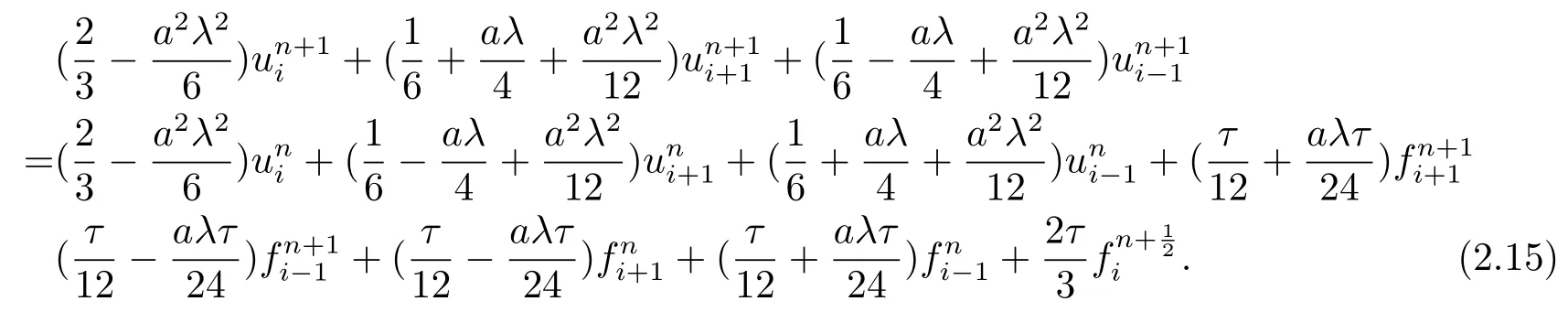
由推导过程可知,该格式的截断误差为O(τ4+τ2h2+h4),即格式(2.15) 在时间和空间上均可达到四阶精度.我们注意到,格式为两层格式,并且格式每层仅用到三个网格点,形成的代数方程组系数矩阵为循环三对角矩阵,可采用追赶法进行求解[8],同时由于要求未知时间层上(第n+1层)中间点的系数不能等于0,即因此

3.稳定性分析

下面采用von Neumann方法分析本文所推导的差分格式(2.15)的稳定性.

对于(2.15)式,舍掉非齐次项f,即假设f项精确成立,令uni=ηneIσxi,其中,η为振幅,σ为波数,为虚数单位,有

两边同时约掉eIσxi,并整理可得：

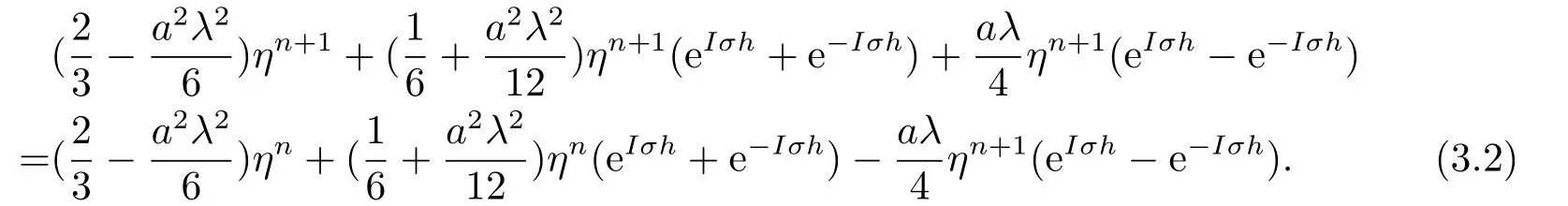
利用Euler公式,即eIσh=cosσh+Isinσh,e−Iσh=cosσh −Isinσh,可得:

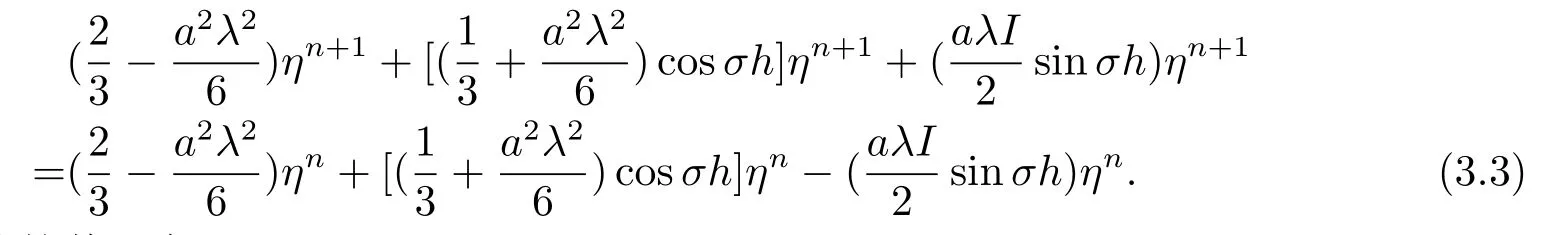
对上式进行化简整理有

从而可得格式(2.15)的误差放大因子为:

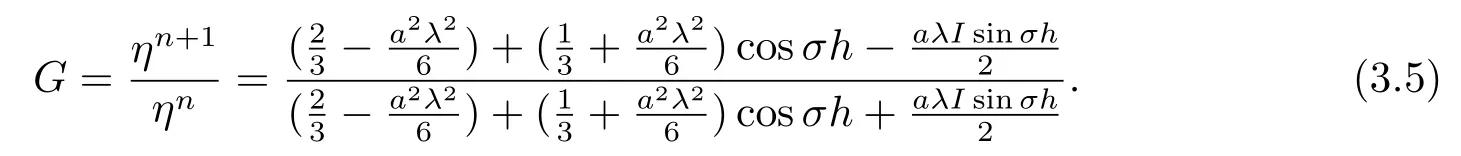
由von Numann稳定性定理可知当|G| ≤1 时,格式是稳定的,由(3.5) 可得|G|=1,因此,格式(2.15) 是无条件稳定的.

4.数值实验

为了验证本文格式(2.15)的精确性和稳定性,现考虑以下三个具有精确解的初边值问题.分别采用Crank-Nicolson(C-N)格式,文[7] 中格式和本文格式(2.15) 进行计算; 其中,最大绝对误差及收敛阶的定义为:

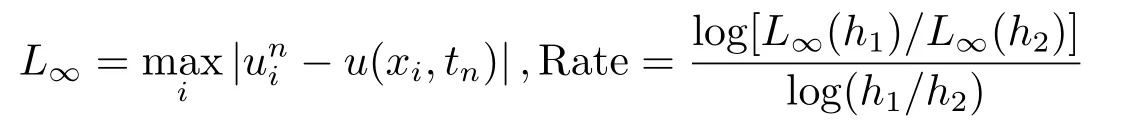
L∞(h1)和L∞(h2) 为空间网格步长分别为h1和h2时的最大绝对误差.

问题1[7]:

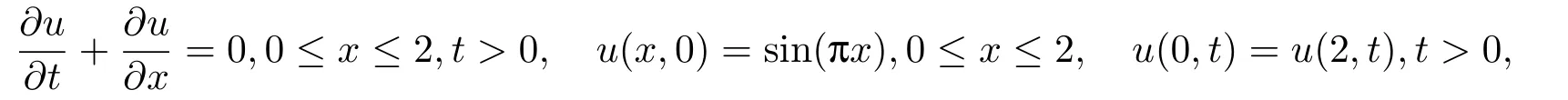
该问题的精确解为:u(x,t)=sin[π(x −t)].

表1 问题1 当λ=τ/h=0.5,t=1 时刻的最大绝对误差及收敛阶

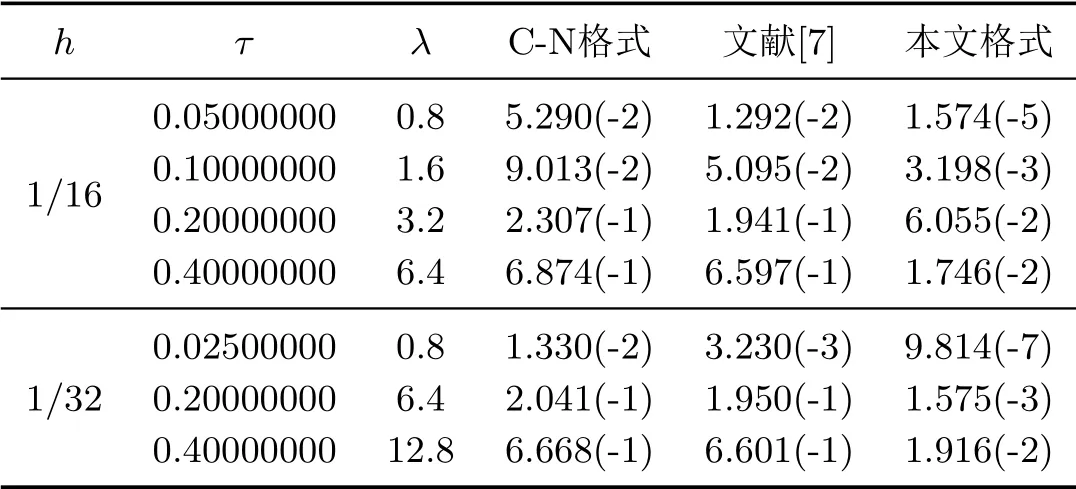
表2 问题1 当τ=λh,t=2 时刻的最大绝对误差

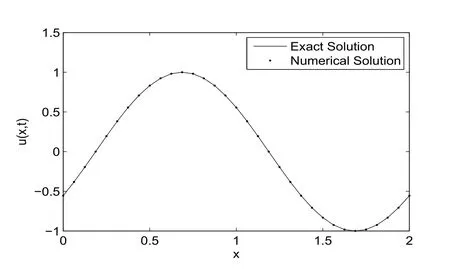
图1 问题1 当N=32,τ=0.03125,t=0.2 时刻的数值解与精确解

表1给出了针对问题1三种格式在不同空间步长h下,当λ=τ/h=0.5,t=1时的最大绝对误差和收敛阶.我们发现C-N格式在时间和空间上都为二阶精度,由于文[7]格式时间具有二阶精度,空间具有四阶精度,因此当取τ=O(h) 时,格式空间仅有二阶精度,而本文格式时间和空间均为四阶精度.图1给出N=32,τ=0.03125,t=0.2数值解与精确解对比图,可以看出数值解与精确解吻合的很好.

表2给出了当h=1/16和h=1/32时,τ=λh,t=2时刻对问题1采用三种格式计算的最大绝对误差.可以看出网格比λ最大取到12.8,计算仍然是稳定的,因此本文格式是无条件稳定的.并且本文格式在所有参数下,其计算结果比C-N 格式和文[7]格式计算结果更加精确.

问题2[7]:

该问题的精确解为:u(x,t)=ecos[π(x−t)].

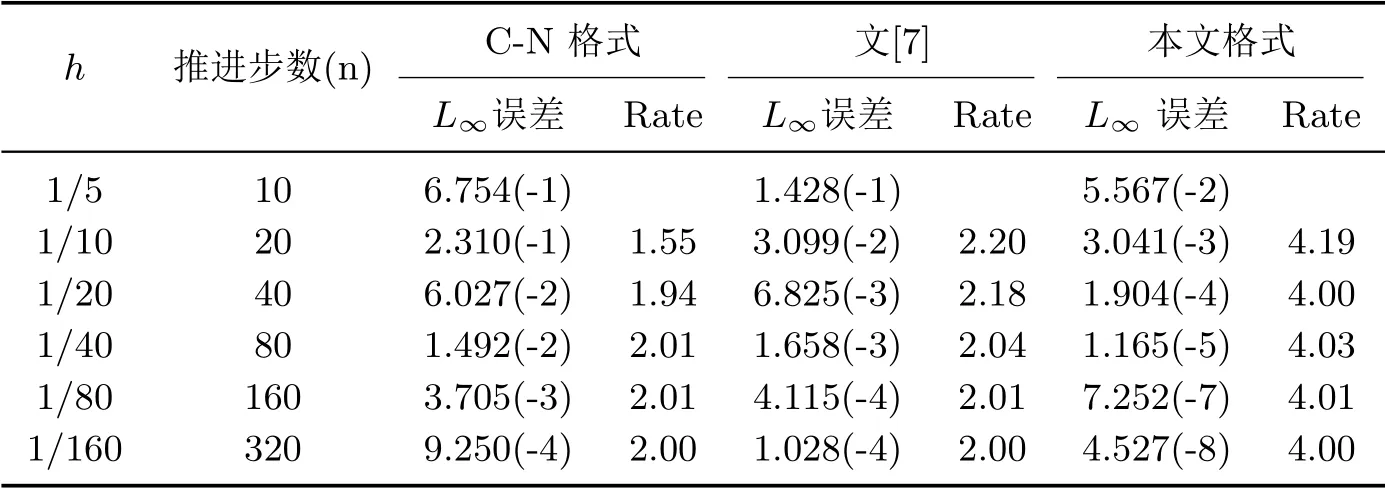
表3 问题2 当λ=τ/h=0.5,t=1 时刻的最大绝对误差及收敛阶

表4 问题2 当τ=λh,t=2 时刻的最大绝对误差

表3和表4给出了针对问题2利用本文格式和C-N格式以及文[7]格式的计算结果.表3考察了格式的精度,表4验证了格式的稳定性.可以看出本文格式在时间和空间上均可达到四阶精度,并且是无条件稳定的.

问题3

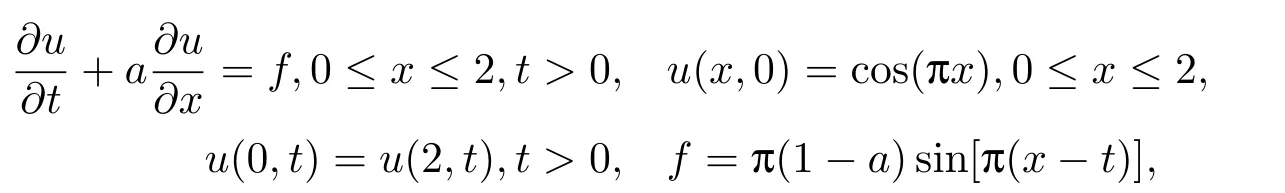
该问题的精确解为:u(x,t)=cos[π(x −t)].

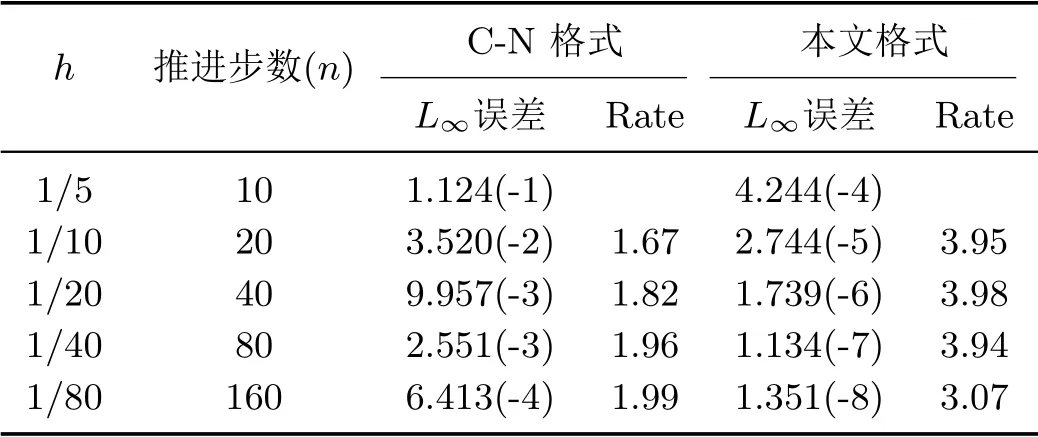
表5 问题3 当λ=τ/h=0.5,a=0.5,t=1 时刻的最大绝对误差及收敛阶

问题3为非齐次问题,由于文[7]的方程模型为齐次方程,不能计算非齐次问题,因此该问题我们采用本文格式和C-N进行计算和比较,表5给出了两种格式在不同空间步长h下,当t=1时的最大绝对误差和收敛阶.可以看出当λ=τ/h=0.5,a=0.5 时,C-N格式在时间和空间上都为二阶精度,而本文格式时间和空间均为四阶精度.

5.结论

本文针对一维对流方程提出了一种两层隐式高精度紧致差分格式,时间和空间均采用泰勒级数展开法以及截断误差余项修正法进行处理,格式截断误差为O(τ4+τ2h2+h4),即该格式在时间和空间上均可达到四阶精度.并通过von Neumann方法分析得到该格式为无条件稳定的.最后通过三个数值算例验证了格式的精确性和稳定性.通过上述研究,我们可以得出如下结论:

1.文献(如[10-11])中的高精度格式往往是时间多层格式,需要另外构造启动步的计算格式,如果采用低精度格式启动,必然会影响以后时间层的计算精度.而本文格式仅为两层格式,无须启动步的计算,时间即可达到四阶精度.

2.文献(如[1,10-11])中的高精度格式空间方向上往往超过三个网格节点,导致靠近边界的内点计算困难,需要采用特殊处理,而本文格式仅用到三个网格节点,可以有效避免这一问题.

3.尽管本文格式要求2,这是本文格式的一个缺陷,但是由于本文格式是无条件稳定的,从理论上讲可以采用任意网格比,因此可以很容易避开2的条件限制,使得这一缺陷并不太影响格式的使用.

5.本文方法可直接推广到二维和三维问题中去,我们将另文报道.