中考中的一元一次不等式问题
2019-06-27肖学军
◎肖学军

一元一次不等式是初中数学的基础性内容,时常成为中考命题中必不可少的测试内容。本文拟以2018年部分省市的中考题为例,按考点归类加以剖析。
考点一:不等式的性质
例1(2018·宿迁)若a<b,则下列结论不一定成立的是( )。
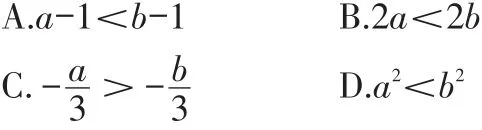
【解析】由不等式性质容易知道,选项A、B、C中的不等式是成立的。选项D有时成立,如当a、b均为正数时成立;有时又不成立,如当a=-2,b=1时。故答案选D。
【点评】本题主要考查不等式的性质,我们只要掌握了不等式的性质便容易作出正确判断。本题要寻找的是不一定成立的结论,不是错误结论,这是审题时必须要引起重视的。
考点二:求不等式(组)的解集及其数轴表示
例2(2018·威海)解不等式组并将解集在数轴上表示出来。
【解析】解不等式①,得x>-4;解不等式②,得x≤2。根据“大小小大中间找”,可得原不等式组的解集为-4<x≤2,在数轴上表示如下图所示:

【拓展】(2018·贵港)若关于x的不等式组无解,则a的取值范围是( )。
A.a≤-3 B.a<-3 C.a>3 D.a≥3
解决本题的关键是要利用不等式组取解集的方法,将问题转化为不等式:a-4≥3a+2,答案为A。
【点评】这类问题是不等式问题的常见题型。要能够熟练应用求不等式组解集的法则,即“同大取大,同小取小;大小小大中间找,大大小小无解了”。
考点三:不等式(组)的整数解问题
例 3(2018·包头)不 等 式组的非负整数解有________个。
【解析】首先解不等式组,得到不等式组的解集为x<4,从而该不等式组的非负整数解为0、1、2、3这4个,故答案为4。
【拓展】(2018·荆门)已知关于x的不等式3xm+1>0的最小整数解为2,则实数m的取值范围是( )。
A.4≤m<7 B.4<m<7
【点评】这两题均为不等式的整数解问题,例3比较直接,通过解集得出答案;拓展题关键是要由最小整数解得出符合题意的不等式。
考点四:不等式(组)的应用问题
例4(2018·南京)如图,在数轴上,点A、B分别表示数1、-2x+3。
(1)求x的取值范围;
(2)数轴上表示数-x+2的点应落在___。
A.点A的左边 B.线段AB上
C.点B的右边

【解析】(1)根据数轴上的点表示的数右边的总比左边的大,可得不等式-2x+3>1,解得答案x<1;
(2)由x<1,得-x>-1,于是有-x+2>-1+2,根据不等式的性质,可得点在A点的右边;根据作差法:-2x+3-(-x+2)=1-x>0,可得点在B点的左边。故选择B。
【拓展】思考1.若将(2)中的点记为C点,这三点中存在某点是另外两点所构成线段的中点吗?
由(2)解答知C点在线段AB上,故只有C点有可能为线段AB的中点。计算AC和BC长度可知,结论成立。
思考2.若点B右侧有一点D所表示的数是2x+5,且2<BD≤6,试求x的取值范围。
事实上,BD=(2x+5)-(-2x+3)=4x+2。根据题意可得不等式组解得0<x≤1。又由问题(1)知x<1,所以x的取值范围为0<x<1。
【点评】本题主要考查同学们灵活应用不等式的有关知识解决问题的能力,既考查了应用数轴比较两个实数大小和不等式的性质应用,又着重考查了数形结合的思想。
例5(2018·济宁)“绿水青山就是金山银山”,为保护生态环境,A、B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:________________________________

10__________________________________16 68000_________村庄清理养鱼网箱人数/人_____清理捕鱼网箱人数/人_____总支出/元________A______B__15 9__________57000
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
【解析】(1)设清理养鱼网箱的人均费用为x元,清理捕鱼网箱的人均费用为y元,
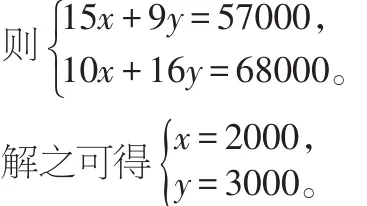
(2)设m人清理养鱼网箱,则(40-m)人清理捕鱼网箱,根据题意,列不等式组

解得:18≤m<20,
∵m为整数,∴m=18或m=19。
则分配清理人员方案有两种,
方案一:18人清理养鱼网箱,22人清理捕鱼网箱;
方案二:19人清理养鱼网箱,21人清理捕鱼网箱。
【拓展】思考1.这些方案中,哪种方案总支出较少?
对此,可以分别求出两个方案的总支出,通过比较可知方案二总支出较少。
思考2.若将总支出改为不超过110000元,问有几种分配方案?其中哪种方案总支出最少?
仿照本题解法可得10≤m<20,用列表法知共有10种方案。若分别求出10种方案的总支出,则很繁杂。由于总支出代数式为2000m+3000(40-m),化简即为120000-1000m,易知m越大,总支出越少。10种方案中,还是m=19时的方案总支出最少。
【点评】本题主要考查同学们运用二元一次方程组和不等式组的有关知识来解决实际问题的能力。题目中的有关信息由表格给出,问题(1)较为容易,所涉及的两个未知量通过列出二元一次方程组即可求解;问题(2)中有两个不等关系,这是列出不等式组的重要依据。
