数轴是一把“金钥匙”——利用数轴解一元一次不等式组的相关问题

◎刘玉兵

同学们在上学期已学过数轴，都知道利用数轴可以直观地表示数，可以帮助我们理解绝对值与相反数的含义，也可以比较数的大小等。那么在解一元一次不等式组的时候，数轴有什么作用呢？它能把数与形结合在一起，将抽象转化为直观，快速且准确地找出解集，特别是在解一些含有字母参数的不等式组的有关问题时，优越性更大。

例1苏科版《数学》七年级下册第135页例1：

解：在数轴上表示不等式x≤-1和x＜2的解集（如图1）：

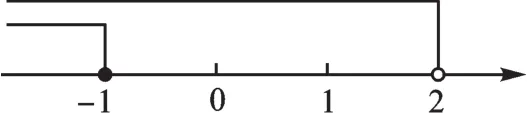
图1

由图1可知，不等式组的解集是x≤-1。

【点评】解一元一次不等式组分三步：求解、画图、定解集。第一步，分别求出不等式组中每个不等式的解集，即求解；第二步，画数轴，分别表示出每一个不等式的解集，即画图；最后在数轴上找出各个不等式解集的公共部分，即定解集。书中第136页例2、例3也是如此。

例2 解不等式组

【分析】如果一个不等式组含有两个以上的不等式，我们同样可以先求出各个不等式的解集，并利用数轴确定各个解集的公共部分。若有公共部分，则此公共部分即为不等式组的解集；若无公共部分，则不等式组无解。

解：解不等式①，得x＞-2，

解不等式②，得x＜4，

解不等式③，得x＞6。

在数轴上把各个不等式的解集表示出来（如图2）。

图2

所以这个不等式组无解。

【点评】在数轴上画出各个不等式的解集，同学们就非常容易观察出这三个解集没有公共部分，从而确定这个不等式组无解。

例3（2017·宿迁）已知4＜m＜5，则关于x的不等式组的整数解共有（ ）个。

A.1 B.2 C.3 D.4

【分析】本题表示出两个不等式的解集不难，难在题中的m不是一个准确的值而是一个范围，但是我们如果在数轴上表示出它们的解集之后，就会很容易发现此不等式组的整数解的个数。

解：解不等式①，得x＜m，

解不等式②，得x＞2。

∵4＜m＜5，

在数轴上把各个不等式的解集表示出来（如图3）。

图3

∴原不等式组可取的整数解为3、4两个。故选B。

例4苏科版《数学》七年级下册第141页第14题：

（1）如果这个不等式组无解，求a的取值范围；

（2）如果这个不等式组有解，求a的取值范围。

【分析】结合数轴，若不等式组无解，说明属于x＜a与x＞1的解集没有公共部分，那表示a的点应在1的左边和1这一点，因此a的取值范围为a≤1；若不等式组有解，则与（1）的情形相反，a应取除a≤1以外的数，即a＞1。这两问在解题过程中需要注意字母的取值范围是否包括端点。

解：把x＞1的解集在数轴上表示（如图4）。

图4

（1）若不等式组无解，则a≤1；

（2）若不等式组有解，则a＞1。

例5（2018·泰安）不等式组有3个整数解，则a的取值范围是（ ）。

A.-6≤a＜-5 B.-6＜a≤-5

C.-6＜a＜-5 D.-6≤a≤-5

解：由x＜-1，

解得：x＞4，

由4（x-1）≤2（x-a），

解得：x≤2-a，

故不等式组的解为：4＜x≤2-a，

由原不等式组有3个整数解，故这3个整数解只能是5、6、7。

由数轴可确定2-a的范围（如图5）。

图5

解得：7≤2-a＜8，

进而解得：-6＜a≤-5。

故选：B。

【点评】本题的难点之一是不等式组中有字母参数，但这不难解决；难点之二是把2-a看成一个整体，然后根据原不等式组解的情况在数轴上确定2-a的范围，首先应在7与8之间，其次判断是否包括端点7和8，这时数轴的优势就不言而喻了。

以上五例由浅入深、由易到难，我们发现数轴在解一元一次不等式组中的作用既简捷直观又快速准确。希望同学们抓住这把“金钥匙”，在数学学习中注意数形结合思想的运用，更好地享受数学带给大家的快乐。