集装箱地下物流系统节点选址
2019-06-27周志远
涂 敏,周志远
(武汉理工大学 交通学院,湖北 武汉 430063)
1 引言
多年来我国外贸量持续增长,港口集装箱吞吐量在全球领先,其中上海港更是连续多年占据世界集装箱吞吐量榜单的首位。但大部分港口的集疏运体系高度依赖公路运输,上海港同样如此,据测算,2012年上海港约有56.8%的集装箱通过公路集疏运。过高的公路集疏运比例,加上城市自身的物流活动,给城市带来了诸多问题,包括:城市拥堵状况的逐年恶化、物流设施侵占城市用地、物流车辆过度耗费能源、生态环境被破坏等。逐渐恶化的城市交通又会影响港口集疏运系统的高效运行,进而影响港口的集装箱吞吐效率,甚至降低港口的竞争力。良好的城市交通系统是实现港城间稳定协调发展的基础,而将港口集装箱集疏运过程转移至地下进行运输,能够改善城市整体环境、缓解城市交通拥堵问题、缓和港城间发展矛盾。
良好的城市交通系统是城市经济活动的基础,对提高城市经济水平和改善人民生活质量都起着不可替代的作用。由于港口集疏运模式不合理,公路运输比例过高带来交通拥堵、环境污染等一系列问题,对城市的发展造成了不利影响。为了改善拥堵的城市交通,减少环境污染,绝大多数城市采取增加道路供给的措施,例如新修、拓宽改建城市道路,同时对市内货流采取一定限制措施。这些举措虽然在一定程度上缓解了城市内部交通状况,但却对城市内的贸易流通、工业生产造成了一定影响。
目前已有不少学者积极推进地下物流理论的研究。Joseph V.Sinfield,Herbert H.Einstein[1]在实际环境中验证了地下管道运输系统的可行性;Dietrich Stein[2-3]设计了以Cargo Cap 为运载工具的地下物流系统概念模型,提出托盘可作为地下物流系统的集装单位,设计了地下物流系统的悬挂轨道舱体概念模型和重力轨道舱体概念模型。项汉桢[4]以南京市仙林区地下货物运输节点选址及线路规划为对象,建立了以最低物流成本为目标的多目标优化模型;黄欧龙[5]初步探讨了地下物流系统网络规划与设计;包敏[6]在确定物流节点候选集的基础上,建立了基于集合覆盖度的物流节点选址模型,并设计了基于Flody 算法和主目标法的求解算法;李珍萍[7]以节点间的连接方式为决策变量建立了ULS网络规划的混合整数规划模型;刘桂汝等[8]采用二分K-均值算法和免疫算法相结合的方式对物流节点选址进行求解,结果表明该算法可用于求解组合优化问题。胡万杰等[9]分别从ULS一级节点的选址、二级节点的优化以及网络路径选择、网络效能评估等方面对地下物流系统一系列问题进行了建模与分析;王曼[10]、谢丽[11]、闫文涛[12]等分别建立了基于双层规划模型的ULS 节点选址模型。
在本文试图建立的地下物流节点选址双层规划中,上层规划基于政府规划者的角度,将物流节点的选址与建设成本、运输费用等要素联系起来,使物流节点的构建成本最低;下层规划则是基于每个用户最优原则,是对客户的物流节点选择行为的模拟,并以使每个客户花费的费用最低为目标函数。下层规划的求解能够得到客户需求量在各个物流节点中的分配情况,进而为上层模型的求解提供数据支持。
2 集装箱地下物流节点选址模型建立
地下物流网络节点是地下地上物流系统衔接的窗口,除此之外还具有管理功能、信息处理功能,肩负着整个地下物流系统的货物运输、装卸搬运、流通加工、储存保管以及信息传递功能。
2.1 模型建立的假设
基于集装箱地下物流网络的特点,为简化模型,对模型作出以下假设:
(1)运输2个20尺集装箱和1个40尺集装箱,单位距离运输费用相同;
(2)各个地下网络节点的建设费用已知;
(3)规划初期,暂不考虑地质条件的影响;
(4)货源地、地下网络节点、港区为多对多关系,且一个货源地至少被一个地下网络节点覆盖,一个地下网络节点至少有一个货源地供货;
(5)由于没有现存的地下物流节点,因此规划时不考虑其他原始节点的影响。
2.2 双层规划模型的建立
双层规划问题为一种具有双层递阶的系统优化问题,包含一个上层问题和若干个下层子问题。针对本文的地下物流节点选址问题,该问题中包含最优目标不同的两个参与者,即系统规划者和系统使用者。而这两个参与者的最优目标又相互制约,并且通常情况下以系统规划者的最优目标为主,故采用双层规划模型来描述这种关系是比较合适的。
(1)上层模型的建立

式中:
M—港区数量,i=1,2,...,m;
Q—拟建备选集装箱地下物流节点数量,k=1,2,...,q;
N—箱源地数量,j=1,2,...,n;
bj—箱源地提供的集装箱量;
Cik—港区至备选地下物流节点的单位运输费用;
Dkj—箱源地至备选地下物流节点的单位运输费用;
Xik—港区到备选地下物流节点的运输量;
Xkj—箱源地到备选地下物流节点的运输量;

Fk—备选地下物流节点k的建设费用;
H—地下物流节点总投资限额;
Wk—地下物流节点集装箱处理能力。
模型中,式(1)为上层目标函数,其目标为港区至地下物流节点运输费用、备选地下物流节点至箱源地的运输费用以及地下物流节点的建设费之和为最低。其余各式分别是对模型各中参数的约束、限定,式(2)约束地下物流节点的建设费用之和不大于总投资费用;式(3)表示地下物流节点服务能力大于各目的点运量和;式(4)表示从港区运往地下物流节点的运量不能大于该节点服务能力;式(5)表示所有运至地下物流节点的货物均会被运出。
(2)下层模型的建立
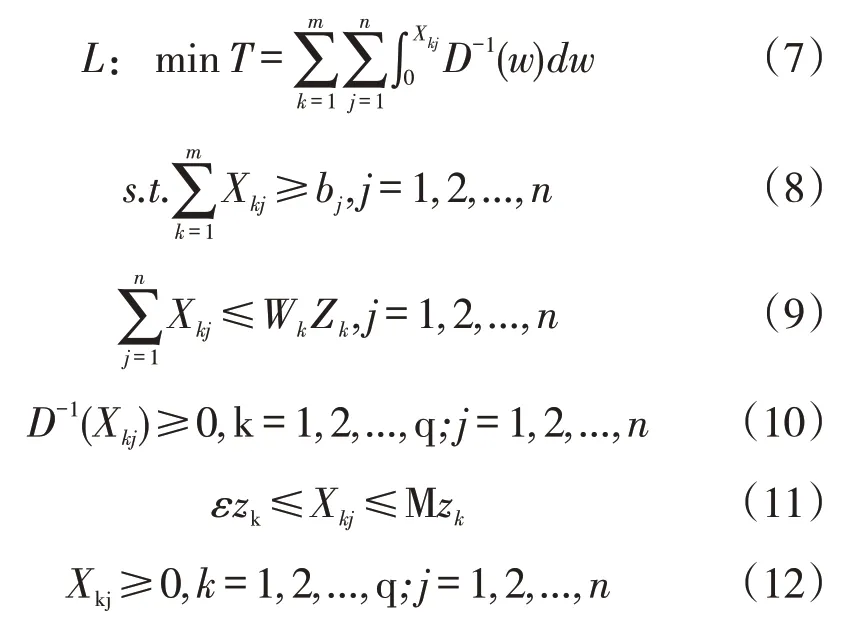
符号含义同上层模型,其中式(7)为下层目标函数,D-1为效用函数,表示箱源地在选择地下物流节点时其需求被满足程度;式(8)表示地下物流节点服务能力大于各目的点运量和;式(9)表示从港区运往地下物流节点的运量不能大于该节点服务能力;式(10)表示箱源地运送至各物流节点的物流量不为负值;式(11)中,ε为一任意小数,此处取ε=0.1。在本模型中,选用D-1(xkj)=β ln xkj-vizi,其中β为修正系数,在此处取β=1。
3 双层规划模型的求解
对本文所建立的模型来说,求解的关键在于确定反应函数的具体形式。通过对所建立下层模型的分析可得,下层目标函数表明在平衡状态下,客户在各物流节点所分配的需求量与配送中心选址方案之间的关系。即在下层模型中,判断函数Zi为已知,当Zi=0,此时Xkj=0,故可去掉约束式(7);当Zi=1,则式(11)可直接写为Xkj≤M,其中M为任意大的数,此约束式必定满足,可不予考虑。
为求得上文提到的反应函数的具体形式,将约束式(11)整理为式(12)(模型中式子不变化)。

式中:ykj为松弛变量,当zk=0时,可直接得出Xkj和ykj的值;当zk=1时,可通过已有方法求解下层模型式(7),继而求出平衡状态下各物流节点所分得的箱源地的箱量,再利用式(12)计算松弛变量ykj*的值。此时,反应函数的形式见式(13)。

将求得的反应公式带入上层模型目标函数式(1)中,能够求得上层模型的最优解,继而将所得解带入下层模型就可得到箱源地箱量在各物流节点的分配,重复上述过程,直到最终得到能收敛于双层规划模型的最优解。
上述求解过程本质上是一个基于式(12)的启发式算法,具体步骤如下:
第一步:选取初始解,取迭代次数a=0;
第二步:基于已给定的,对下层模型进行求解,得到;
第三步:在式(13)中计算,并将式带入上层规划模型目标函数中,对上层模型进行求解并得到一组新的
目前关于双层规划问题的求解,学术界给出了诸多方法,如KKT条件法(Karush-Kuhn-Tucker method,亦可简称为K-T法)、直接搜索法(Direct Search Method)及下降法(Descent Method)、启发式算法等。针对本文所建立的双层规划问题,因计算过程较为复杂,可行解较多,精确性算法求解较为困难,使用启发式算法求解比较合适。其中,遗传算法具有全局收敛快、鲁棒性强等特点,故选取遗传算法作为本文模型的求解算法。
根据上文所描述双层规划问题的求解方法,及遗传算法通用求解步骤,可得到针对本问题的遗传算法求解步骤,具体如下:
第一步:编码及初始化。枚举出下层规划中所有可行解xk。在每个xk下,对上层规划中的0-1变量zk进行遗传编码,采用离散数组编码的形式,见表1,使用Matlab遗传算法工具箱crtbp函数完成。

表1 编码数组
第二步:适应度值计算。采用线性加权法设计模型的适应度函数。首先对量纲进行归一化,同时规范化F(x,y)以及f(x,y)。将x=xk时的F(x,y)、f(x,y)的最大值及最小值分别记作Fkmax、Fkmin、fkmax和fkmin,利用式(14)和式(15)对F(x,y)和f(x,y)进行规范化处理。然后分别给目标函数赋予权重系数ω1和ω2,ω1、ω2大于零且ω1+ω2=1。最后可得到适应度函数为Fitn=ω1φ1(y)+ω2φ2(y)。

第三步:选择。选择算子采用随机遍历抽样。用Matlab软件中GA工具箱sus函数完成。首先计算个体适应度值,fitn(yk)(k=1,2,...,m;m为种群大小);其次计算个体被遗传至下一代的概率;然后计算个体累计概率;最后选择个体数量,个体数量由种群初始化时设置的代沟决定,选择方式为等距离选择,第一个指针位置由[0,1/n]的均匀随机数决定。如图1所示。

图1 随机遍历选择
第四步:重组。重组算子的设计采用单点交叉。单点交叉用Matlab软件中GA工具箱xovsp函数完成。
第五步:变异。变异算子采用实值变异。该变异采用Matlab软件中GA工具箱mutbga函数完成,变异概率设定为P,变异范围设定为[1,n]的整数,然后返回变异后的种群。最后采用GA工具箱reins函数,对种群重新插入,回复种群中个体的数量。
4 上海市集装箱地下物流网络节点选址研究
4.1 上海市地下物流节点的确定
根据上海国际港务(集团)有限公司业务处的信息,上海集装箱集疏运的90%都集中在江浙沪三省市。
(1)江苏、浙江方向箱源进出上海界面的确定。江苏、浙江地区集装箱首先通过市外高速、国道网络运输,到达上海市域范围后再接入A20、A30公路抵达目的港区。其中A12、A11、S26、A5仅服务于江苏方向集装箱货源,A4、A8、G320仅服务于浙江方向集装箱,A9及G318服务于两省的集装箱货源。共14个关键节点,该部分节点可认为是上海港集装箱地下物流网络的市外箱源地。即对上海港而言,这两省的集装箱公路集运,由集卡车通过市外高速、国道路网运输至上海市区边缘与A20、A30高速交汇处,通过位于该处附近的地下集疏运地面设施转运至地下,通过地下运输网络运输至目的港区,上述所描述过程为上海港集装箱的集运过程,疏运过程则与之相反。通过将本应通过地面运输的集装箱转移至地下,从而缓解集疏运给上海市内交通带来的诸多负面影响。
(2)上海市市内箱源地的确定。上海市市内箱源地主要为分布于上海各区的出口加工区和工业区内,其中园区内箱源较多且占上海市进出口总额比例超过1%的园区主要有:金桥出口加工区、松江出口加工区、嘉定出口加工区、闵行出口加工区、青浦出口加工区、漕河泾出口加工区以及外高桥保税区。其中位于浦东新区内的金桥出口加工区和外高桥保税区进出口总额占上海市进出口总额的60%以上,是上海市市内最主要的集装箱箱源地。本文选取这7个主要园区为上海市市内箱源地。
(3)地下物流节点的确定。目前集装箱地下物流的应用较少,本文参考比利时安特卫普港集装箱地下物流节点进行分析。根据该港集装箱地下物流系统建设公司DENYS NV的相关数据,采用垂直竖向进出口形式的地下物流节点,年运输能力可达180万自然箱。考虑到港口机械能力的提升,如我国洋山四期码头的全自动吊具,可一次搬运一个40尺集装箱或两个20尺集装箱,即可认为在吊具搬运集装箱速度不发生变化的情况下,单个集装箱地下物流节点的年操作能力为360万TEU。
由于上文所确定的箱源地均分布在上海市区外围,同时采用垂直竖向进出口形式的地下物流节点的地面部分占地较少,故在选址过程中不考虑用地环境因素。因此本文中地下物流节点的布置应尽量靠近箱源地。
根据《上海市城市总体规划(2017-2035年)》,截止2035年,上海港集装箱吞吐量将维持在4 000 万-4 500万TEU水平,同时水路集装箱集疏运比例将上升至接近50%。因此若在21个箱源地均设置集装箱地下物流节点,那么该系统运输能力将大幅超过所需值,造成极大浪费。
因此本文将基于所建立双层规划模型,对上海市集装箱地下物流系统的选址进行优化。
4.2 上海市地下物流系统节点选址实证研究
通过前文分析,此模型可归纳为21个箱源地的集装箱(j=21)在21个物流节点(k=21)中进行选择,最后通往两个港区(i=2)的问题,在此处取ji=ki,即物流节点的选址靠近箱源地。三者之间关系如图2所示,箱源地、物流节点及港区之间空间关系如图3所示,各点坐标见表2。其中,洋山港区远离上海市,由全长超过30km的东海大桥唯一承担公路集装箱集疏运量,并且在规划中,已有东海二桥的建设计划,同时按照工程经验,相同标准的跨海大桥与海底隧道,海底隧道建造成本远大于跨海大桥。故在本文中,将洋山港区集装箱地下集疏运系统节点设置于芦潮港区内。货源地至地下物流节点、地下物流节点至港区之间集装箱运输费用只与距离相关,且认为2个20尺集装箱运输费用与1个40尺集装箱运输费用相同,已知我国铁路运输成本约为0.064元/t·km,公路运输成本为0.297元/t·km,集装箱重取平均值30t,因此地下部分运输费用取2.0元/TEU·km,地上部分取8.91元/TEU·km,由于暂无相关数据支撑,并且考虑到地下设施的高建设成本,故单个地下物流节点建设成本取一亿元整。上海市本地货源地集装箱量取前文双层规划模型求得的预测值,外地货源地集装箱量将江苏、浙江集装箱生成量预测值均分至各相邻界面。具体相关数据见表3、表4。
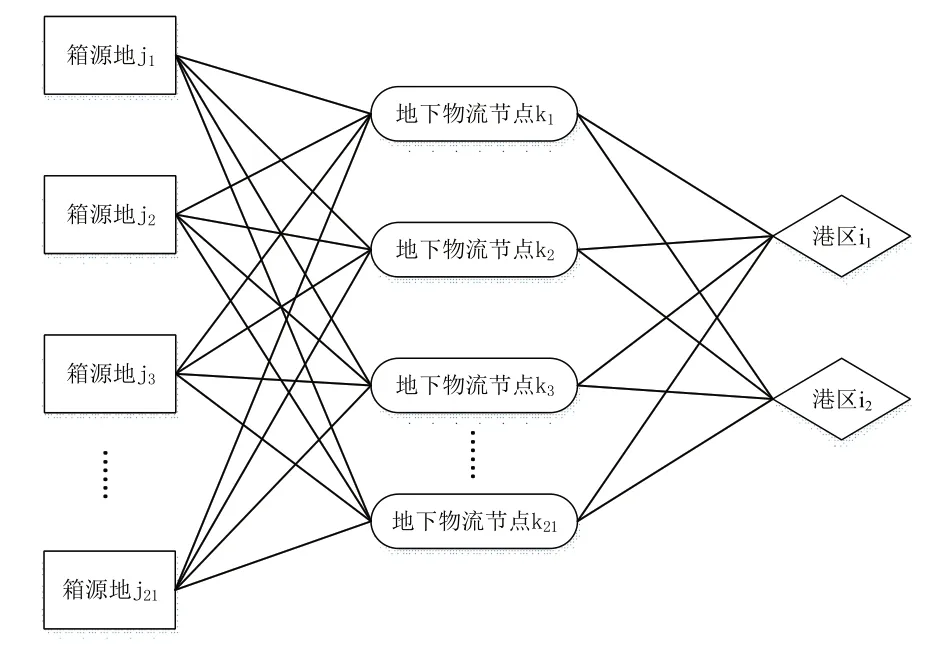
图2 集装箱地下物流线路图
4.3 下层模型求解
首先将前文所建立下层模型中目标函数进行整理,可得式(16)。
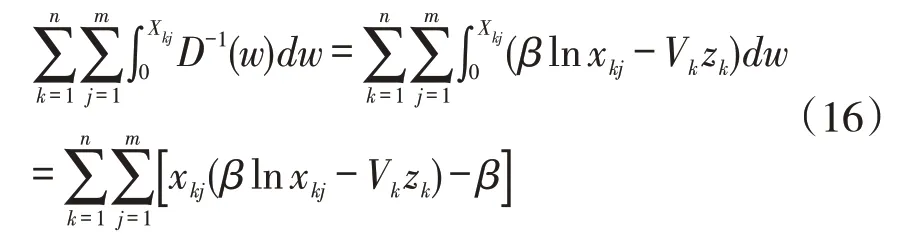
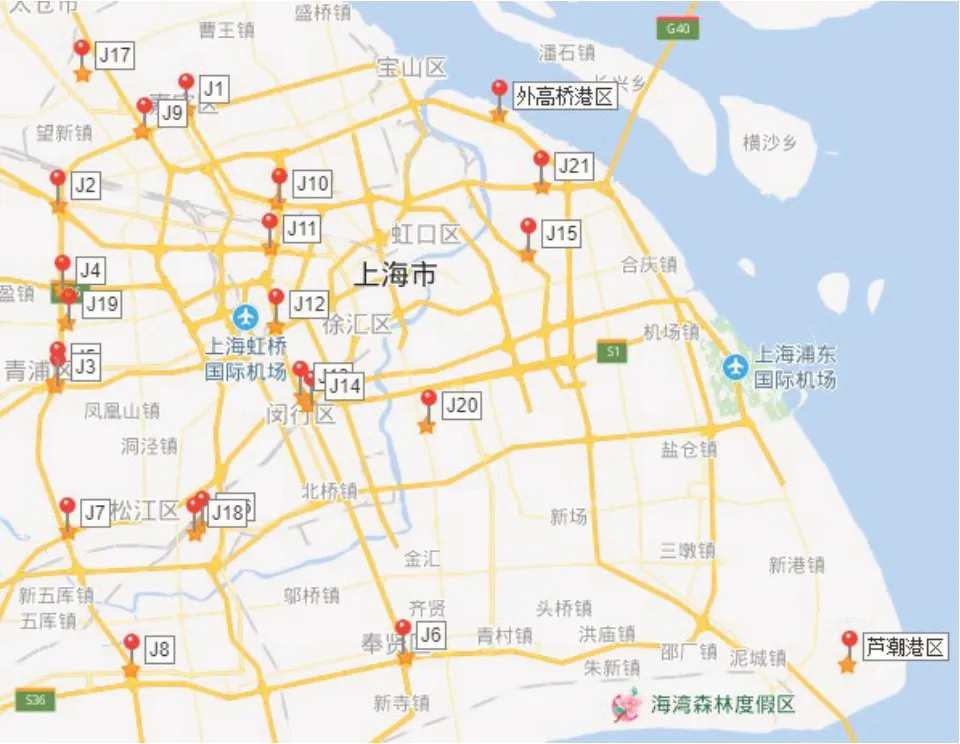
图3 上海市集装箱地下物流系统节点图

表2 上海市集装箱地下物流系统节点坐标
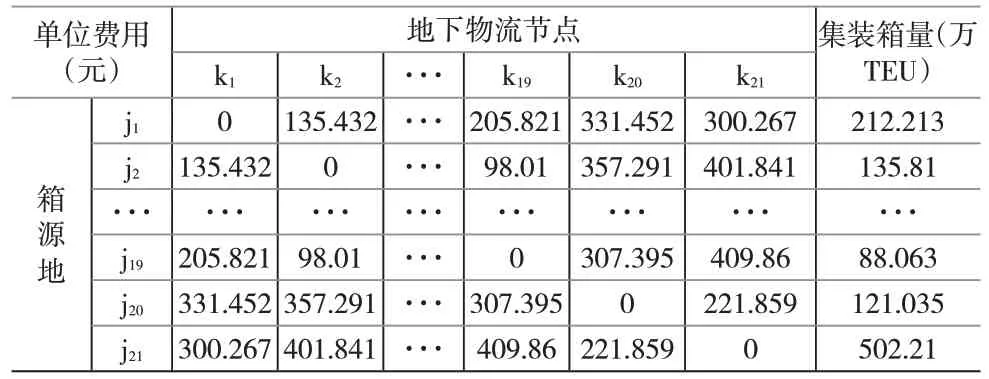
表3 箱源地至地下物流节点的单位运输费用及集装箱量
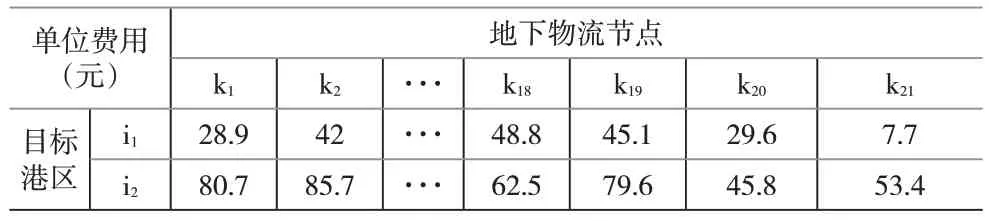
表4 地下物流节点至目标港区的单位运输费用
在下层模型中,已有待选物流节点,则求使下层模型目标函数达到最小的xkj是一个非线性规划问题。求解该问题可使用Matlab软件中的fmincon工具箱。具体方法见式(17)。
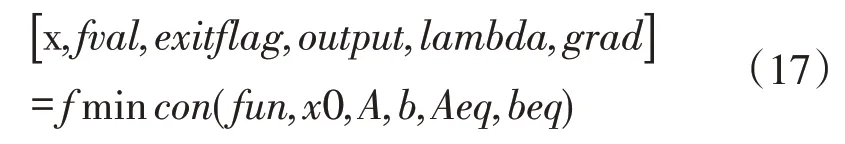
式中,x 为待求最优解,fval代表目标函数值,exitflag表示该函数的有效性,与无约束调用有相同意义,output为包括优化信息的输出参数。
所求得箱源地对物流节点的选择方案见表5。

表5 箱源地对物流节点之间的选择方案
4.4 上层模型求解
上层规划模型使用遗传算法进行求解,本文中采用Matlab 软件中谢菲尔德大学遗传算法工具箱进行求解。具体参数设置如下,初始种群大小:200;迭代次数:100;变异率:0.05;交叉率:0.6,染色体长度35,代沟0.9。选取方案1-10中有代表性方案的遗传算法性能跟踪图如图4—图8所示。方案1-10 的平均适应度值见表6。

图4 方案3遗传算法性能跟踪图
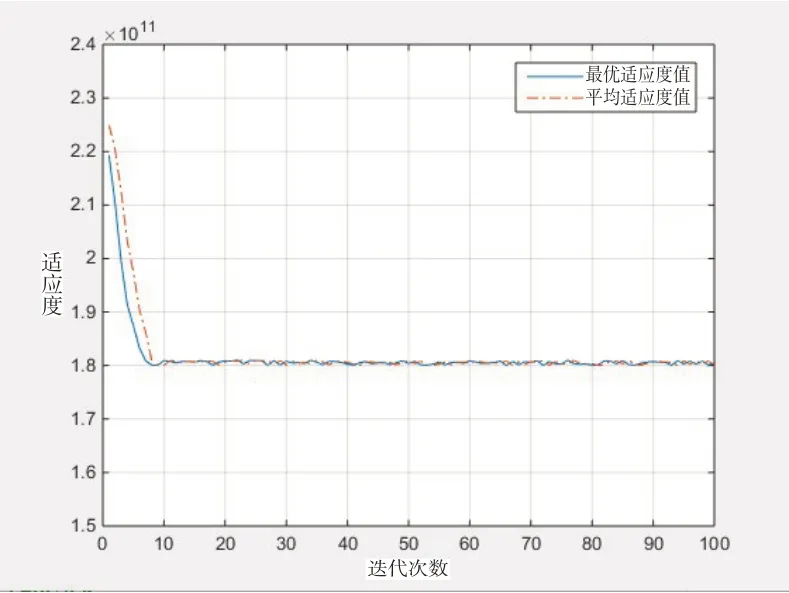
图5 方案8遗传算法性能跟踪图
图6 方案9遗传算法性能跟踪图

图7 方案4遗传算法性能跟踪图
图8 方案5遗传算法性能跟踪图
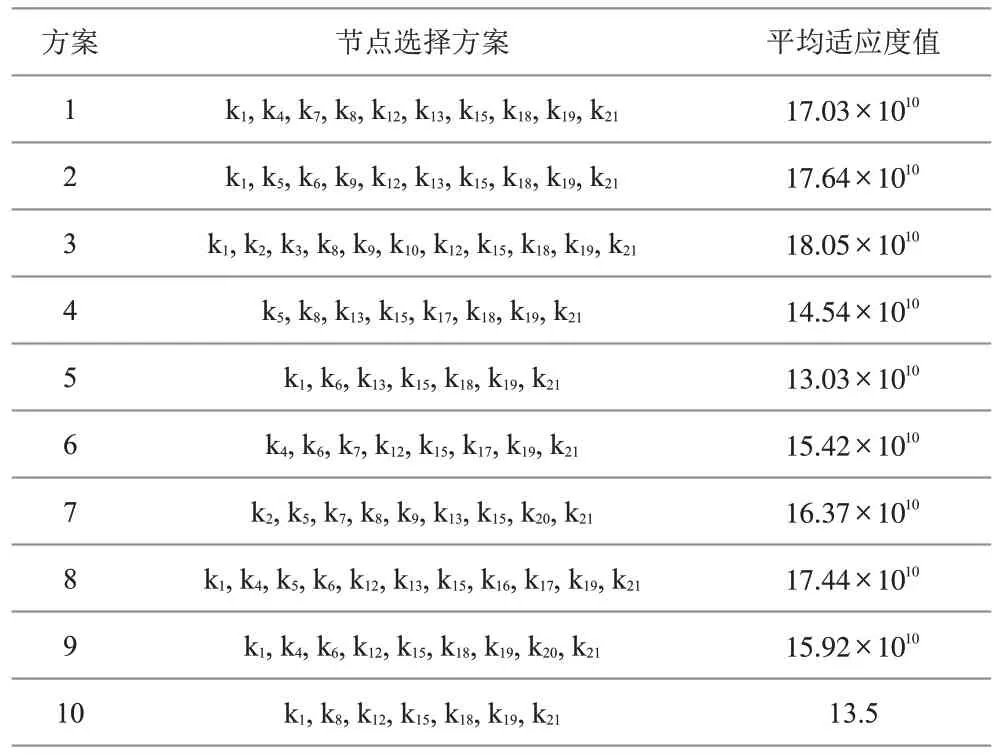
表6 双层规划求解结果
从表6可以看出,当有7个备选物流节点被选择时,即为方案5 时,所选取物流节点分别为k1、k6、k13、k15、k18、k19、k21,系统有最低的成本,即为表6平均适应度值13.03×1010元。其中物流节点k1所服务的箱源地为J1、J9、J17,且这三个箱源地的集装箱生成量,全部经由物流节点k1运输至目标港区;物流节点k6所服务的箱源地为J6、J8,这两个箱源地的集装箱生成量,全部经由物流节点k6运输至目标港区;物流节点k13所服务的箱源地为J10、J11、J12、J13、J14、J20,这六个箱源地的集装箱生成量,全部经由物流节点k13运输至目标港区;物流节点k15所服务的箱源地为J15、J21,这两个箱源地中,箱源地J15的全部集装箱生成量经由物流节点k15运输至目标港区,箱源地J21的集装箱生成量中,物流节点k21所不能满足的生成量,经由物流节点k15运输至目标港区,在预测年,该运输量为142.21 万TEU;物流节点k18所服务的箱源地为J7、J16、J18,这三个箱源地的集装箱生成量,全部经由物流节点k18运输至目标港区;物流节点k19所服务的箱源地为J2、J3、J4、J5、J19,这五个箱源地的集装箱生成量,全部经由物流节点k13运输至目标港区;物流节点k21所服务的箱源地仅为J21,箱源地J21的集装箱生成量,在物流节点k21服务能力范围内,全部满足经由物流节点k21运输至目标港区。方案5 备选物流节点空间示意图如图9所示。

图9 上海市集装箱地下集疏运系统节点选址图
5 结语
(1)本文构建了基于成本最优和用户选择的地下物流节点选址模型并进行了案例分析。上下两层模型分别考虑规划建设者利益和客户利益。其中下层模型为用户选择模型,基于每个用户的最优原则,是对客户的物流节点选择行为的模拟;上层模型是将物流节点的选址与建设成本、运输费用等要素联系起来,使物流节点的构建成本最低。
(2)所选案例为上海市集装箱集疏运系统,以上海市为例,分析集装箱集疏运系统的主要流向及流量,采用可拓聚类预测模型,对主要箱源区集装箱生成量进行了分析预测;基于双层规划模型,结合遗传算法,在备选方案中选择了适应度最小的节点选址方案,确定了7 个上海市集装箱地下物流网络节点,研究结果可为上海市集装箱地下物流网络选址提供理论参考。
(3)地下物流系统的规划建设应是一个复杂的系统工程,该系统的规划建设涉及到城市功能布局的未来规划、物流、信息技术、自动化技术、土木工程建设水平、新型载运工具等学科的综合知识。本文针对上海港集装箱地下集疏运系统的研究,只考虑了集疏运相关因素,考虑还不够全面,在未来研究乃至实际规划建设中,应综合考虑多方因素。
