黑土区坡耕地壤中流水平迁移动力学模型研究

曹程鹏, 张 飞, 段建明

(1.绥化学院 农业与水利工程学院, 黑龙江 绥化 152061; 2.东北农业大学 水利与土木工程学院, 哈尔滨 150030)

我国东北黑土区犁底层普遍存在，导致降雨过程中土壤内部壤中流的产生，壤中流作为径流不可或缺的重要组成部分，对农业生产及生态环境治理有着重要意义。基于不同的假设，国内外学者提出了许多壤中流产生的机理模型，但每种模型都有其应用局限性，不能将已有模型直接应用于实际田间生产活动。Richard模型作为经典非饱和土壤水分运动模拟模型在壤中流的模拟中有所应用[1-3]，但其不能直接求出渗流区的侧向出流量。贮水泄流模型从宏观的水量平衡角度出发，虽然可以直接获得坡面出口断面处侧向出流量[4-5],但其应用局限性较大。动力波模型假设不透水层或准不透水层边界上饱和区域内流线平行于底板，且水力梯度等于基岩坡度[6-7]，该模型早期应用较多。近年来，“双超”模型及其改进模型逐渐应用于土壤壤中流过程的模拟中，由于其模拟参数变动较大，实际模拟效果并不十分理想[8-9]。

黑土区坡耕地犁底层对土壤水分入渗虽然存在阻滞作用，但犁底层中的垂向入渗仍然是土壤内部水分迁移的主要形式，这就造成了前人提出的贮水泄流模型及动力波等模型应用受到限制，能够同时反映犁底层中土壤水分垂直迁移与犁底层上部壤中流水平迁移相互作用的模型更具合理性。为此，本文基于能够连续模拟犁底层上部土壤及犁底层内部土壤水分垂直迁移的Richard模型，借鉴动力波模型及“双超”模型原理，提出适合黑土区坡耕地壤中流水平迁移的机理模拟模型，并利用人工模拟降雨试验对模型进行验证，以期为黑土区坡耕地农田土壤水肥管理提供科学依据。

1 试验材料与方法

1.1 模型原理

土壤水分入渗采用一维垂直土壤水分运动的Richard方程计算[10]：

(1)

式中：t表示时间(min)；θ表示含水量(%)；D(θ)表示土壤水分扩散率(cm2/min)；k(θ)表示非饱和导水率(cm/min)；θ(z,t)表示在深度为z处的土壤含水量(%)。方程(1)的初始和边界条件为：

(2)

式中：R为入渗(cm/min)；θi为土壤初始含水量(%)；tp表示产流时间(min)；i表示入渗率(cm/min)。

根据试验条件，得到方程(1)的上边界条件Parlange模型[11-12]：

(3)

采用Brooks-Corey[13]的水分特征曲线模型：

k(Θ)=ksΘM

(4)

(5)

(6)

式中：K(Θ)为非饱和导水率；D(Θ)为土壤水分扩散率；Θ为有效饱和度；N,M为形状系数；M=3N+2；hd为土壤进气吸力；l为弯曲度；θ0(t)为土壤表层含水量；Ks为土壤饱和导水率(cm/min);θs为土壤饱和含水量;θr为土壤滞留含水量。通过数值方法求解方程(3)得到土壤饱和前的上边界条件，通过垂直和水平土柱(扰动土)入渗试验得到土壤参数见表1。

由于土壤容重在犁底层处发生显著变化，犁底层以上土壤与犁底层内部土壤进行土壤水分垂直迁移模拟时需要采用与土壤特性相对应的参数。2组参数需要分别测量获得(表1)，结合公式(1)将犁底层及其以上土壤作为一个整体，不同位置采用不同参数，利用数值法连续模拟湿润峰下移过程。计算犁底层上边界入渗通量时，采用公式(2)中入渗率i作为犁底层上边界入渗通量计算公式，得到犁底层上边界入渗能力。假设犁底层以上入渗水未触及犁底层时段，土壤饱和层与集水槽挡板相接触的饱和土壤中土壤水分无水平运移，结合动力波模型中假设犁底层区域内流线平行于底板(犁底层)，水力梯度等于犁底层坡度，利用双超模型原理，当犁底层上表面处土壤含水量超过土壤田间含水量，来水量大于犁底层下渗能力，在水力梯度作用下产生横向流动，得到侧向出流模型：

q=iAtanα

(7)

式中：q为侧向出流量(ml)；i为犁底层上表面入渗率；A为出流断面面积(cm2)；α为坡面坡度。公式(7)反映出壤中流侧向出流流量变化过程与降雨强度及土壤初始含水量无关，与犁底层上表面入渗率有关。以上侧向出流模型虽然忽略了侧向出流土壤导水率与犁底层土壤导水率之间的差异，但在重力作用下的垂向迁移能力与相对疏松的犁底层以上土壤水平迁移能力相近，由此认为公式(7)是成立的。

利用RMSE[14-15]评价模型模拟值和试验实测值之间的差异。公式RMSE表示为：

(8)

式中：n为总数据点数；pi为模拟值；oi为实测值。

表1 土壤基本参数

注：表中含水量为重量含水量。

1.2 试验设计

利用自制坡度可调节的集雨槽(长100 cm，宽40 cm，高50 cm)装土，坡度调节范围0°～30°。土槽设计上下2个径流收集口，上侧收集口下边缘低于土面0.5 cm，收集土表径流，下侧收集口位于上侧收集口以下11.5 cm处，收集位于12 cm处犁底层以上壤中流。采用侧喷式人工模拟降雨器(NLJY-09-2型，降雨均匀度系数>0.86，降雨高度4 m)模拟降雨。试验装置见图1。设计坡面坡度7°和10°两个水平，降雨强度0.12 cm/min，土壤初始含水量18.8%，根据取土样地实测犁底层深度及土壤容重，设计犁底层位于土表以下12 cm深处，犁底层以上控制土壤容重1.23 g/cm3，犁底层土壤容重1.38 g/cm3，降雨历时40 min。试验2次重复。供试土壤理化性质见表2。将供试土壤过4 mm孔筛网除去碎石块、植物根茬等杂质，经风干、均匀混合处理备用。利用烘干法测量土壤含水量，计算出达到设计含水量需加水量。将试验用土、水按照重量(利用电子秤称重)平均分成数份，将第一份土壤均匀摊铺在塑料上，土层厚约2 cm，将水按每份重量均匀喷洒在土层上，按重量覆盖上第二层土壤，再喷洒上设计水量的水，如此往复，最后用塑料将土包好，防止水分蒸发。24 h以后打开塑料，将土混合均匀。通过上述方法，可以获得水分与土壤混合均匀的供试土壤，土壤含水量误差可控制在士1%(重量含水量)范围内。将混合好的土壤按设计容重分层装入土槽中，每5 cm为一层，用秤称量土重，装土时用土锤轻轻地将土面砸平，为了得到平整的土面，用锋利的刀将多余土量刮到土少的地方。填装下一层土前抓毛下层土壤表面，以防土层之间出现分层现象。土壤填装完成后用塑料将土槽盖好。装土深40 cm，预留10 cm土槽侧壁防止雨水击溅造成水量减少出现试验误差。约24 h以后开始降雨试验。用容量为2 000 ml的塑料桶在土槽接水口接取地表径流及壤中流，产流后每1 min收集1个水样，停止降雨后在土槽中部沿坡面垂直方向取土壤剖面，收集土样，每10 mm取1个土样。饱和导水率的测定采用环刀法获取土槽试验后原状土，环刀高70 mm，直径50 mm，设3个重复，采用马氏瓶定水头供水测定饱和导水率，取平均值。

图1 试验装置

表2 土壤基本农化状况

2 结果与分析

东北黑土区犁底层普遍存在，犁底层界面以上当土壤含水量超过土壤田间持水量后，在水力梯度影响下产生横向流动，本研究进行的2种坡面坡度试验是模拟野外大田实际犁底层分布情况进行的，壤中流的产生与野外大田实际产流情况较为接近。

通过试验获取壤中流随时间变化过程见图2。随着降雨时间的延续，前期(0～23 min左右)没有壤中流出现，在这一阶段，入渗水仅在重力及毛管吸力等作用下做垂向运动，壤中流产生以后流量随时间推移首先呈增加趋势，然后趋于平缓(图2)，与地面径流变化规律相似。对比坡面坡度7°与10°条件下的壤中流流量变化图，坡面坡度为7°时，壤中流稳定在1.5 ml/min附近，而坡面坡度为10°时，壤中流流量稳定在了2.4 ml/min，坡面坡度是壤中流的重要影响因素。2种处理条件下壤中流产流时间实测值分别为23.3，22.9 min，可见坡面坡度对壤中流产流时刻影响较小，对稳定流量影响显著，2种坡度下壤中流流量均在37 min左右趋于稳定。从壤中流流量过程线可知，关于犁底层以上入渗水未触及犁底层时段，土壤饱和层与集水槽挡板相接触的饱和土壤中土壤水分无水平运移的假设接近实际情况。

对比壤中流模型模拟值与实测值，模型模拟值与实测值基本一致，2种坡度条件下RMSE分别为0.136 ml/min和0.138 ml/min，R2分别为0.89，0.92，模型能够反映出存在犁底层条件下的壤中流产生情况，说明了壤中流水力坡度可以近似认为是地面坡度，同时将犁底层入渗能力作为壤中流计算依据的假设具有一定的合理性。2种处理条件下模拟值均小于实测值，产生这一现象的原因可能是试验过程中出现了边界效应，入渗水沿土槽壁面下渗快于在土壤中垂直下渗速度，使得犁底层以上靠近土槽侧壁土壤含水量高于正常沿垂向土壤迁移条件下土壤含水量，壤中流流量实测值高于模拟值。

图2 2种坡度处理条件下壤中流流量实测值与模拟值

图3为降雨结束后土壤沿垂向含水量实测值与模拟值及犁底层分布位置。2种坡度处理条件下湿润峰下移深度基本相同，可见坡度对土壤垂向入渗影响不显著，2种处理湿润峰均触及犁底层并下移。壤中流的产生是土壤含水量超过田间持水量且入渗受到犁底层明显阻碍后在犁底层表面产生的侧向流动，其对土壤水分的垂直入渗影响很小，土壤水分的迁移仍然以垂直入渗为主，本研究试验采用的土壤容重犁底层以上与农田耕层相同，饱和导水率为0.025 4 cm/min，而犁底层饱和导水率为0.012 0 cm/min，入渗能力减小显著，壤中流流量与垂直入渗量相比较取决于犁底层坡面坡度，我国东北黑土区坡耕地大部分较为平坦，取土样地平均坡度7°，壤中流相对于垂直入渗量较小。虽然图3显示出边界效应的存在，但是模型模拟值与实测值仍然较为接近，2种坡度条件下RMSE分别为1.31%，1.24%(重量含水量)，R2分别为0.94，0.97，说明Richard模型可以反映出东北黑土区坡耕地存在犁底层条件下的土壤水分入渗过程。

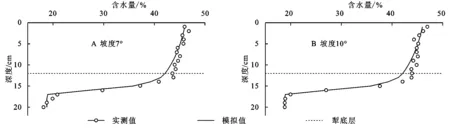
图3 降雨结束后土壤剖面含水量实测值与模型模拟值

图4为2种处理条件下降雨过程中坡面径流过程，两种处理条件下产流时刻较为接近，实测值分别为18.21，17.43 min，可见缓坡对于径流产生时刻影响较小，这一研究成果与Dong等[10]研究成果较为接近。坡度对于随着降雨时间的延续，流量显著增加，2种处理条件下均接近250 ml/min趋于稳定，壤中流流量约为地表径流量1/100，这一比例与降雨强度关系较大，降雨强度越大，比值越小。降雨强度也决定着土壤剖面含水量的变化，降雨强度越大，湿润峰向下迁移越早，壤中流产生时刻越早，使得壤中流流量过程整体前移，形状并未改变。虽然壤中流占径流总量比例较小，但壤中流养分浓度可近似认为是相应深度的土壤水养分浓度，据相关研究显示坡面径流养分浓度较土壤水养分浓度小几个数量级[10]，所以土壤养分的径流流失主要是通过壤中流这一途径。同时，由于壤中流携带养分的水平迁移，也影响了植物根系对土壤养分的利用。

对模型的敏感性分析结果见图5。利用模型分别模拟了不同坡面坡度、土壤初始含水量及降雨强度条件下的壤中流径流过程。各条件下从降雨开始至产流时刻历时见表3。坡面坡度对壤中流产流时刻影响较小(p>0.05)，土壤初始含水量和降雨强度的变化引起壤中流出现时刻的变化，且变化规律与地表径流相似。不同条件下壤中流产流时刻模拟结果较为合理，说明该模型对壤中流产生机理反映接近实际情况。图5A为改变坡面坡度后壤中流过程，坡面坡度对产流时刻影响较小，但对稳定出流流量影响较大，随着坡度增加显著增加(p<0.05)。图5B—5C显示不同土壤初始含水量和降雨强度对壤中流过程稳定出流之前影响较大(p<0.05)，土壤初始含水量越高，降雨强度越大壤中流出流越早趋于稳定，这与不同条件下壤中流出流过程理论分析基本一致，说明模型对不同影响因素较为敏感，同时说明模型能够较为合理的反映壤中流出流过程。

图4 2种坡度处理条件下降雨过程中坡面径流过程

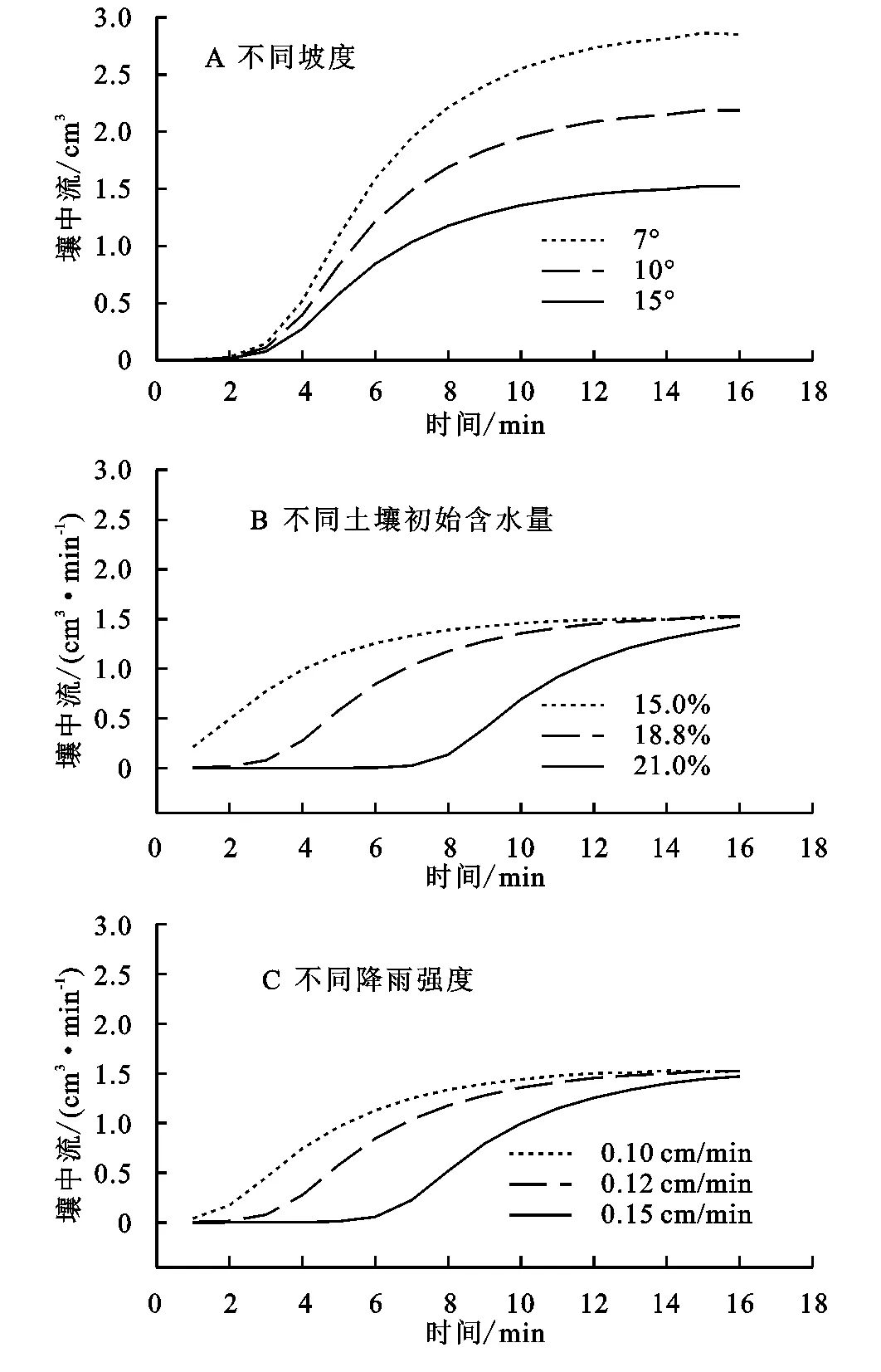
图5 模型模拟不同坡度、初始含水量及降雨强度条件下的壤中流过程表3 不同条件下壤中流模型模拟产流时间

3 结 论

犁底层的存在导致壤中流的产生，土壤质地一定条件下，坡面坡度是决定壤中流强度的关键影响因素。随着坡度的增加，壤中流强度增加显著，坡度对于壤中流及坡面地表径流产生时刻影响较小。初始含水量及降雨强度仅对产流时间影响较大，对壤中流流量大小影响较小。降雨强度增加、土壤初始含水量增高均能使壤中流产流时间缩短。壤中流流量显著小于土壤表面径流，但其对土壤养分水平迁移的贡献可能高于土表径流。基于连续模拟犁底层上部土壤及犁底层内部土壤水分垂直迁移的Richard模型，结合动力波模型及“双超”模型原理构建的壤中流水平迁移机理模型能够准确反映黑土区坡耕地壤中流径流过程。这一模型的建立是基于黑土区坡耕地这一特定条件，其他下垫面条件下的壤中流水平迁移模拟适用性有待进一步验证，同时，该模型适用于壤中流流量上升及稳定阶段的模拟计算，对于下降段不适用。