基于24位置的MEMS惯性传感器快速标定方法

孙 佳，邹 靖，胡 桐

(齐鲁工业大学(山东省科学院)，山东省科学院海洋仪器仪表研究所，山东省海洋环境监测技术重点实验室，山东 青岛 266001)

0 引言

微惯性/卫星组合定位系统、鞋绑式微惯性行人室内定位系统的研究及应用都依靠微机电系统(MEMS)惯性传感器提供重要信息[1-4]。但MEMS惯性传感器自身存在更大零偏、噪声、标度因数、非正交误差且具有温度差异[5-7]。标定是确定误差参数补偿并提高数据精度的重要手段，利用传感器输出与参考信息进行比较,从而确定各项误差参数[8-9]。传统标定方法借助速率转台提供可靠的方向及旋转角速率作为参考[10-12]。通过设置合理的转停方案，该类方法能以较高精度估计出惯性传感器的各类误差，但传统基于转台的标定方法存在设备昂贵以及操作流程复杂等弊端，且无法实现系统的现场标定。

本文设计了一套无需借助高精度转台设备的MEMS IMU快速原位标定方案。该方法将惯性测量单元(IMU)固定于六面体夹具内放置在平面上，以IMU不同放置方向静止阶段重力信息标定加速度计误差，以相邻静止阶段的旋转角度标定陀螺仪误差。一次数据采集即可完成加速度计与陀螺仪的标定，简化了标定流程，减少了标定时间且不影响标定精度。

1 三轴加速度计标定

1.1 加速度计误差模型

受制造工艺及使用条件变化等影响因素，三轴MEMS加速度计各轴可能不严格正交，即存在非正交误差[10]。非正交误差成因示意图如图1所示，图中xs、ys、zs为加速度计各敏感轴，xb、yb、zb为运动载体坐标系的三轴，θij(i、j=x,y,z)是失准角，表示加速度计第i敏度轴围绕载体第j坐标轴的旋转。

图1 非正交误差成因示意图

θij一般为小角度，因此，考虑小角度，假设可以得到加速度计输出由b系变换至s系的转换矩阵[13]：

(1)

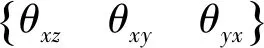
(2)

(3)

为简化标定模型，式(3)未考虑MEMS加速度计噪声，噪声影响可通过对一段时间内的原始数据求平均的方法消除。

1.2 MEMS加速度计标定方法

将式(3)中涉及的加速度计9个误差参数整理为向量形式：

(4)

加速度计第k次输出模型可改写为关于误差参数向量X的函数：

(5)

加速度计的标定以重力矢量为参考信息，静止状态下，加速度计只受重力矢量影响，其3个轴向输出信息的矢量和应与重力矢量相同。将IMU按不同方向放置并保持静止，能够完成各轴加速度计标定。定义代价函数：

加速度计标定即确定X的最优估值满足代价函数F(X)最小，即

(7)

式中F(X)为非线性函数。式(7)为非线性优化问题，本文采用牛顿法迭代计算：

(8)

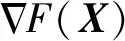
由式(8)可知，每一步迭代都使代价函数减小，可设置当‖Xk-Xk-1‖小于给定阈值时停止迭代。为防止牛顿法迭代收敛到局部极小值点，需要精心设置误差参数向量的迭代初始值，使其尽量靠近全局最优解。采用简易六位置静态标定方法确定迭代初值，将IMU放在平面上，依次使其三通道加速度计大致处于竖直方向，分别近似指向重力方向及其反方向。加速度计零偏、标度因数的迭代初始值可近似计算为

(9)

2 三轴陀螺仪标定

2.1 陀螺仪误差模型

与MEMS加速度计数据输出特性相似，MEMS陀螺仪同样包含零偏、标度因数和非正交误差。考虑到当前三轴陀螺仪都集成在同一芯片上，各轴向非正交误差远小于零偏、标度因数、陀螺漂移及噪声等引起的误差[14-15],因此，三轴陀螺仪输出误差模型可表示为

ωb=Kg(ωs-ε)

(10)

式中：ωb为载体系下角速率信息；ωs为陀螺仪各轴向实际输出；Kg为由kx、ky、kz组成的陀螺仪对角阵；ε为由εx、εy、εz组成的陀螺零偏向量。

2.2 MEMS陀螺仪标定方法

MEMS陀螺噪声大，无法有效测量地球旋转角速度，因此，MEMS陀螺的标定需要外界提供有效输入。标定时，由IMU静止开始绕陀螺仪某一轴旋转指定角度,然后静止，则该阶段由陀螺输出计算的角度变化Δθim可由下式计算：

(i=x,y,z；m=1,2,…,n)

(11)

式(11)可改写为线性方程Ax=b形式,其中

(12)

(13)

(14)

陀螺仪输出计算所得转过的角度Δθ与IMU真实转过角度的误差为e(x)=Δθ-b。

陀螺仪标定即求x的最优估计，使误差e(x)最小，即

(15)

由最小二乘理论，使式(15)误差取得最小值的x为

x=(ATA)-1ATb

(16)

式(16)包含2个未知参数，因此，对单一轴向陀螺仪进行标定只需2次以上的旋转即可完成。

3 实验结果与分析

根据文中第1、2部分给出的MEMS IMU标定方法，利用一个正六面体夹具对实验室自研MEMS IMU进行标定。IMU采用Bosch公司的BMI055，尺寸为3 mm×4.5 mm×0.95 mm，采样率为100 Hz,其主要参数如表1所示。六面体夹具(见图2)是为了便于陀螺仪标定中实现IMU绕指定敏感轴转动指定角度。

表1 IMU主要参数

图2 实验设置

标定时，首先将IMU固定在六面体夹具中心，分别让IMU各轴依次指上再指下，在每个位置静止一段时间，依据静止阶段重力敏感轴输出，并利用式(9)快速估计加速度计近似零偏和标度因数误差。将非正交误差的初始值取0，得到X迭代初始值：

(17)

确定X的迭代初值后，按图3所示24位置IMU旋转顺序依次旋转IMU，设置采样率100 Hz采集传感器输出数据。IMU在每个位置静止5 s，然后按图中指定旋转轴平稳转至下一位置。IMU共经历24个不同位置，23次旋转，共耗时约5 min。每次旋转角度固定为90°，24位置包含了加速度计三轴分别指上和指下，23个旋转也包含了陀螺仪分别绕其三轴正向和反向旋转。按相同方式独立采集10组数据分别用于实验验证。

图3 IMU 24位置及旋转顺序示意图

采集数据后提取所有静止阶段加速度计输出数据，按牛顿法迭代估计加速度计误差向量；提取旋转阶段对应敏感轴陀螺仪输出数据，按最小二乘法估计该轴陀螺仪误差参数。加速度计10组独立标定实验均值及标准差如表2所示，陀螺仪标定实验均值及标准差如表3所示。

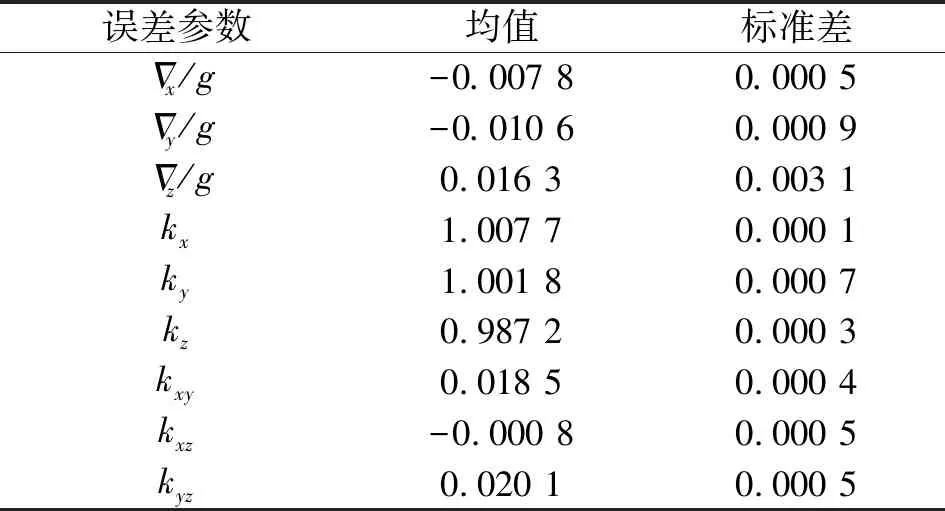
表2 加速度计标定结果

表3 陀螺仪标定结果

续表

误差参数均值标准差ky0.984 50.001 7kz0.947 70.002 1

利用加速度计标定结果分别补偿IMU在24个位置处的加速度输出，得到补偿前、后的加速度模值如图4所示。补偿前，加速度模值波动较大，标准差为0.019 1g；补偿后，加速度模值稳定在重力加速度模值附近，标准差降低至0.001 7g。

图4 补偿前、后的加速度模值

获得加速度计、陀螺仪标定结果后，将IMU转回到初始位置(见图3位置1)并保持静止，此时，IMU中z轴敏感重力矢量，x、y轴处于近似水平面内。设置采样率100 Hz、采集1 min的IMU输出数据，利用表2、3得到的标定结果分别对加速度计和陀螺仪输出进行补偿，得到补偿前、后的加速度计、陀螺输出信息对比结果，如图5、6所示。由图可见，补偿后的x、y轴加速度输出稳定在0附近，z轴加速度输出稳定在重力加速度模值附近。补偿后的陀螺仪三通道输出都稳定在0附近。

图5 加速度计输出补偿结果

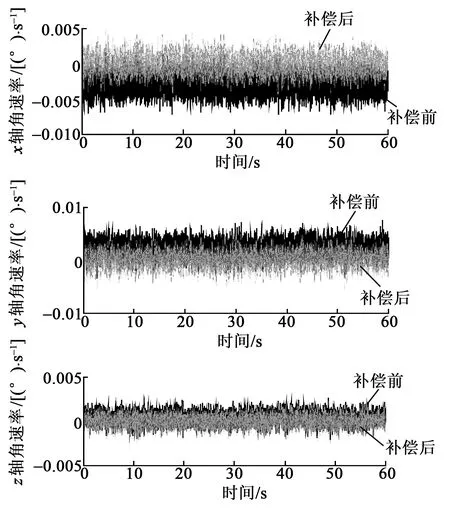
图6 陀螺仪输出补偿结果

4 结束语

MEMS IMU正式应用前需要对其进行误差参数标定与补偿以确保输出数据的精度与可靠性。本文在分析MEMS加速度计、MEMS陀螺仪输出特性的基础上设计了一套无需借助高精度转台的MEMS IMU快速原位标定方案，该方法利用一个正六面体夹具设计24位置连续转停方案。利用牛顿迭代法估计加速度计零偏、标度因数和非正交误差共9个误差参数，利用最小二乘法估计陀螺仪零偏和标度因数6个误差参数。对实验室自研MIMU进行标定补偿实验，结果表明，提出的MEMS IMU快速原位标定方法得到的误差参数能有效补偿各轴传感器误差，提高了IMU输出数据的精度，对实际应用具有一定的参考价值。