基于蒙特卡罗方法的LED芯片定位系统误差分析

龚时华，周迪一，王子悦，李德龙

(华中科技大学 机械科学与工程学院，湖北 武汉 430073)

0 引言

作为第四代绿色照明光源，LED具有能耗低,光电转化效率高,亮度高,使用时间长等优点，已广泛用于交通信号灯、液晶屏背光源、汽车用灯、广告显示等场所。随着LED产能需求的不断扩大，LED芯片分拣机也在不断改进[1]。在芯片分拣过程中，最关键的步骤是对芯片的定位。由于分拣芯片的尺寸变化、运动平台的高加速度启停导致运动过程中的变形、光照环境等变化直接影响了定位精度与分拣效率[2]。

芯片的定位过程包括图像处理[3-4]、运动控制[5]和标定[6]3部分。通过分析各部分的误差，完善误差分配机制，是提升LED芯片定位精度的重要部分。文献[7]建立了6个坐标系，进行多次线性变换，建立光电平台到世界坐标系的模型，分析了7个测量变量与光电平台测量精度误差之间的关系，但无实验测量误差的随机分布状态。文献[8]采用多因素分析方法得到空间直角坐标系到光电传感器坐标系的映射关系，保持其他误差不变，通过修改一个误差值，计算最终定位误差得到误差敏感度，该方法适用于误差因素较少的情况，对于较多误差因素的分析，计算工作量较大。文献[9]对双目视觉动态定位进行了误差分析，先根据误差变化规律将误差分为系统误差和随机误差，再通过统计方法对两种误差进行了定量分析，但未针对具体的误差因素做出分析。文献[10]主要阐述了定位误差的来源和产生过程，但只定性地分析了定位误差。

本文建立了视觉坐标系到目标坐标系的数学模型，根据误差分布情况，采用蒙特卡罗分析法[11]估算最终定位误差，得到每个误差因素的敏感度。根据影响因子的大小进行误差分配，补偿主要误差，提高芯片分拣机的最终定位精度。

1 视觉反馈定位系统

视觉反馈系统由图像采集系统、图像处理系统和运动控制系统3部分组成，如图1所示。由CCD相机拍摄照片，图像采集卡将图像信息传输到上位机进行图像处理，再由上位机发送运动控制指令至运动控制卡中，伺服电机驱动滚珠丝杠实现芯片的定位。

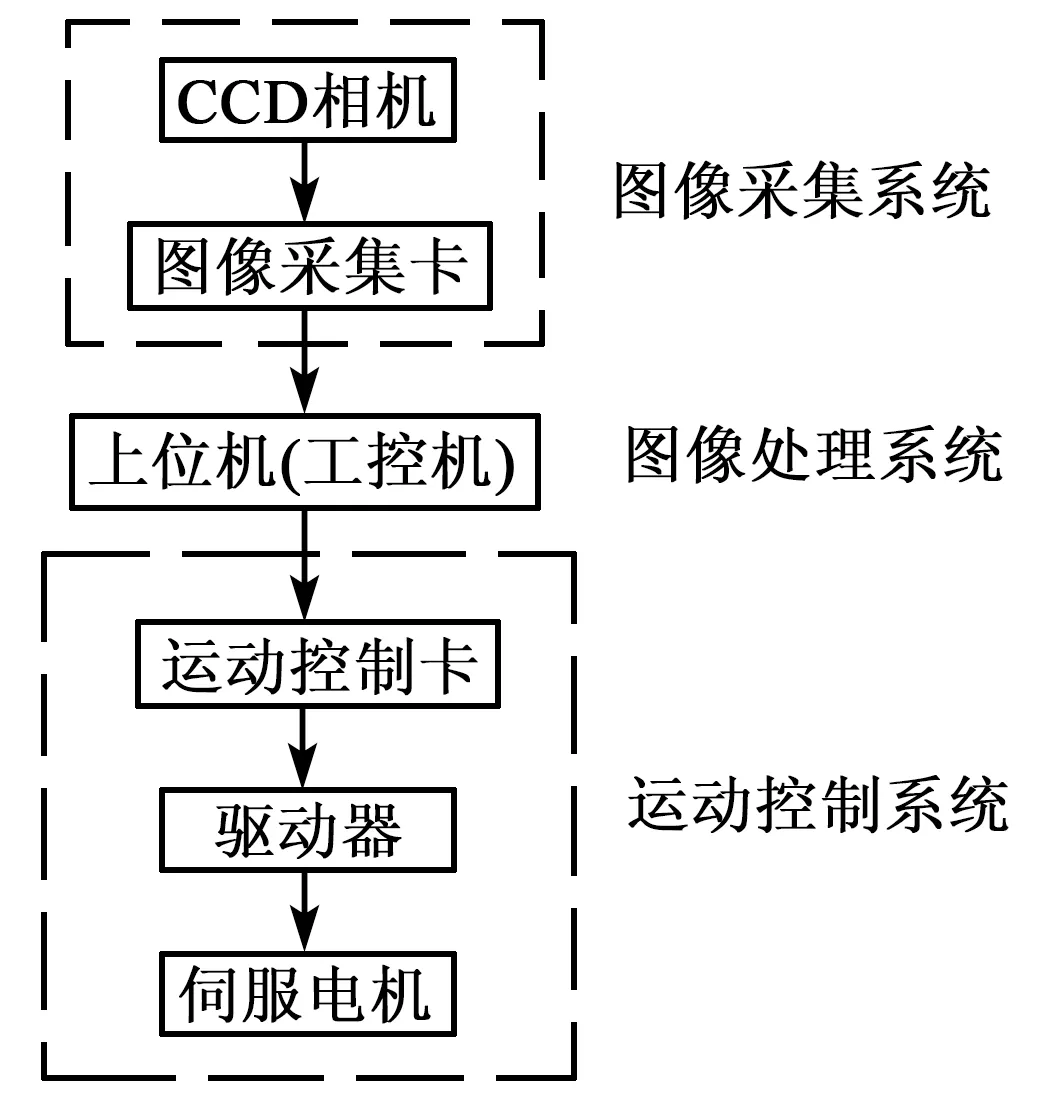
图1 闭环控制系统

1.1 图像处理过程及系统误差

1.1.1 图像处理过程

图像算法过程直接影响着芯片定位的精度，其主要分为亚像素边缘的提取和模版匹配两部分。获取图像进行预处理后，通过最小外接矩形得到芯片的外轮廓，并采用改进的Canny算子来提取芯片亚像素边缘轮廓，最后通过拟合亚像素的边缘轮廓，得到芯片的中心。根据得到的模版进行匹配，选取芯片中心作为特征点进行定位，图像处理过程如图2所示。

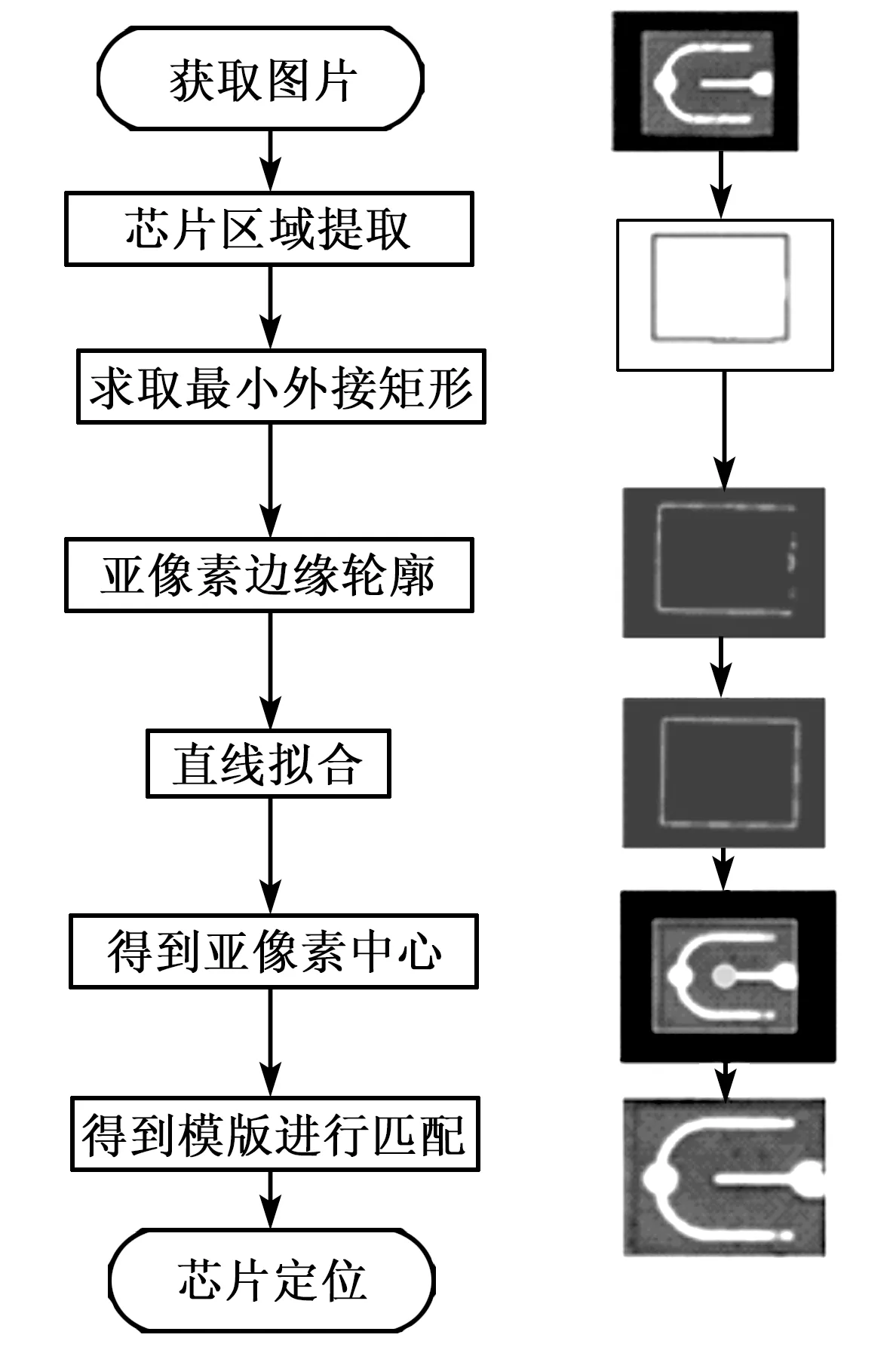
图2 图像处理过程

1.1.2 图像系统误差

图像的系统误差主要来源于图像算法、环境扰动和噪声。为了检测图像误差，设计了如下实验。在保持平台稳定的情况下，对芯片进行重复拍照，记录其中一颗芯片的像素坐标，检测芯片定位的重复度。实验结果如图3所示，经计算得到x、y轴的重复性精度分别为±0.09 pixel、±0.15 pixel。

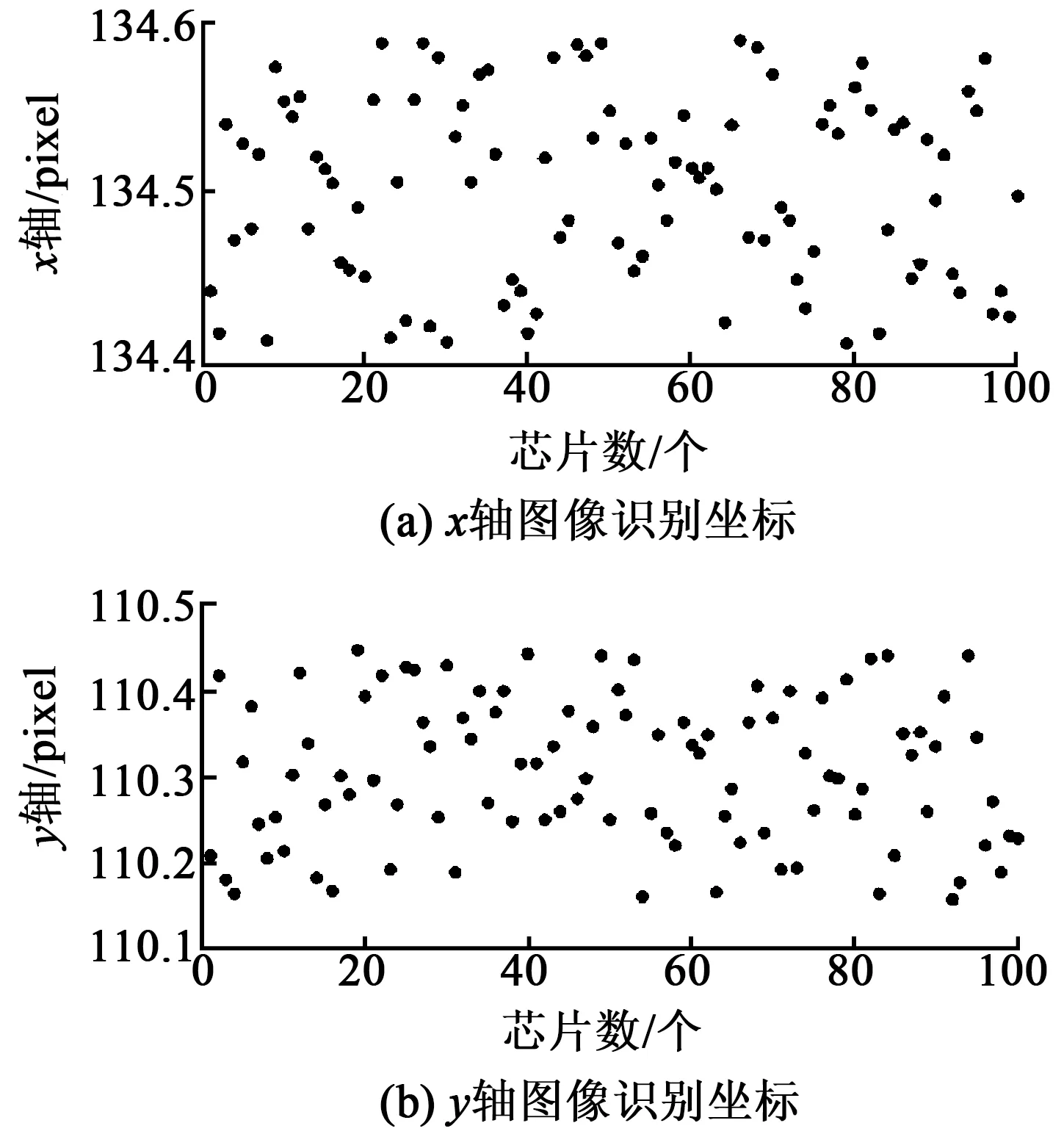
图3 图像识别的芯片像素坐标

1.2 运动控制过程及系统误差

1.2.1 运动控制过程

运动控制系统包含一个电机驱动和2个AC伺服电机，由滚珠丝杠驱动XY二维平台带动芯片移动(见图4)，平台最大速度为500 mm/s。平台定位过程采用粗-精两步定位方法，给定进给量之后，通过编码器反馈进行快速进给，再通过视觉反馈补偿误差完成精确进给。系统控制框图如图4所示。

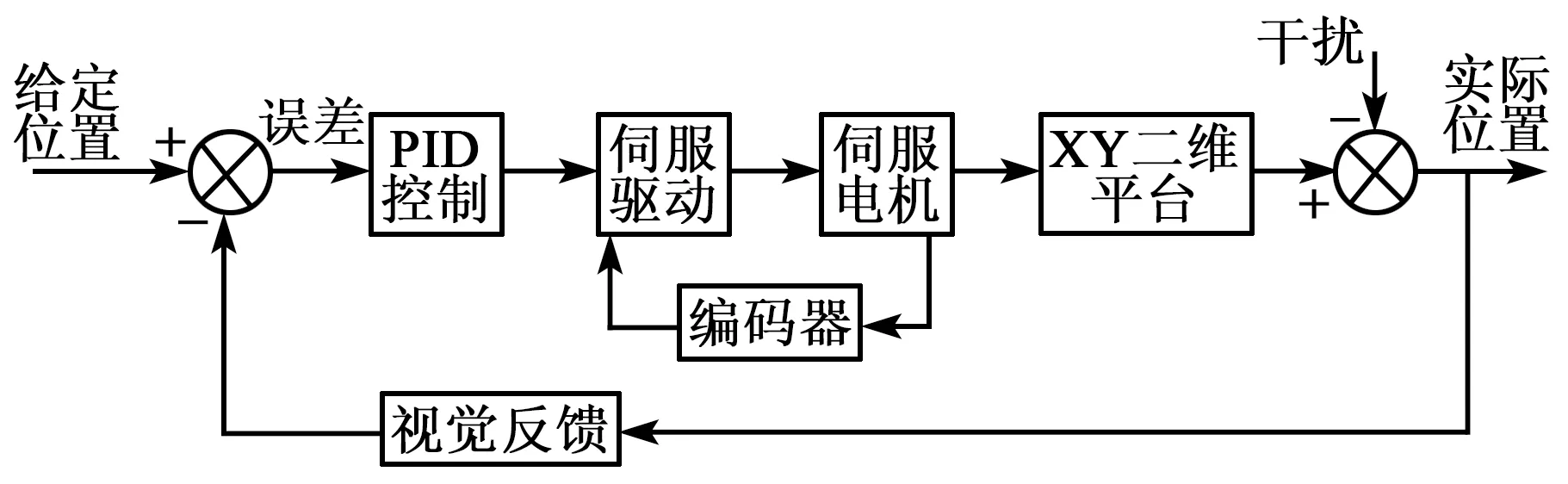
图4 控制系统框图

1.2.2 运动控制误差

运动控制部分误差包括控制系统的稳态误差及滚珠丝杠的定位误差，芯片定位过程中，运动最大位移为1.2 mm。运动控制卡给电机发送2 mm的运动指令，用激光位移传感器测量2个轴的实际位移，重复10次实验，结果如图5所示，得到运动控制误差为±2 μm。

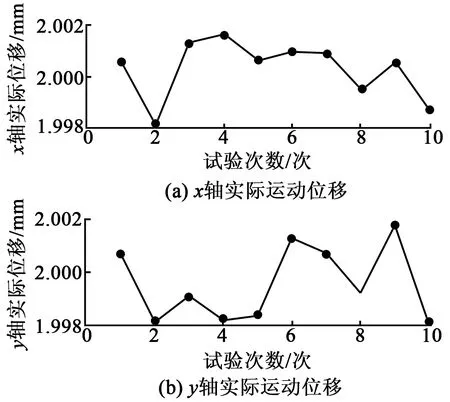
图5 实际运动位移

1.3 坐标变换

为了构建相机坐标系到芯片坐标系的目标定位数学模型，需求解坐标变换中的旋转矩阵。本文主要分析α、β、γ角度误差带来的定位误差，如图6所示。

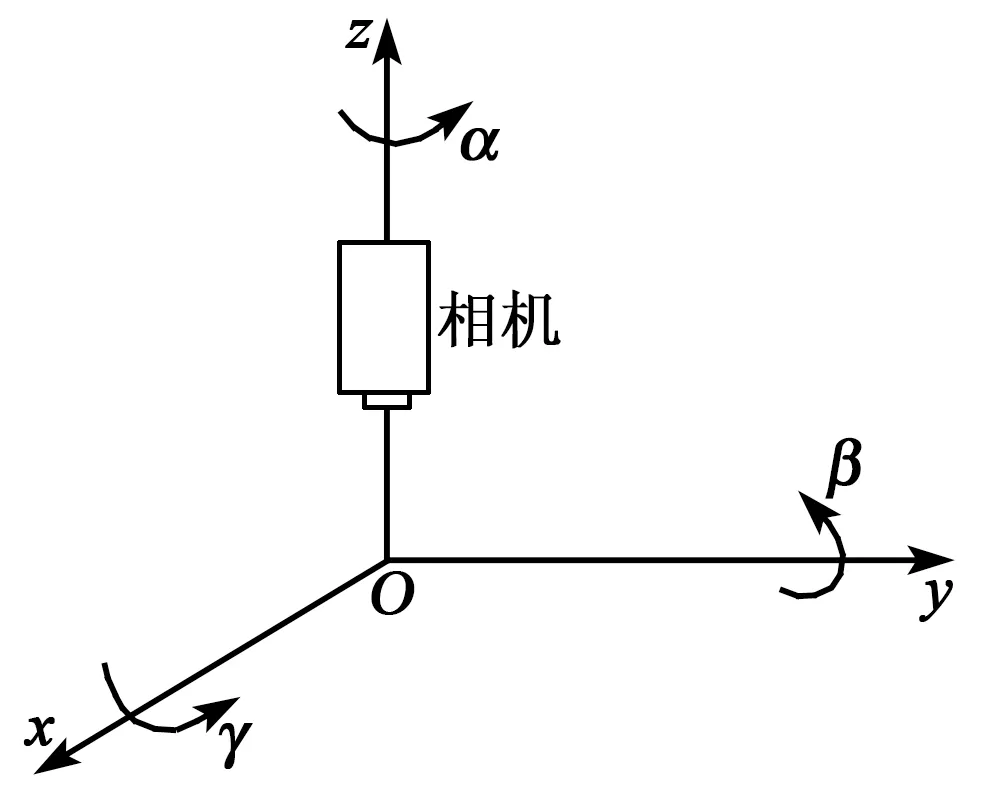
图6 角度偏差

1.3.1z轴旋转

当相机绕z轴旋转α角后，在相机平面内从O1点移动到A点，x、y轴分别移动AB2、AC2，而实际芯片平面内走过距离为AB1和AC1，如图7所示。由相机平面坐标系到芯片平面坐标系变换公式为

(1)

即

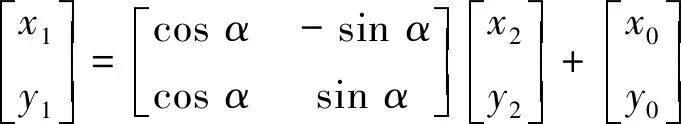
(2)

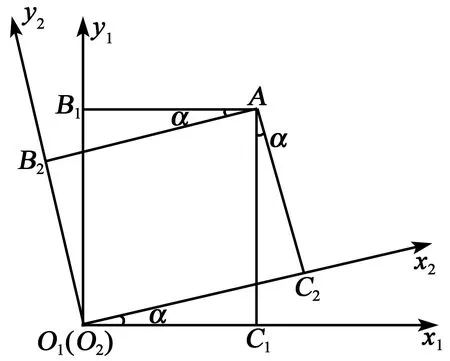
图7 α角偏差

1.3.2x、y轴旋转

图8为β角偏差。由图可见，当相机绕y轴旋转β角后，芯片在相机平面内移动O′B距离时，实际移动的距离为Wx，得到

(3)

同理可得，相机绕x轴旋转γ角后的对应关系为

(4)

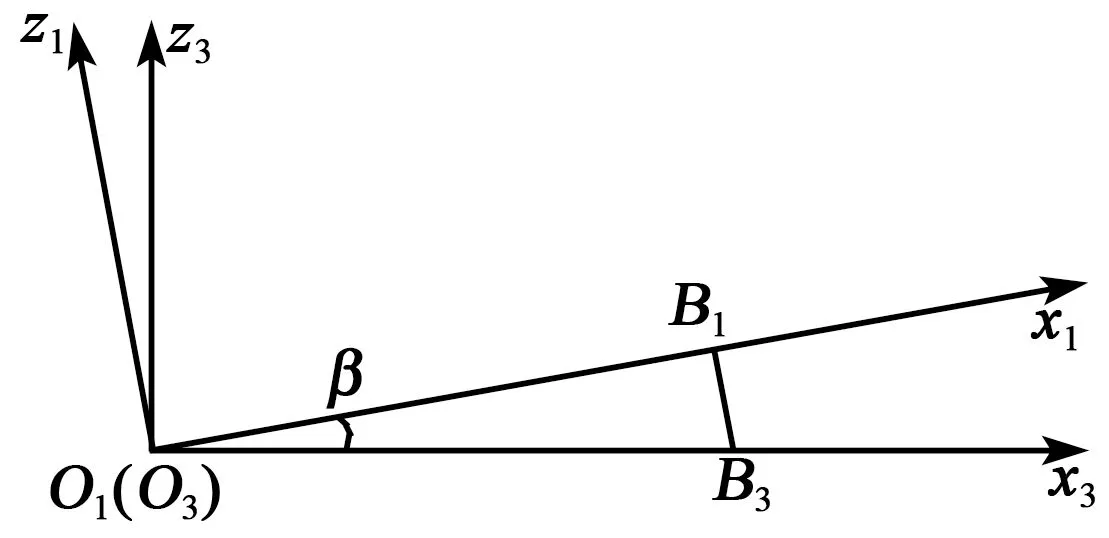
图8 β角偏差

2 误差分析

2.1 误差来源

芯片的最终定位误差包括x、y两轴的误差，与图像处理误差、运动控制误差和α、β、γ角度误差有关，如图9所示。第1节已经提到x、y轴的图像处理误差服从均匀分布，分别为Ux(-0.09,0.09)、Uy(-0.15,0.15)；运动控制误差服从均匀分布Um(-2,2)；α、β、γ角度误差由激光角度仪测得，其中α角服从均匀分布Uα(-0.3,0.3)，β、γ角服从正态分布Nβ(0,0.283 3)、Nγ(0,0.568 7)。

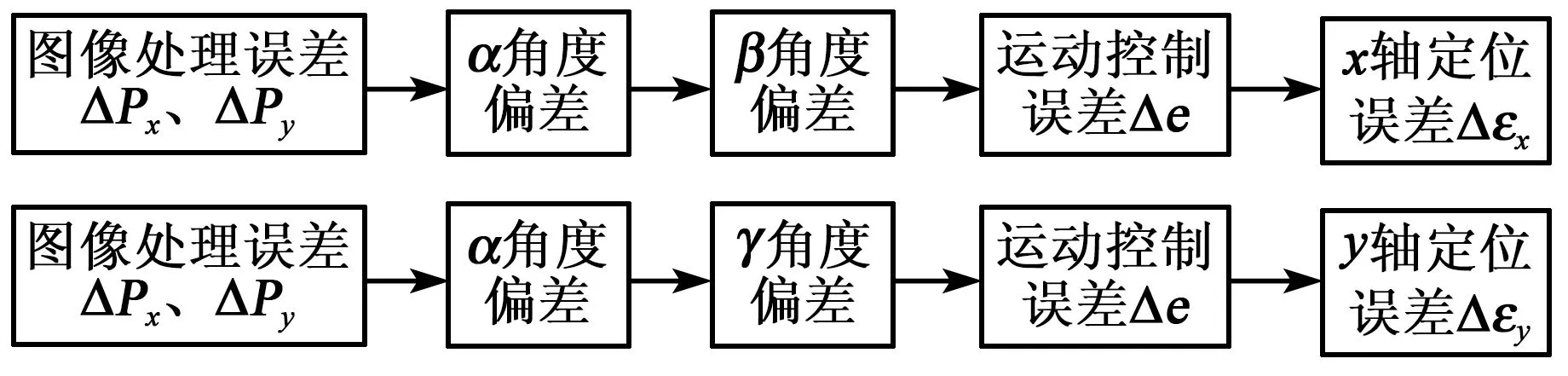
图9 误差来源

结合1.3节可得视觉反馈系统数学模型如下：

(5)

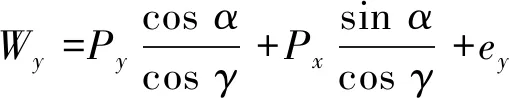
(6)

式中：Wx、Wy分别为芯片实际x、y轴坐标；Px、Py分别为图像x、y轴坐标；ex、ey分别为x、y轴的运动控制误差。

根据图9可得x、y轴定位误差的主要来源。定义目标定位误差分析模型如下：

Δεx=Δεx(ΔPx,ΔPy,Δα,Δβ,Δe)

(7)

Δεy=Δεy(ΔPx,ΔPy,Δα,Δγ,Δe)

(8)

2.2 蒙特卡罗分析法

蒙特卡罗分析法是一种采用随机抽样统计来估算结果的计算方法。其计算结果的精度与抽取样本的数量紧密相关，因此，本实验用Matlab随机生成106个样本进行估算。根据2.1节中各个误差的分布特点，确定了图像处理、运动控制、角度偏差所服从的随机分布，从Matlab中生成的样本进行随机抽样处理，代入式(5)、(6)得到对应的样本值；分别计算出x、y轴定位结果的标准差，代入下式得到误差敏感度(μ)进行分析，分析流程图如图10所示。

(9)

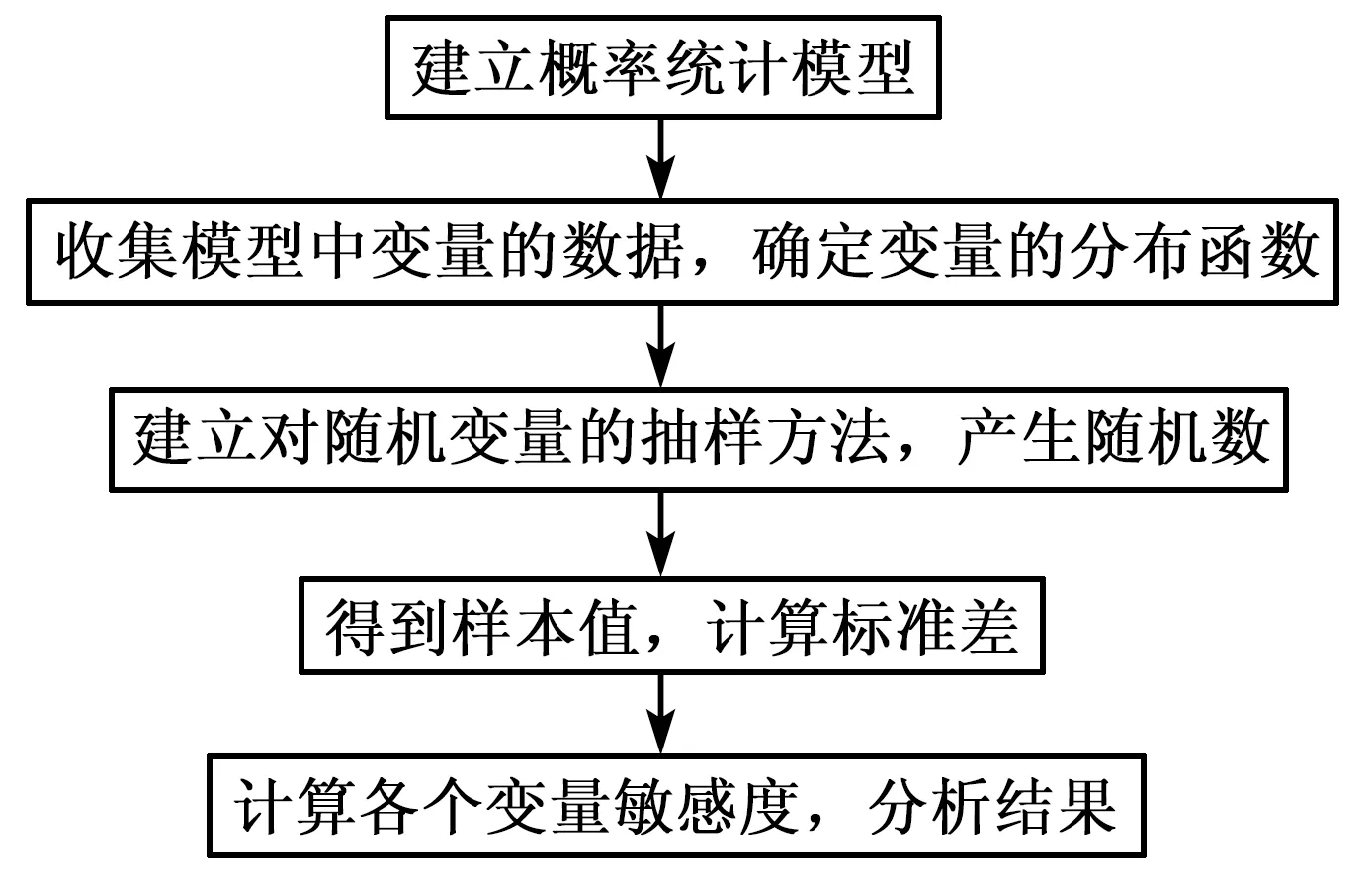
图10 误差分析流程图

当μ<1时，表明该误差变量通过比例缩小传递到最终定位误差，敏感度较低；当μ=1时，表明该误差变量等值传递到定位误差；当μ>1时，表明该误差变量经比例放大到定位误差，敏感度较高。

2.3 分析结果

首先选取一组测量数据进行目标定位计算，通过测量得到相关变量参数如表1所示。将表中数据代入式(5)、(6)，得到对应芯片坐标系中移动距离分别为645.534 1 μm、582.025 9 μm。

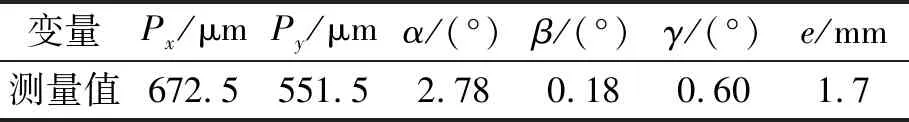
表1 系统测量参数

根据2.2节中的误差分析步骤，将随机生成的106个样本分别将每个变量的随机误差序列与其他变量的测量值组合代入建立的数学模型[12]中，计算对应芯片坐标系中的移动距离，通过式(9)计算得到6个变量的敏感度，计算结果如表2所示。由表可见，运动控制误差直接等值传递到定位误差，通过调节PID参数可减小稳态误差；x、y轴旋转角误差以10-9～10-2的比例作用传递到定位误差，对最终定位精度影响较小；z轴旋转角度误差以约10倍的比例放大至最终定位误差，需通过标定算法来补偿绕z轴的旋转角误差；图像处理过程中的x、y轴误差分别对芯片平台的x、y轴定位误差有一定的影响，需改进图像处理算法，降低图像重复度。

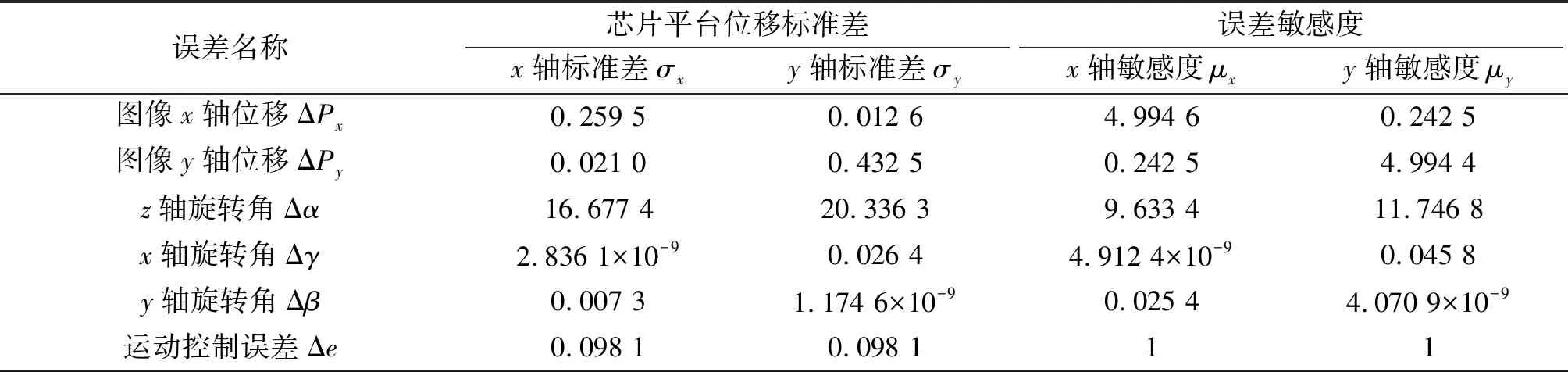
表2 目标定位误差结果

3 结束语

本文根据视觉反馈平台特点，通过分析平台图像处理过程、运动控制模型及安装角度等因素，构建从相机坐标系到芯片坐标系的数学模型。由测量参数的误差分布确定所服从的随机分布，Matlab随机生成106个样本，采用蒙特卡罗分析法来估算目标的定位误差，得到最终定位误差对各个变量的敏感度，对提高系统的定位精度具有一定的理论参考价值。实验结果表明，绕x、y轴的安装角度误差对定位精度影响较小；绕z轴的安装角度误差以接近10倍的比例作用在最终定位误差上；图像处理过程误差以及运动控制误差的敏感度相对较低。因此，通过标定算法补偿α角度偏差带来的误差是提高视觉反馈系统定位精度的关键部分。

本文提出了一种通过蒙特卡罗分析法确定主要误差来源的方法，通过对主要误差进行补偿来提高系统定位精度，为实际应用过程中的误差分配和精度控制提供了一定的理论帮助。