基于同步数字通信接收机的载波频偏补偿算法*
2019-06-25姜宇,王壮
姜 宇,王 壮
(南京邮电大学,江苏 南京 210000)
0 引 言
载波频率偏差估计与补偿是数字通信接收机中的基本问题。由于发送端和接收端振荡器频率不一致产生载波频率偏移(Carrier Frequency Offset,CFO)。CFO是基于数据源与角度随时间成比例的向量相乘得到的,所以CFO对符号解调的影响是累积的,且随数据长度的增加影响更大。CFO除了影响数据的解调,它还影响数据同步,因为前导符号的相关性质在CFO存在时不再成立。估计CFO的典型过程是使用导频来识别接收数据的时段。现有的文献中已经解决了CFO估计与补偿问题,尤其是对于正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)和单载波频分多址(Single-carrier Frequency-Division Multiple Access,CSFDMA)的多载波通信系统。例如,文献[1]提出了一种基于OFDM系统的CFO估计与校正方法。更多关于CFO估计方法可以参考文献[2-6]及其中的参考文献。但是,这些方法的一个主要限制是CFO估计范围受前导周期限制。前导周期越长,CFO估计最大值就越小。在文献[7]中,提出了一种用于Hiperlan/2WLAN的CFO估计与补偿的新算法,其中CFO估计范围扩展到传统解决方案的四倍。但是,它没能解决频偏更大时的CFO估计问题。
本文提出了一种基于定时同步的数字通信接收机中的CFO估计算法。该算法利用任何接收机在采样频率固定时均可获得定时信息的性质,与已存在的算法相比有三个主要优点。首先,该算法不是基于前导符号固定的,因此可以不局限于前导符号的性质进行使用。其次,算法消除了受前导周期影响的CFO估计最大值的限制,这样得出的CFO估计范围远高于固定前导周期的CFO估计范围。最后,该算法展示了有CFO估计过程的定时同步。
本文的其余部分安排如下。第二部分介绍了载波频率偏移的带来的问题。第三部分介绍了定时同步的载波频偏估计算法。仿真结果在第四部分,最后是结论。本文还包含一份附录,详细说明了该文件中提出的一些想法。
1 问题描述
本节介绍了载波频偏估计的问题描述。假设模拟信号方便用于数学描述,使用离散时间来呈现最终算法。让频率为fc的载波信号通过信道传输基带信号x(t),传输信号可以表示为:

假设不存在实际的信道影响和噪声,则可以通过振荡频率f´c对接收信号进行下变频:

其中,HT{x´(t)}表示信号 x´(t)的希尔伯特变换。f´c 是本地振荡频率,可以表示为 f´c=fc+δf,δf是载波频偏。假设基带信号是窄带信号,则(2)也可写成:

在一个典型的数字通信接收机中,载波频率偏移δf是利用接收信号固定时的前导周期得到的。如果前导周期记为T,我们可以得出:
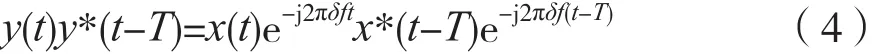
由于前导符号是周期T固定的,我们可以表示x(t)=x(t-T)。因此,可以有:

∠{y(t)y*(t-T)}的范围是 -π 到 +π,因此载波频偏可以由前导周期估计为[-1/2T,1/2T],该范围的大小可能不足以满足标准/应用的要求。考虑到IEEE802.15.4q技术标准[8]的场景,让前导周期为T=32 μs,对应的CFO估计范围为±15.625 kHz,而标准规定的范围为±200 kHz,显然此前导周期达不到这个范围。在接收信号的周期小于标准指定的基本前导周期时,我们有了一个重复搜索的动力。
2 同步载波频偏估计算法
本文提出的算法基于以下事实:利用采样率可以得到时间周期。例如,对于符合IEEE802.15.4q标准的接收机情况下,我们可以针对以下内容进行讨论。假设码片周期1 Mc/s,样本周期Ts=1/8 μs,则过采样率为8。如此,我们可以得到总周期等于nTs,n是一个整数。这将扩大CFO估计的范围,使符合IEEE802.15.4q标准的接收机达到4 MHz(对应于时间周期Ts)。但是,选择更小的时间周期会导致样本间相关性更高,因为他们在时间上靠的很近。这会导致得出的相关角度及CFO估计可靠性降低。利用完整的前导符号或者前导周期的叠加可以解决这个问题。该算法通过以下三个阶段进行。
(1)获得粗分数角Sφ;
(2)基于更可靠的完整前导符号角度Tφ改进粗分数角;
(3)基于可靠的分数角度'Sφ得出CFO估计和同步。
2.1 粗分数角φS估计
接受样本矢量γsamp表示ADC 样本,每个样本记作γsamp(n)。从接受样本矢量中估计CFO随后进行补偿,分数角φS对应于两个相邻样本之间的角度:
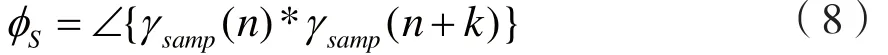
其中,k≥1是整数,与持续时间nTs有关。为了更好的估计,φS的平均值是由一些重复的基本前导符号计算得出。注意,基本前导符号不可谓零直流信号,即在一个完整周期内求和时,前导符号应具有非零平均值。尽管取平均值,分数角的可靠性还是很低,因此我们将该角度称为粗分数角。在下一小节,我们提出了粗分数角的可靠性的改进。
2.2 粗分数角的可靠性改进
对应于完整前导持续时间T的角度也是最大可靠性角度,因为样本最大可能的分开,所以样本之间相关性最小。完整的前导符号角度可由接收信号可得:

此处,P是前导符号长度,角度φT和φS有以下关系:

可靠性改进想法如下。理想情况下,(10)式在n为整数时等号成立,但是,由于噪声以及信道不理想等条件影响下导致角度可靠性的降低,尤其是φS,这将导致n偏离整数值,式(11)中必须使用可靠性更高的的角度φT以及四舍五入n成为整数来恢复这种可靠性。
2.3 CFO估计与同步
从之前获得的角度φ'S,我们可以得到一个基本的CFO估计值:

从这个基本的CFO估计值δf´s我们可以计算出一系列暂定的CFO:

其中,m是一个整数,决定了估计的准确性。m越大,准确性越高,但是代价是计算复杂度的提高。频率fd是一个差异频率,可以定义为:

式(13)~(15)逻辑如下:CFO估计与集合{-m,-m+1,…,m}中2m+1个整数有关,其中一个估计值是正确的CFO,对应的角度将满足(10)等式。假设m=2,则总共可以得到2m+1=5个估计值:
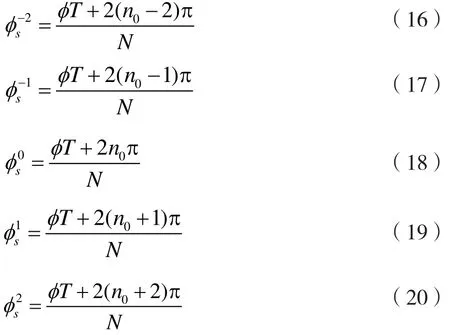
总共得到5个角度,CFO估计值可以计算如下:

式(13)~(15)中的操作相当于进一步提高粗分数角的可靠性,获得了2m+1个可能的CFO估计值h∈[-m,m],用这些可能的CFO估计值来补偿接收样本,这将获得2m+1个补偿向量:

因为其中一个CFO估计是正确的,所以对应的补偿向量将与前导符号产生高相关性。一旦识别出最高相关值的补偿向量,我们就可以获得相应的CFO估计作为最终的CFO估计值。该逻辑用于后续操作。对于每个补偿向量运行滑动窗口算法,其中补偿向量中长度为N的窗口与过采样前导符号结果相关。

这里 Φδfh(k)代表了暂定 CFO 估计的补偿向量相关系数。K是样本数,与前导码周期T有关。序列是通过重复每个前导符号来获得时间上的OSR值。滑动窗口的持续时间取决于预期信号的持续时间。这通常通过传统的分组/能量检测过程来建立。最终的CFO估计通过从2m+1个暂定CFO估计中识别出与补偿向量相关性最高的过采样前导符号结果中得出。此过程可以描述如下:

同步点可以由接收样本的范围索引得到,由此可得到最大相关值。同步索引τ可以由下式得到:

本算法无需任何专门过程即可建立同步。这保证了联合CFO估计和同步。算法的性能还取决于前导符号的相关属性。在没有良好的前导符号时,即使使用较大的m值性能改进的范围也会较少。算法实现的流程图如图1所示。

图1 算法流程
3 仿真结果
CFO估计算法已经在MATLAB 2013b中进行了仿真。出于解演示的目的,实现了符合IEEE802.15.4q 标准的相干接收机。假设符号速率为1 Ms/s,采样周期Ts=1/8 μs,CFO为+200 kHz。考虑两种不同的数据传输模式,即根据标准的2/4-TASK和3/8-TASK,生成图2中的包错误率(Packet Error Rate,PER)与信噪比(SIGNAL-NOISE RATIO,SNR)曲线。

图2 算法仿真
从图2中可以看出,载波频率偏差补偿算法几乎完全补偿了+200 kHz的偏差,从而满足了IEEE802.15.4q标准的要求。在假设中,m的值设置为2。经观察,可以通过增加m的值来实现实际条件的近乎完美的补偿。通过假设条件的研究可以发现增加m的大小可以将估计的性能提高到仅受前导符号相关性限制的程度。
4 结 语
本文提出了基于同步的数字通信接收机的载波频率偏移估计算法。该算法利用分数时间段来获得CFO估计。通过对完整前导符号周期的角度的进行可靠性改进,解决了因更短的时间段而导致的可靠性的降低问题。仿真结果表明,与传统估计方法相比,本算法得到的可估计CFO的范围显着改善,对在前导周期内未能获得符合标准的CFO范围的相位信息场景尤其有用。仿真结果证明了该算法的性能。
