基于小波去噪和改进DCV的脑部MR图像分割

徐 丽，朱家明，李祥健

(扬州大学 信息工程学院，江苏 扬州 225127)

0 引言

一直以来，图像分割[1]都是图像处理领域中很重要的一步。随着科技不断进步，医学影像成为医生后期诊断的重要依据。脑部MR图像[2]因为没有辐射及分辨力高等优点被医学领域广泛应用。但由于设备本身以及外部环境的影响，使得MR图像带有噪声[3]，射频信号不均匀导致MR图像出现灰度不均匀的问题[4]，对后面的临床诊断与治疗造成了影响。

在广大学者的努力钻研下，出现了很多分割方法，水平集方法[5-6]是解决曲线演化课题的经典方法。Mumford-Shah[7]于1989年提出了M-S模型，Chan和Vese[8]于2001年提出了CV模型，传统的CV模型依赖灰度值，对于灰度相差不大的图像很难将目标准确地分割出来。Chan和Vese[9]于2002年提出了多相水平集模型，弥补了CV模型的不足。

1 小波阈值去噪方法

噪声的有效抑制是图像进行分割的基本前提[10]。小波变换[11]以其较好的时频特性在图像去噪领域受到了广大学者的关注。

小波变换的低熵性、多分辨率特性和多相关性[12]使得小波具有去噪功能。首先对观测数据进行小波分解变化：

Wod=Wof+δ·Woz，

(1)

式中，d为观测数据向量，f为真实信向量，z为高斯随机向量。

然后进行门限阈值处理，在式(1)小波系数Wod基础上可获得新的小波系数。阈值的选择很重要，本文采用Donoho和Johnstorn[13]提出的统一阈值：

(2)

式中，δ为噪声标准方差，N为信号的尺寸或长度。

对上面的小波系数做逆变换，得到去噪后的信号：

f*=Wo-1ηλWod。

(3)

基于阈值的小波去噪方法可具体划分为硬、软阈值2种。设w为小波系数，wλ为加入阈值后小波系数的大小，λ为阈值。硬阈值设置为：

(4)

软阈值设置为：

(5)

对于硬阈值会出现伪Gibbss等视觉失真现象，软阈值会引起边缘模糊等失真现象，引用李宏等人[14]提出的改进小波阈值函数，此算法结合了软硬阈值函数的特性，具有更好的去噪效果。

(6)

式中，

(7)

2 双水平集分割方法

2.1 单水平集模型描述

单水平集是将图像划分为目标和背景2相，水平集函数为φ，单水平集区域划分如图1所示，利用水平集函数φ将图像分割成2个互不重合的部分。

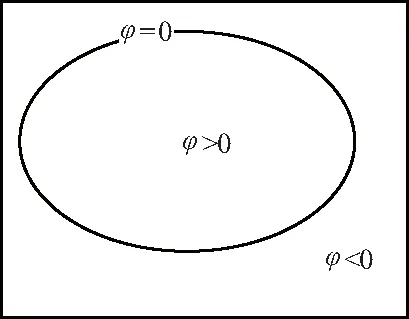
图1 单水平集区域划分图

曲线拟合能量泛函表示为：

E(c1,c2,c)=μ·Length(c)+

λ1∬Ω1(u(x,y)-c1)2dxdy+

λ2∬Ω2(u(x,y)-c2)2dxdy,

(8)

式中，μ，λ1，λ2为正常数，表示各能量项的权重系数，采用水平集φ后能量泛函为：

E(c1,c2,φ)=μ·Length(φ)+
λ1∬Ω1H(φ)(u(x,y)-c1)2dxdy+
λ2∬Ω2(1-H(φ))(u(x,y)-c2)2dxdy,

(9)

式中，H(*)为Hesviside函数。

求E关于c1的一阶偏导数再令它为0，可求得c1，c2用同样方法得到：

(10)

根据Euler-Lagrange方程进行求解，可求得水平集函数φ演化方程为：

(11)

2.2 改进后的水平集模型描述

由于单水平集只能将图像划分为目标和背景2相，适用不广泛。Chan和Vese提出了多相CV模型，即可通过n条水平集函数将图像分割成2n个互不重合的部分。

4相CV模型原理图如图2所示，利用水平集函数φ1，φ2将图像分割成Ω11，Ω12，Ω21，Ω22四个区域，它们之间互不重合。

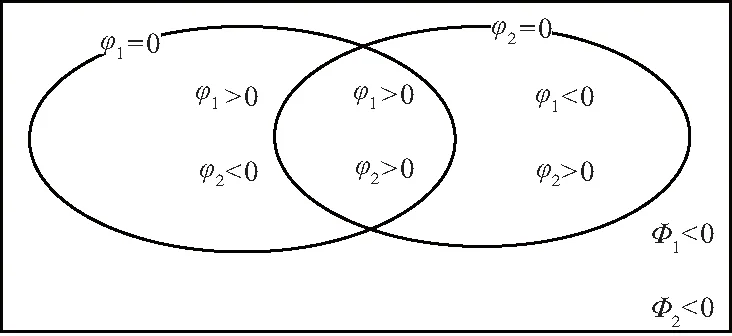
图2 4相CV模型原理图

定义能量函数如下：

(12)

式中，c11，c12，c21，c22分别对应Ω11，Ω12，Ω21，Ω22各区域的灰度均值，可用上述同样的方法求得：

(13)

对于演化过程中出现的重新初始化[15]问题，在能量函数中增加能量惩罚项p(φ)解决，表达式为：

(14)

则新的能量函数可更新为：

E=E(c,φ)+vp(φ)，

(15)

式中，ν为能量惩罚项的系数。在不考虑图像数据项的作用下，根据Euler-Lagrange方程和梯度下降流，最终的水平集函数φ1，φ2的演化方程为：

((u-c11)2-(u-c12)2H(φ1)-((u-c21)2-

(u-c22)2(1-H(φ2))]+

(16)

((u-c11)2-(u-c12)2Hε(φ1)-((u-c21)2-

(u-c22)2(1-H(φ1))]+

(17)

2.3 算法流程

算法流程如图3所示。先加载出要处理的图像，再用小波阈值去噪算法进行预处理，最后用改进后的DCV分割算法对处理过的图像进行分割，得到最终的分割图。

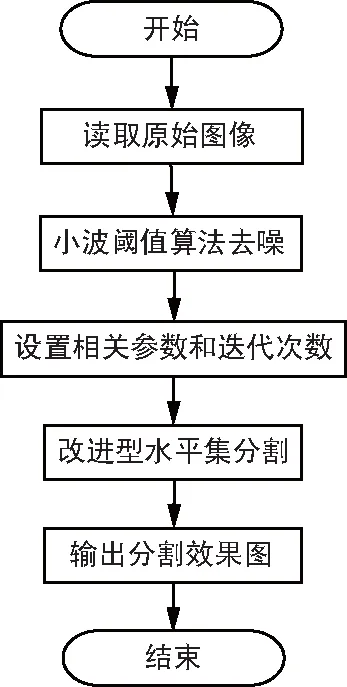
图3 算法流程

3 实验结果与分析

本文实验环境：Matlab 2014a，Windows7，PC，CORE i5-3230M，CPU 2.60 GHz，4.00 G RAM。

实验中需要设置的相参数为：λ1=1,λ2=1，ν=1，μ=0.001*2552，时间步长Δt=0.01，水平集函数迭代次数为30次。

本文选取了2张脑部MR图像进行去噪预处理。本文去噪算法和其他去噪算法的效果对比如图4所示。由图4可以看出，传统的去噪算法会使图像变得不清晰，去掉了很多细节信息，而本文去噪算法有更好的效果。

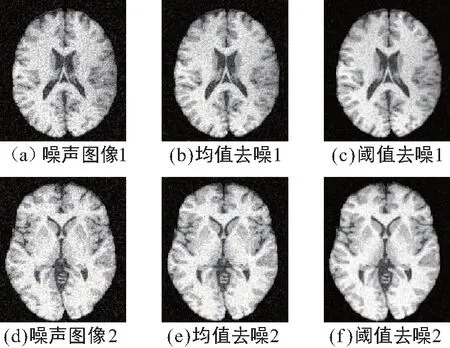
图4 不同算法去噪效果对比图

分别用传统DCV模型和本文改进后的模型来分割去噪后的图像，效果如图5所示。

采用Jaccard Similarity(JS)指标进行比较分析：

(18)

JS值越大表明效果越好，本文算法与传统DCV算法的JS指标如表1所示，可看出本文的算法分割效果更好。

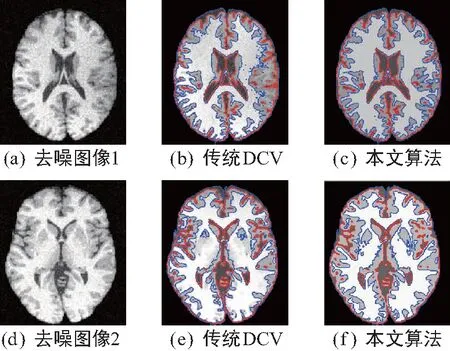
图5 医学MR图像分割效果对比图

表1 2种算法的JS指标

图像组织分割算法DCV本文医学图像1白质0.750.89灰质0.700.86医学图像2白质0.760.90灰质0.750.84

4 结束语

本文利用基于阈值的小波变换先进行去噪，对图像进行预处理，既很好地保留了信号细节，同时又拥有较好的去噪效果。并在传统DCV中通过在能量函数中增加能量惩罚项解决曲线在演化过程中重新初始化的问题，提高了计算速度。实验表明，该模型可以较好地分割含有高噪声、灰度不均和多目标问题的脑部MR图像。