多目标救灾应急物资调度优化问题研究

孙欣欣 李珊红

(合肥学院计算机科学与技术系， 合肥 230601)

救灾应急物资调度是应急管理工作的重要环节，直接关系到救灾工作的效率。及时而有效地将灾区急需的各种应急物资送到各个受灾点，可以减少甚至避免人员伤亡，降低灾害可能带来的损失和影响。因此，救灾应急物资调度与普通的物资调度不同，它对物资调度方案的合理性、科学性有着更高的要求。具体来讲，就是要使救灾物资在尽可能短的时间内运达灾区，分配的物资要能够最大程度地满足各个受灾点的需求，同时还要考虑将调度运输成本尽可能控制在合理范围内。这是一个对多个目标进行优化的问题。

20世纪90年代以来，许多学者对此问题进行了研究。甘勇等人以最小化运输成本和时间成本的总和为目标，建立了混合整数规模模型，并设计了一种启发式算法对模型进行求解[1]，但他们的研究只是针对单个受灾点的情况。胡飞虎等人针对多供应点、多受灾点的应急物资调度问题建立了模型，并运用遗传算法进行求解，但他们只研究了运输时间最小化的单目标优化问题[2]。本次研究，将探讨在一次性消耗条件下，涉及多个储备库、多个受灾点、多种应急物资的复杂问题组合优化调度方案，在应急物资需求种类及数量约束下，构建基于运输时间最短、出救储备库最少的多目标调度模型，并基于遗传算法进行问题求解。

1 应急物资调度问题建模

1.1 问题描述

针对多储备库、多受灾点、多种应急物资的情况，定义如下变量：

N个储备库，S={A1，A2，A3，…，AN}；M个受灾点，D={D1，D2，D3，…，DM}；K种物资，G={G1，G2，G3，…，GK}。w为一种物资的分配方案，w={wrpq}N×M×K，wrpq表示储备库r到受灾点p调度物资q的数量。

灾区应急物资调度问题的目标是运输时间最短、出救应急点最少。此问题还涉及满足以下约束条件：每个储备库的所有物资的分配量，均不得超过其储备量；各个受灾点得到的所有物资的数量，均能分别满足其需求量。因此，可以建立如下数学模型：

s.t.

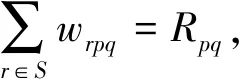
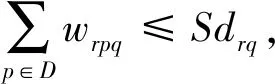
wrpq≥0,trp≥0,∀r∈S,∀p∈D,∀q∈G

Sdrq≥0,∀r∈S,∀q∈G

(1)

其中：Sdrq表示储备库r中物资q的存储量；Rpq表示受灾点p需要的物资q的数量；trp表示储备库r运输物资到受灾点p需要的时间。

1.2 问题转化

讨论解决的应急物资调度问题是多目标优化问题，即要求运输时间(Tw)最短、参与救灾的物资储备库(Nw)最少。为方便求解，需要将多目标优化问题转化为单目标优化问题。我们采用理想点法进行问题转化。

按照理想点法的原理，先要找出评价目标函数的最劣值和最优值，也就是负理想点和正理想点。在求最优解时，计算各个方案与正理想点和负理想点的相对接近值。与正理想点越接近，则说明该方案越接近最优解[3]。

定义Rv和rv分别为目标函数的正理想点和负理想点，则

(2)

(3)

其中：w1和w2分别表示物资运输时间及参与救灾的储备库数量的权重，两者之和等于1。由于在此问题中，两个目标同等重要，所以将w1和w2都设置为0.5。从以上公式可以看出，当Tw和Nw越小时，则Rv越大、rv越小，hv也越小。hv=(Rv+rv)Rv。由此可以将原来的多目标问题转化为以下单目标问题：

min{hv}

s.t.

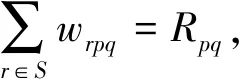
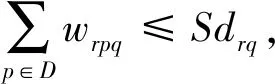
wrpq≥0,trp≥0,∀r∈S,∀p∈D,∀q∈G

Sdrq≥0,∀r∈S,∀q∈G

(4)

1.3 约束条件处理

在本问题中，约束条件包括等式约束和不等式约束2种情况。需要将这些复杂约束条件进行处理，并将其体现在目标函数中。我们采用惩罚函数法进行约束条件处理。

按惩罚函数法的原理，当某个方案不满足约束条件时，就在目标函数中为其添加一个惩罚项，使该方案对应的目标函数值变得极差，进而将该方案淘汰[4]。

本问题有2个约束条件：每个储备库的所有物资的分配量，均不得超过其储备量；各受灾点得到的各种物资量，均满足其需求量。以xrpq表示储备库r发送给受灾点p的物资q的数目，2个约束条件对应的惩罚函数分别为g1(x)和g2(x)。

(5)

(6)

其中：L=100，代表惩罚系数。

对带约束条件的多目标问题，利用理想点法和惩罚函数法进行问题转化和建模，得到以下目标函数：

(7)

通过以上方法，便将求解基于约束条件的Tw和Nw最小值的问题，转化为求解f(x)的最大值问题，使复杂问题得到了大大简化。

2 基于遗传算法求解

遗传算法是求解最优化问题的经典算法，它通过模拟自然界生物优胜劣汰的进化机制，寻找适应度最高的最优解[5]。

针对应急物资调度问题，建立的适应度函数公式：

(8)

利用遗传算法求解应急物资调度问题，步骤如下。

采用实数编码，初始化种群中的染色体：

(i=1,2,3,…，Sw)

(9)

第2步：开始迭代。迭代次数Set_iter=100 000。

第3步：选择。采用轮盘赌法进行染色体选择。每个染色体被选中的概率与其适应度有一定关系，但并不是说适应度函数值高就一定会被选中，适应度函数值低就一定不会被选中，选择过程中存在一定的随机性。按轮盘赌法原理，根据每个染色体的适应度大小，画出一张圆盘。适应度越大的，在圆盘上所占的角度和面积就越大。每次通过转动轮盘，选出一个被保留的染色体。多次操作之后，选出新的被保留的种群。这种算法既考虑到了每个染色体的适应度的大小，又保留了一定的随机性。

第4步：交叉。采用中间重组交叉算子完成染色体交叉。将所有染色体分成若干组，每组包含2条染色体。在每组染色体上，随机选择需要进行交叉的基因位置。在需要交叉的同一基因位置上，对应的2个基因进行交叉重组。

第5步：变异。采用非均匀变异算子。每条染色体随机选择需要变异的基因位置，将该基因在其取值范围内重新随机生成一个新的基因，完成变异。

第6步：检查染色体合法性。检查每条新的染色体是否符合本问题的等式约束条件和不等式约束条件，如果不符合约束条件，则根据约束条件重新调整染色体的值。

第7步：迭代结束。如果满足收敛条件或达到最大迭代次数，运行结束，输出结果。

3 实验结果

实验运用2009年我国多个地震灾区的应急物资调度数据。通过建模和求解，得到救灾应急物资分配调度最优方案。在该问题中，储备库数量N=16，其编号由A到P；受灾点数量M=5，需要的物资种类K=5。已知每个储备库中所有物资的储存量、每个受灾点对每种物资的需求量、每个储备库到各个受灾点的运输时间。应急物资调度方案要实现的目标为：从储备库到各受灾点的运输时间最短、参与救灾的储备库数量最少。这是典型的多目标优化问题。

原始数据量太大，在此不便一一列出。以应急物资中的帐篷为例，运用遗传算法求解。每个储备库需要向每个受灾点运输的帐篷数量如表1所示。

根据上述建立的模型，通过遗传算法求解。按照计算的结果，在所有可行方案中，最优方案是：需要参与救灾的储备库数量Nw=8个，最少运输时间Tw=2 960 min。

4 结 语

救灾应急物资调度安排问题，在多储备库、多受灾点、多种类物资的情况下，是一个典型的多目标优化问题。其中，要求实现的主要目标是参与救灾的物资储备库最少和物资运输过程中花费的时间最少；同时要求符合2个条件，即每个储备库的所有物资的分配量不得超过其储备量，每个受灾点得到的各种物资量均能够满足其需求量。对此，我们采用理想点法将多目标问题转化为单目标问题，采用惩罚函数法对约束条件进行处理，完成了建模，并给出了利用遗传算法进行求解的步骤。本次研究提出的多目标救灾应急物资调度模型及求解方法，适用于大规模突发的多目标、多约束条件的灾区物资调度问题，有助于提高救灾效率。