立足思维起点,领悟假设精髓
2019-06-21徐莉娇
徐莉娇

[摘 要] 新课改后,高中数学增加了“几何概型”内容,它是有关概率的一种计算方法,对于高中生对概率概念的深入理解,以及在现实生活中如何计算事件概率有着很好的帮助. 通过“几何概型”来强化高中生的数学思维,领悟数学思想方法大有裨益. 文章结合教学实践,对此进行了详细阐述.
[关键词] 高中数学;“几何概型”;假设;数学思维
新课改对高中数学教材进行了一系列改革,部分新内容作为对高中数学知识体系必要的、有益的补充被添加进来,这些内容对于高中生更好的探索数学本质,加强數学与生活之间的联系发挥着重要作用,其中具有代表性的就是“几何概型”. “概率论”是高中生在数学学习中必须要学习和掌握的一项重要知识,但概率概念相对抽象,且很多高中生对于如何应用数学知识计算现实生活中事件发生的概率并不擅长,所以在古典概型的基础上,引入了“几何概型”模型. 高中生在学习古典概型之后会形成简单的“概率思维”,所以在学习“几何概型”时难免混淆,其原因在于高中生的数学思维尚不成熟和严谨,对数学思想方法没有一个深入的了解与掌握. 故在“几何概型”的教学中,应立足学生思维起点,领悟数学思想方法精髓,帮助学生建立起数学与生活的联系,让他们学会如何运用数学方法去认识和改变生活. 本文以“假设”思想为切入点,对“几何概型”教学中数学思想方法的渗透与实践进行了全面解析.
[?]“假设”,从问题情境中开始
在高中数学教材中,“几何概型”的概念是通过实例向高中生进行描述的,然后给学生介绍了随机模拟方法,让他们掌握到计算“几何概型”问题的一种方法. 在教材中的例题较有代表性,且通俗易懂,利于教师开展教学. 该节课的教学重点是让学生掌握计算方法,难点在于如何将未知量求解问题转化成“几何概型”概率求解问题. 因此在突破重点与难点时,可以有效渗透“假设”方法与思想,通过“问题情境”的创建,引导学生进行自主思考与探究,寻找到解决“几何概型”问题的有效方法,培养他们科学的数学思维方法.
如在进行“几何概型”概念讲解前,先给学生出示问题组:
(1)取一根绳子,长度是3米,拉直后选择任意一个位置剪断,求剪断后得到的两根绳子的长度大于或等于1米的概率;
(2)张文和李松两人一起玩转盘游戏,如图1所示,如果指针停留于B区时张文胜;反之李松胜,求张文胜出的概率;
(3)将一探测器置于某个空的长方体房间的屋顶,该探测器的探测范围呈现圆锥状,如果有不明物飞到这个房间,假设它在房间任意角落均有悬浮可能,那么探测器探测到该不明物的概率有多大?
面对三个貌似毫不相关的问题,怎样让学生将其联系起来,并从中总结“几何概型”概率问题的解决方法?教师可以引导学生通过假设、猜想进行上述问题的解决:假设三个问题之间存在着某种共同点,那么大家是否可以对三个问题的概率进行猜想?不是让学生去直接面对问题,而是通过假设和猜想让学生自主探究隐藏于问题背后的数学本质,这对于学生是一种全新的学习方式,因此他们也会投入十分的热情. 最后通过问题分析,就能够得出“几何概型”公式:P(A)=(D的测度≠0).
“假设”是一种引导学生从另一个角度去看待问题,尝试着从原有问题中“再生”出新的问题,并通过大胆猜想、小心求证对新问题进行分析、理解、解决,体验问题解决多样化策略,发展学生创新与实践精神的数学思想方法. 它淡化了传统教学过于形式化、机械化记忆的弊端,重视学生在问题情境中对知识的体验与理解,它更关注学生运用数学思维去领悟知识形成的过程,也促进了学生在“几何概型”学习中的自主性,培养了他们探索新模式,发现新规律的数学能力.
[?]“假设”,在生活情境中深化
任何一种思想与方法,都需要在生活实践这个“土壤”中,才能真正地生根发芽. 在上述的问题情境创建中,由于隐藏于问题中的数学本质相对浅显,接受起来学生还是感觉很容易,但因为浅显所以在对“几何概型”的理解上也会存在表面化的现象,之所以会增加“几何概型”的相关内容,除了提高学生的数学思维之外,更重要的还是让他们体验数学知识的实用价值,即学会运用“几何概型”知识去解决现实中与概率相关的问题. 所以在问题情境设计之余,还要通过生活情境让学生如何将数学知识以及“假设”的数学思想方法运用于现实中去. 如给出一个生活化问题:“甲、乙两人要在六点到七点之间到某地碰面,但因为各自都有事情未解决,因此提前告知对方无论谁先到达指定地点都给对方预留出十分钟的等待时间,如在十分钟内另一个仍未到则先到者可以先行离开,那么两个人会面概率有多大?”像这样一个约会和等待的问题,几乎每个学生都有类似经历,但是可能很少有人想到要用“几何概型”去计算概率,所以生活化的问题一出,学生们倍感兴趣,认识到了这种计算方法可以有效地节省彼此的时间. 但显然这种生活“味儿”太浓的问题,很短时间内学生无法与之前的数学问题联系起来,这时就可以用“假设”的方法引导学生:“假设该问题与之前问题之间存在本质上的联系,是不是可以考虑用‘几何概型方法进行解决?”这种假设就是将生活与数学连接在一起,让学生找到思考的方向,沿着这个思路再次审题,他们就会从“等可能性”的角度去寻找其中隐藏的一些数学条件. 而在解题中同样可以运用“假设”方法进行巧拨妙引:“假设两人能够见面,那么它的前提条件是什么?”在这样的引导下学生展开分析,问题就变得简单多了:
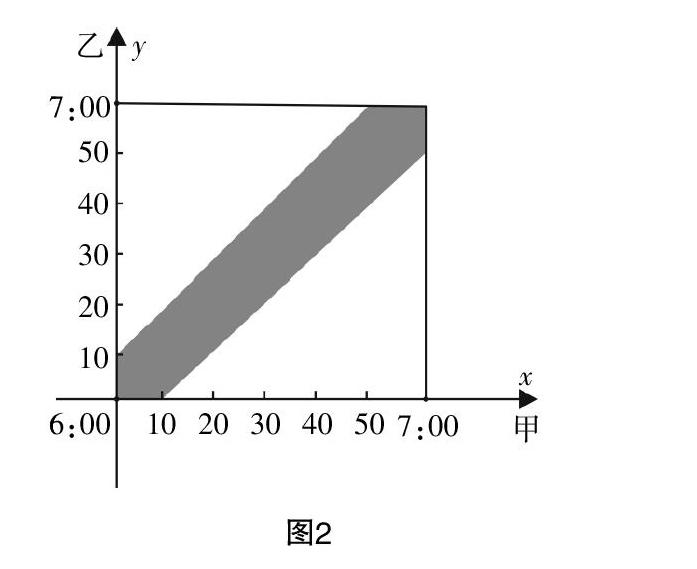
两人到达约定地点的时间相对任意,无论是甲还是乙,只需要在六点到七点之间任意时间即可,这样就会有无数个结果产生,那么就找到了题目中有两个变量(连续型)存在,甲和乙两人到达约会地点的时间,即x,y. 那么用坐标表示就会出现图2. 所有(x,y)点最终形成了正方形一个区域,因为到达时间是存在随意性的,所以正方形区域内的点都存在等可能性,假设该问题与之前问题本质一致,那么可以列入“几何概型”范围. 假设两人正常会面的前提条件是“甲先到达后乙在规定十分钟也到达”,由此推出x-y≤10. 这时鼓励学生将自己之前学过的“线性规划”与之结合到一起,在图中描绘出满足该条件的存在于直角坐标系中的所有点,用阴影表示,最后得出:P(A)=. 在这种相对复杂的现实问题中,关键是让学生掌握到解题的正确方法,通过建模、假设,将生活化问题转化为“几何概型”数学问题,再利用公式进行求解. “几何概型”与“几何”是并不存在直接关系的两个概念,只是因为在现实生活中一些相关问题能够以“几何图形”的形式进行描述,再用几何知识加以解决. 现实生活中凡与概率相关的问题,均能够用“几何概型”进行解决,但关键是如何找到“几何概型”的特点与本质.
无论是建模、假设、猜想、转化,都是数学思想方法的重要内容,在“几何概型”教学中,这些思想方法都不会是独立存在的. 领悟假设精髓的过程,就是渗透数学思想方法的过程,而在高中数学学习中,掌握到了数学思想方法的内涵,就等于站在了数学思维的最高点.
