无标度网络上具有病毒变异的SIAS传播模型

2019-06-21董晶徐浩刘文瑾柳雄顶长江大学电子信息学院湖北荆州434023

长江大学学报(自科版) 2019年5期

董晶，徐浩，刘文瑾，柳雄顶 (长江大学电子信息学院，湖北荆州 434023)

人类面临的各种疾病突发事件越来越频繁，如禽流感病毒(H7N9)、乙肝、SARS等传染病突发事件[1～6]。尽管人们采取治疗药物控制了疾病病毒的传播[7～10]，但在传播过程中病毒易发生变异，从而增加了病毒传播的复杂性。当病毒发生变异后，原有的抗病毒药物可能失效，在新型抗病毒药物产生之前，变异病毒会导致疾病爆发，而新抗病毒药物产生之后，疾病的传播会被抑制[11]。对上面2种传播特性，建立适当的传播模型来研究疾病的传播机制将有助于了解疾病的传播动力学行为，从而采取有效的措施来抑制疾病的蔓延[12～14]。文献[15]提出了一类SEIR传染病模型，研究了在均质网络中病毒变异前恢复率对疾病传播的影响。文献[11]提出了一类SIS传染病模型，研究了在均质网络中的病毒变异后出现的一段真空期对疾病传播的影响，研究结果表明真空期的出现能增加瞬间感染比例，而对稳态感染比例没有影响。但这些基于均质网络上的研究，未考虑疾病网络的无标度特点[16]。考虑变异行为对疾病传播的影响和网络的无标度特点，笔者提出了一类无标度网络上具有病毒变异的SIAS传播模型。

1 模型建立

图1 SIAS模型的流程图

SIAS模型流程图如图1所示。假设系统由3类节点组成，分别为易感染节点(S)、感染节点(I)和变异节点(A)。S类节点与I类节点接触后以概率ρ1转变为I类节点，S类节点与A类节点接触后以概率ρ2转变为A类节点；r表示变异率，即I类节点发生变异转变为A类节点的概率；α、β分别表示I类节点和A类节点的治愈率，即转变为S类节点的概率;θ1、θ2分别表示S类节点与I类节点和A类节点的接触概率。

令Sk(t)、Ik(t)、Ak(t)分别表示t时刻在度值为k(k=1,2,3,…,n)的节点中易感染、感染、变异节点所占的比例，根据平均场理论，建立如下传播动力学方程：

(1)

式中：Θ1(t)、Θ2(t)分别表示t时刻随机取一条边与感染节点或变异节点相连的概率：

(2)

2 模型分析

基本再生数表示一个患病者在平均患病期内所传染的人数[17]。

定理1令基本再生数：

当R0<1时，系统(1)存在无病平衡点E0(1,0,0)；

(3)

由方程(3)可以解得：

(4)

由方程(4)可得：

(5)

(6)

将方程(6)代入方程(2)得到：

(7)

可得：

即基本再生数满足：

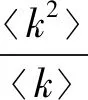
3 数值仿真

假设网络规模N≈1000，平均度值k≈6，各类节点的初始值为Sk(0)=0.9,Ik(0)=0.1,Ak(0)=0。

选取参数ρ1=0.25,ρ2=0.2,r=0.2,α=0.75,β=0.8时，R0=0.7554<1，系统(1)中S100,I100,A100随时间t的变化趋势如图2(a)所示。从图2(a)可以看出，R0<1时，稳态I100、A100均趋于零。表明病毒在网络中将会逐渐消失，系统稳定于无病平衡点。

选取参数ρ1=0.5,ρ2=0.2,r=0.2,α=0.6,β=0.5时，R0=1.9829>1，系统(1)中S100,I100,A100随时间t的变化趋势如图2(b)所示。从图2(b)可以看出，R0>1时，稳态I100、A100分别趋于正的稳定值，表明病毒在网络中将会持续存在，系统稳定于地方病平衡点。

选取参数ρ1=0.5,r=0.2,α=0.6,β=0.5，ρ2依次取0.3、0.2、0.001，稳态(I100+A100)随时间t的变化趋势如图3所示。从图3可以看出，减小ρ2值，稳态(I100+A100)会降低,表明减小变异病毒的感染率ρ2可以降低疾病的稳定值大小。

选取参数ρ1=0.5,ρ2=0.2,α=0.6,β=0.5，r依次取0.15、0.2、0.4，稳态(I100+A100)随时间t的变化趋势如图4所示。从图4可以看出，增大r值，稳态(I100+A100)会降低。表明在病毒变异后能及时开发出新型抗病毒药物的情况下，即β>0，增大病毒变异率r有助于控制疾病的传播。

选取参数ρ1=0.5,ρ2=0.2,α=0.6,β=0，r依次取0.15、0.2、0.4，稳态(I100+A100)随时间t的变化趋势如图5所示。

从图5可以看出,稳态(I100+A100)会趋于1，且r值越大，趋于稳定的时间越短。在病毒变异后未能及时开发出新型抗病毒药物的情况下，即β=0，r增大，即使不会改变最终患者及变异人数，但在短期内会稍微增大患病规模。