基于应力不变量的多轴疲劳寿命预测方法
2019-06-21李雪夫
李雪夫,宋 宇
(中车建设工程有限公司,北京 100000)
0 前言
多轴高周疲劳从研究以来,还没有一种对各种材料、各种载荷普遍适用的多轴高周疲劳失效准则。
本文将剪应力等效幅值的求解过程与损伤估算相联系,通过考虑载荷偏量路径沿求解剪应力等效幅值时的参考坐标系各轴投影的分量来估算疲劳损伤。在此基础上,对疲劳损伤和平均应力的关系进行了充分考虑。并将静水应力时间与各个投影路径载荷时间有机结合起来,为对应区间内静水压力最大值、主计数通道相关循环辐值的计算提供了有利条件,利用修正S-N曲线方法来估算每条投影路径损伤,最后通过等效推导并结合修正S-N曲线估算总损伤与疲劳寿命。
1 基于应力不变量的剪应力等效幅值的求解
要想获得剪应力等效辐值,需要明确材料平面上的应力。如果材料平面上一点处的应力在受到多种循环荷载作用时,其应力为Sn,为了体提高剪应力等效幅值计算效率,需要合理采用分解法,将Sn应力分解成两部分,其分别是切应力和法向应力,这两个应力分别用τ、σn来表示,如图1所示。

图1 复杂周期载荷作用下材料平面上应力参量的演化
材料表面的一处应力在复杂循环载荷作用下,会发生相应的变化。其矢端在空间中形成一条闭合曲线Φ是最主要的变化之一。在这种情况下,剪应力也会随之变化,一般情况下也会在在材料平面上也形成一条闭合曲线Ψ。这两条曲线具有一定的关联性,都属于材料平面上的投影。其中曲线Ψ主要是由选取过这一点的材料面决定的。材料平面上一点在某一时刻的剪应力为τ(t),剪应力矢端在材料平面上的质点和轨迹分别是点O′和Ψ。在这种情况下,剪应力向量O→A可视为向量OO→′与向量O′→A的合成。O′A的模定义为该时刻剪应力的幅值,记做τa。OO→′的模定义为该时刻剪应力的均值,记做τm。裂纹成核主要是由材料平面上的最大剪应力幅值决定的。根据塑性力学的相关理论,切应力幅值τa的值可以用应力偏量第二不变量的值替代,对于比例载荷可以通过定义式求得,但实际遇到的载荷大都为非比例的,因此可以求解偏应力第二不变量的等效幅值替代 τa。
为了简化计算过程,定义一组映射关系:

经过上述变化,偏应力张量Sij由6维降至5维,变成5维空间里的一个向量Si,并且有
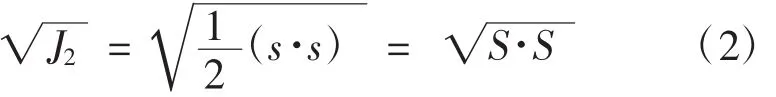
由此可得,在数值上,等于应力偏量Sij虽然发生了变化,但其第二不变量的平方根与Si的2范数是一致的。
疲劳损伤与载荷幅值的方差有关[1]。为了使剪应力等效幅值的求解物理意义明确,在应力偏量空间中建立根据载荷幅值的方差所确定的参考坐标系对其进行求解。在变换后的5维空间中,求出应力偏量向量的协方差

其中:

求出该协方差阵的特征值及其特征向量。要想对这5个特征向量进行全面的了解,不仅要结合特征向量的几何意义,而且还应该明确特征值。在整个一基础上,可以认识到这5个特征向量能够在某种程度上反映协方差矩阵的空间性质。在该过程中,应该注意,及时坐标发生了变化,其特征向量和特征值也不会发生变动。要想知道参考坐标系是否是唯一的,需要合理建立参考坐标系E0,进而明确其是唯一的。
如果荷载路径沿着坐标系E0进行投影,通过对求各个投影路径进行观察和分析可知,其所有路劲都属于时间函数。在本文为中,主要是对一段二维偏量空间中的偏量载荷路径进行了分析。如图2所示,是其主要的投影过程。

图2 投影过程示意图
通过上述方法确定的参考坐标系,在对投影过程分析的基础上,可以了解载荷幅值对疲劳损伤的影响。所以在进行损伤估算过程中,也需要借助上面所建立的参考坐标系。在进行计算时,其主要分为两大步骤。第一步,进行多段单轴载荷历程引发的损伤估算;第二步需要合理计算总损伤,也就是由原载荷导致的所有的损伤。但是要想提升在复杂载荷作用下,疲劳损伤估算的准确性,还需要对载荷循环对应时段内平均应力所造成的损伤进行分析,了解其实际产生的影响。为了实现良好的损伤估算效果,该过程需要对两段载荷时间历程进行同步计数。文献[2]提出了一种多轴循环计数方法,可以实现载荷的同步计数。利用该方法计出每条投影路径载荷历程下每个全循环的应力幅值。这条载荷路径水应力作用和载荷路径幅值的作用水平分别用平均值个和投影路径下幅值的平均值进行表示。
剪应力的等效幅值为

2 基于应力不变量的多轴疲劳寿命预测模型
根据Summel提出的修正S-N曲线方法[3],建立基于剪应力等效幅值的双对数坐标下的修正S-N曲线,等效剪应力幅值,如图3所示。
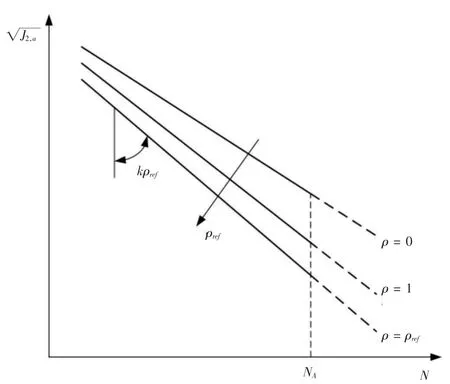
图3 基于应力不变量的修正S-N曲线
考虑了平均应力与载荷非比例因素,通过静水应力的平均值σH,m与剪应力的等效幅值的比定义修正系数ρref

对于任意载荷条件下循环次数为NA次的ρref和k(ρre)f值的获取可以通过拉伸与纯剪应力状态时材料常数的线性组合,因此可以表示为:

根据相对Miner原理和疲劳损伤线性累积准则,任意条路径的总损伤为

定义一条等效路径,i条路径只有一个载荷循环,与总损伤处于一致状态。这条等效路径的应力幅值为
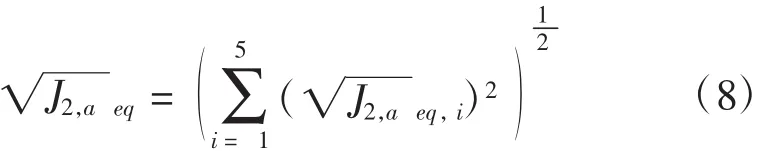
如果将等效路径应力幅值函数当作总损伤,其应该表示为:
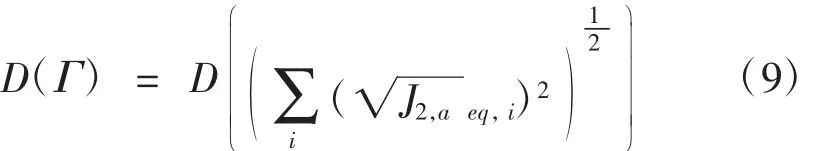
根据修正S-N曲线(如图4所示),利用Miner原理求解多轴复杂载荷作用下的总损伤。

多轴复杂载荷作用下的疲劳寿命为
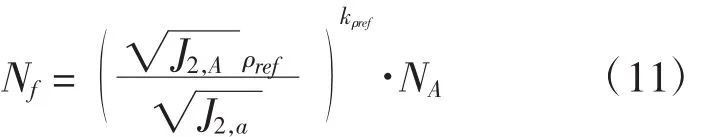
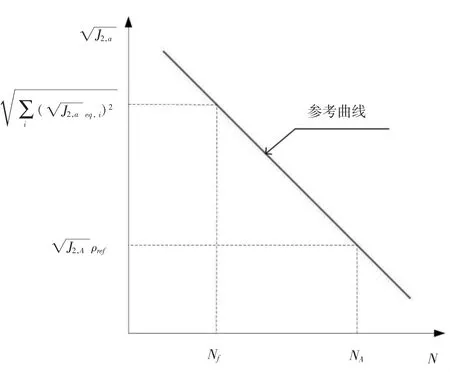
图4 多轴疲劳寿命估算的修正S-N曲线
3 试验验证
选用45#钢 、30NCD16钢进行结果验证,试验数据选自文献[4,5]。材料的相关力学参数参见表1,本文寿命预测模型的相关的材料常数参见表2。寿命预测值和试验结果的比较见图5与图6。
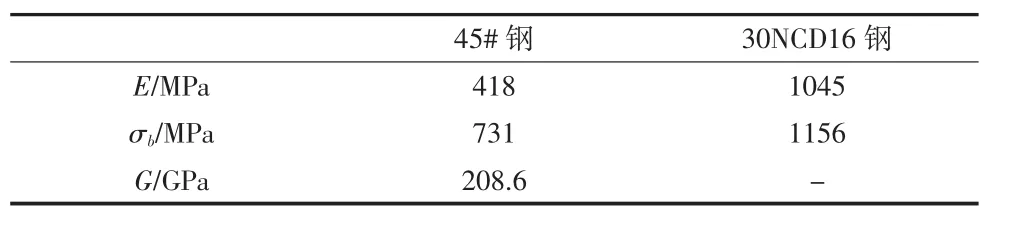
表1 材料的力学性能参数

表2 疲劳寿命预测模型的相关材料常数

图5 SM45C钢预测寿命与试验寿命比较

图6 30NCD6钢预测寿命与试验寿命比较
本文模型适用于单轴、多轴比例、非比例等各种加载情况,且误差分散带在2个因子以内,预测寿命与试验寿命吻合较好。
4 结论
(1)提出了一种新的剪应力等效幅值的计算方法。利用应力不变量求解剪应力等效幅值时,需要对疲劳损伤估算进行充分考虑,并建立与之相应的参考坐标系,并且还需要记利用空间向量范数。
(2)提出了一种基于应力不变量的处理多轴高周复杂载荷的多轴疲劳寿命估算模型。经过试验数据验证,寿命预测结果与试验结果吻合较好。
