多喷嘴无扩压室引射器性能计算的研究
2019-06-21刘剑飞袁庆燕
刘剑飞,袁庆燕
(1.空装驻新乡地区军事代表室;2.新乡航空工业(集团)有限公司,河南 新乡453049)
0 引言
直升机环控系统在地面停机状态或低速飞行状态下工作条件非常恶劣,为此在环控系统制冷组件的散热器冷风道上加装引射器,以保证散热器冷边流量,改善环控系统的工作条件。多喷嘴引射器由于具有混合室长度短,流场分布均匀,重量轻等优点,被越来越多地应用到直升机上。
Zeune和Runkin[1]运用动量平衡方程建立了引射器的基本理论基础;Keenan和Neulnann[2]建立了一维等压混合模型,该模型是现在引射器理论分析的主要计算模型;Stoecker[3]认为引射流体经接受室收缩段加速后达到声速,然后工作流体和引射流体以临界压力进行混合;Kim[4,5]等人用CFD软件模拟分析了引射器喉管面积对引射性能的影响。
王锁芳、李立国[6]对六喷嘴超音速进行性能计算和试验验证,结果表明随着工作流体的压力比引射流体(PP/PH)的增加,引射比和引射比修整系数下降;邱义芬[7]等人提出了多喷嘴引射器的计算方法,并经试验验证,结果表明该方法精度较高;廖达雄[8]等人采用一维的处理方法,分析了各参数对引射性能的影响;何培杰[9]等人采用大涡模型对引射器的内部流动进行二维仿真计算,结果表明该方法可以较好的模拟引射器内部流动。
这些研究均偏重于标准结构的引射器研究,即该类引射器有喷嘴、接受室、混合室和扩压室完整的结构,而对无扩压室的引射器研究较少,由于航空领域对重量指标要求较高,无扩压室引射器运用更为广泛。因此,本文对多喷嘴无扩压室引射器性能进行理论分析,为该类引射器工程设计提供理论依据。
1 工作原理简介
从发动机引来的高温高压气体通过引射器喷嘴的膨胀作用形成一股射流,这股射流暴露在冷风道的低能量流中并且在高、低能量两股流体之间形成一个剪切面,通过粘性剪切力和流体扩散的机械作用,高速工作流体的动量和动能逐渐传递给吸入的引射流体,当混合完成后,工作流体和引射流体将成为能量和速度分布相同的一股流体,从而达到引射的目的。工作介质流叫做工作流体。工作流体以很高的速度从喷嘴出来,进入喷射器的接受室,并把在喷射器前的压力较低的介质吸走,被吸走的流体叫做引射流体。
引射器的工作原理是基于以下三个基本物理定律。
(1)能量守恒定律
ip+ μiH=(1+ μ)ic
式中:ip为在滑油散热引射器前工作流体的焓,kJ/kg;
iH为在滑油散热引射器前引射流体的焓,kJ/kg;ic为在滑油散热引射器之后混合流体的焓,kJ/kg;
(2)质量守恒定律
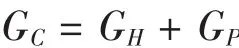
式中:GP为工作流体的质量流量,kg/s;
GH为引射流体的质量流量,kg/s;
GC为混合流体的质量流量,kg/s。
(3)动量守恒定律

式中:ωP1为在混合室入口截面上工作流体的速度(m/s);
ωH1为在混合室入口截面上引射流体的速度(m/s);
ωC为在混合室出口截面上混合流体的速度(m/s);
PP1为在混合室入口截面上工作流体的静压力(Pa);
PH1为在混合室入口截面上引射流体的静压力(Pa);
PC为在混合室出口截面上混合流体的静压力(Pa);
fP1为进入混合室时工作流体的截面面积(m2);
fH1为进入混合室时引射流体的截面面积(m2);
fC为在混合室出口处混合流体的截面面积(m2);
2 引射器性能分析
2.1 理论计算
(1)计算相对压力
相对压力:指在给定截面上等熵流动气体静压力与滞止压力之比。

式中,PH为引射流体压力,Pa;
PP为工作流体压力,Pa。
(2)根据 ΠPH和气体动力函数表得到:λPH,qPH,εPH。
其中,λPH为折算等熵速度;
qPH为折算质量速度;
εPH为相对密度。
(3)计算混合流体出口温度
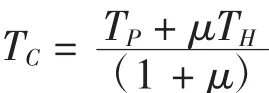
式中,TC为混合流体温度,K;
TP为工作流体温度,K;
TH为引射流体温度,K。
(4)计算相对比体积
因为压力pc事先不知道,预先取pc=pH。可以得到:

(5)计算最佳截面比(fc/fp*)最佳
在计算过程中,速度系数值选定为:φ1=0.95;φ2=0.975;φ3=0.9;φ4=0.925

式中,a= φ1φ2qPH;

(6)计算特性曲线方程

式中,fH2=fc-fp1
本文以给XX型飞机配套的滑油散热引射器为例,进行性能分析。
试验件的物理结构为:引射流体入口面积为480 mm×240 mm;混合流体入口面积为260 mm×200 mm;喷嘴的喉部直径d1为3.6 mm,出口直径为5 mm,喷嘴共有20个,均匀分布在200 mm×100 mm的长方形边线上;喷嘴出口距混合室入口的长度为250 mm,混合室长度为300 mm。计算结果如表1所示。

表1 理论计算引射比(μ1)
2.2 仿真计算
本文使用Ansys17.2软件,采用标准的k-ε双方程模型,运用雷诺时均方程法对模型进行仿真计算。
2.2.1 仿真计算模型
在ANSYS-Workbench中导入引射器的三维模型,对其进行合理简化,最终得到的仿真计算模型如图2所示。
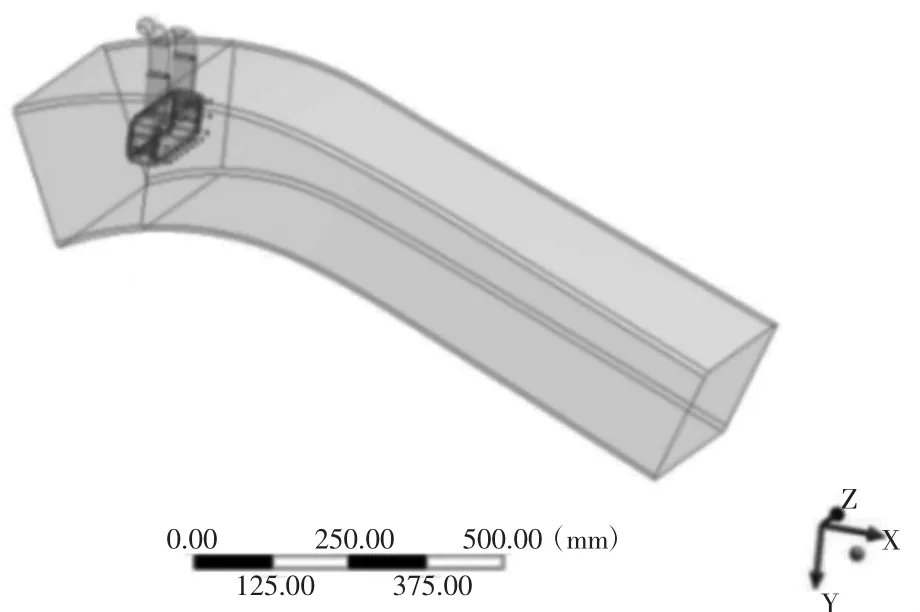
图2 流体简化模型
2.2.2 计算流体域网格划分
本文采用了四面体单元对其进行网格划分,经网格无关性验证分析,最终网格单元数量1000万。
2.2.3 边界条件的确定
从引射器结构图,可以得出共有5个边界:工作流体入口、引射流体入口、引射器壁面、对称轴和混合室出口。
(1)工作流体入口边界条件
工作流体入口边界条件设为速度入口,速度大小由工作流体的温度来确定。
(2)引射流体入口边界条件
引射流体入口边界条件取压力入口边界,引射流体入口压力为一个大气压,即101 kPa(绝压),温度为25℃。
(3)引射器内壁面处理
本模型取固壁边界,即零速度边界条件,同时认为引射器与外界无热交换。
(4)中心对称轴边界条件
中心对称轴取物理模型的对称轴。
(5)混合室出口边界条件
混合室出口边界取压力出口边界,本模型认为混合流体的出口压力为大气压,即101 kPa(绝压)。
2.2.4 仿真结果分析
为清楚的反应引射器内部的流场分布情况,本文截取沿流动方向的截面。
(1)速度场分布(如图 3)

图3 速度流场分布图
(2)流线图(如下图)


图4 流线图
(3)组分分布云图(如图5)
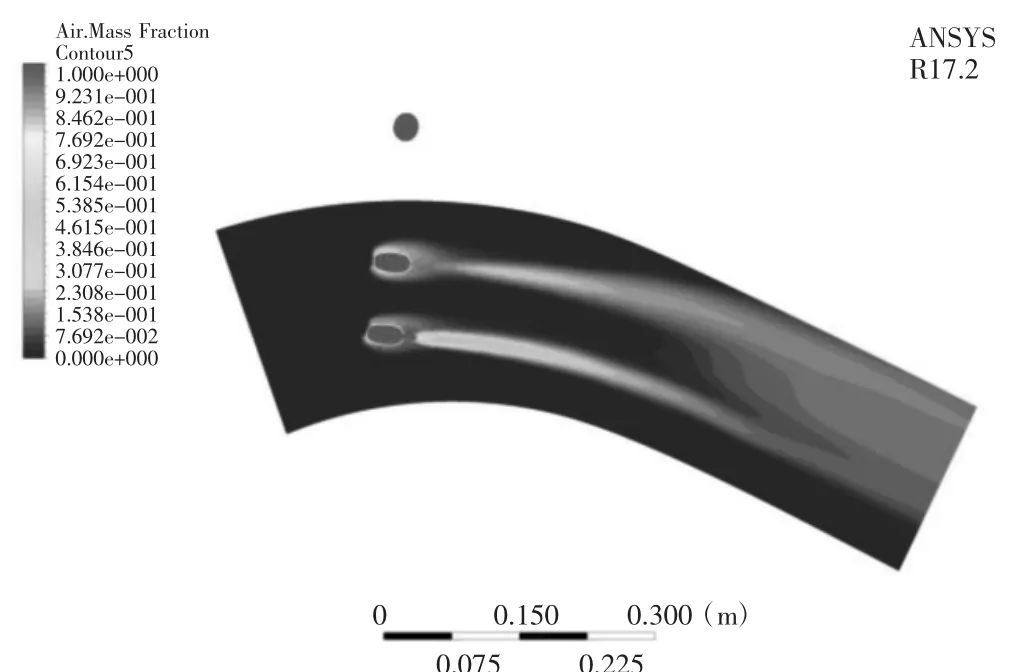
图5 组云布云图
经仿真分析可知,引射器在工作压力0.48 MPa(绝压)、温度265℃,入口流量为756 kg/h,被引射的冷边入口质量流量为9 637.2 kg/h,引射比为12.7。试验值为12.14,理论计算与试验值较为接近。由于计算量较大,本文仅对一个点进行仿真计算,导致结果存在一定的偶然性。
2.3 试验分析
2.3.1 试验装置
试验装置主要由试验件、工作流体管路、混合流体管路和测量温度、压力流量仪表等组成。试验的测试系统如图6所示。

图6 试验的测试系统
2.3.2 试验结果和分析
试验结果如表2所示。
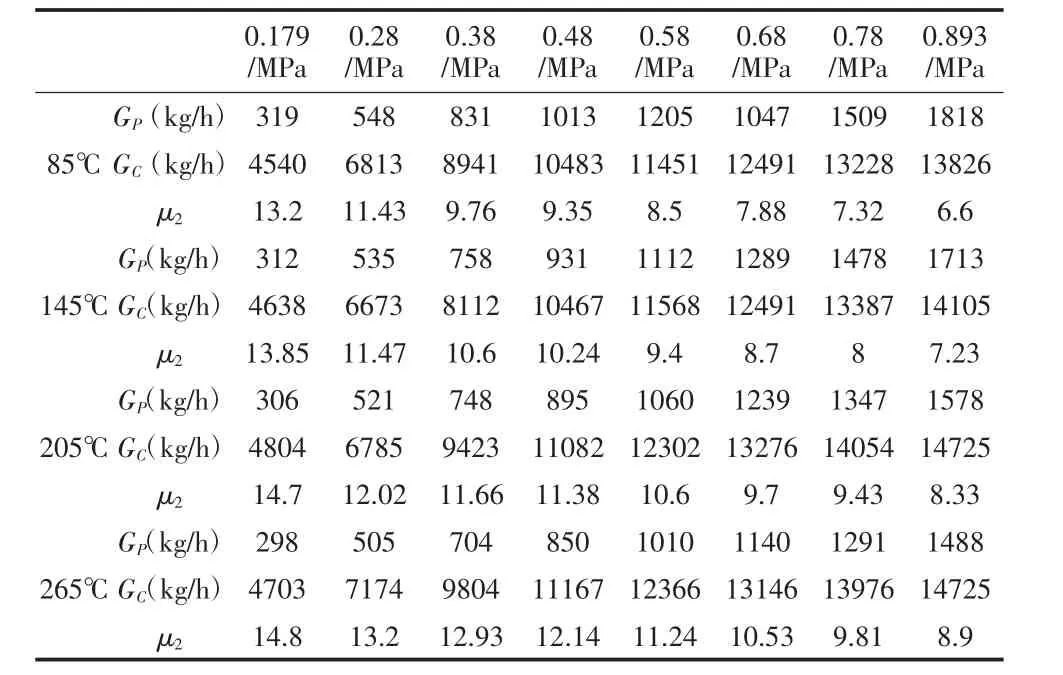
表2 试验数据
定义一个新的函数来评价理论计算的误差率。

式中,μ1为理论计算的引射比;μ2为试验测出的引射比。
计算结果如表3所示。误差率变化曲线如图7所示。
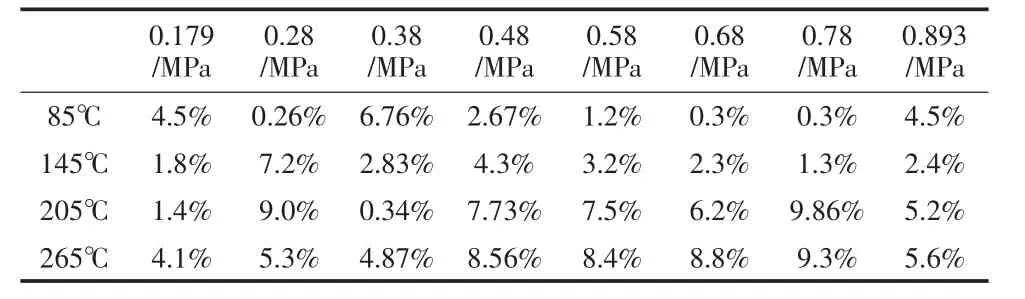
表3 误差表

图7 误差率
通过上述分析,理论计算的误差率小于10%,计算精确度较高,可以满足工程设计需求。
3 结论
通过以上的理论分析和试验对比可以得出以下结论:
(1)本文中给出的引射比计算方法误差小于10%,说明本文给出的计算方法是准确可靠的,可以满足工程设计需求。
(2)工作流体的温度和压力对理论计算的精度影响较小。
