基于PSO的永磁同步电机SMC控制研究

张庆宇，涂群章，蒋成明，黄 皓，张 帅

（中国人民解放军陆军工程大学野战工程学院，江苏 南京210007）

0 引言

永磁同步电机（PMSM）因其结构简单、功率密度高等优点被广泛应用于电动车辆传动系统中，模型为多变量、强耦合的非线性时变系统[1]，采用常规的PID控制不能满足PMSM高性能控制需求[2]。

国内外学者根据永磁同步电机控制系统的特性提出了矢量控制[3]、模糊控制[4]、神经网络控制[5]、弱磁控制[6]、滑模变结构控制[7]（SMC）等控制策略。

其中SMC因其抗干扰、实现简单等优点被广泛应用于PMSM控制。文献[8]在传统SMC控制策略的基础上，提出基于NTSM的模糊控制策略，有效提高了电机动态与稳态性能，增强了电机抗干扰能力。文献[9]提出一种积分型SMC控制策略有效提高电机控制精度。

以上控制策略有效提高了电机控制性能，但无法在有效时间内及时反馈电机输出，为了提高永磁同步电机调速系统的动态品质，在建立指数趋近律控制变结构控制[10]基础上采用粒子群算法（PSO）对SMC的参数进行优化。建立控制系统起动与突增负载的仿真与实验模型，结果表明，该控制系统有效提高了系统控制精度、鲁棒性。

1 永磁同步电机数学模型

为优化永磁同步电机控制算法，需要建立合适的PMSM数学模型。以表贴式永磁同步电机为分析对象，假定三相PMSM为理想电机。建立同步旋转坐标系d-q下的数学模型，其定子电压为：

其中，ud，uq为d-q坐标系下定子电压的d-q轴分量，id，iq为d-q坐标系下定子电流的d-q轴分量，ψd，ψq为 d-q 坐标系下定子磁链的 d-q 轴分量，Ld，Lq为d-q轴电感分量，ωe为电角速度，R为定子的电阻，ψf为转子磁场等效磁链。

此时电磁转矩方程可写为：

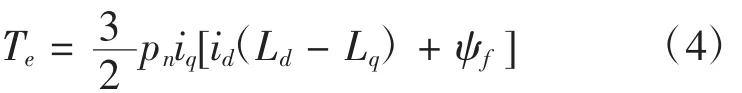
Te为永磁同步电机转矩，pn为电机极对数。

2 PMSM的SMC控制

滑模控制与传统的PID控制区别在于控制的不连续性，使系统结构随时间变化。这种滑动模态变结构控制具有快速响应、对参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单[11]等优点。为使正常运动阶段满足滑动模态的可达性条件ss.＜0，选用指数趋近律确保趋近运动品质[12-14]。

定义系统的滑模面函数为：

对滑模面函数求导为：

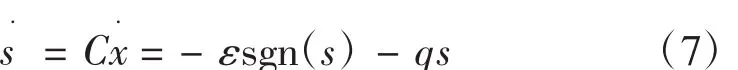
可以求取控制器u为：

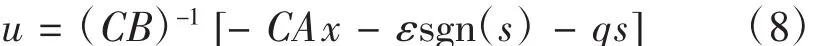
建立d-q坐标系下的PMSM的SMC控制模型

其中Ls为定子电感。

采用id=0的转子磁场定向控制方法对表贴式PMSM进行控制，可以获得良好效果。

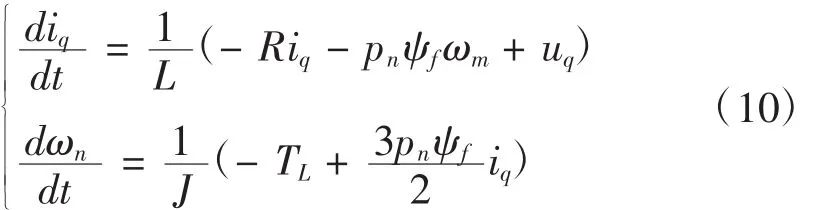
定义PMSM系统状态变量：

其中，ωref为电机参考转速，通常为常量。ωm为实际转速，对上式微分，得：

则式可为：

定义滑模面函数为：

其中，c为待设计参数。对式求导得：

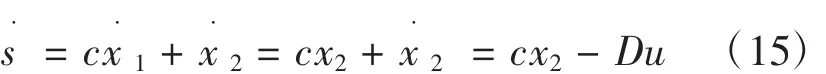
联立公式（5）、（15）可得控制器的表达式为：

从而得到q轴参考电流为：

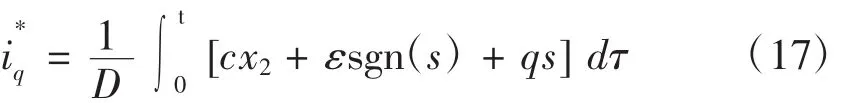
控制器包含积分项，可以削弱抖振现象，提高系统控制品质。

3 基于粒子群算法的SMC控制优化

粒子群算法速度、位置更新公式为：

其中，x表示粒子的位置，v表示粒子的速度，w为惯性因子，k1、k2为加速常数，r1r2为[0，1]之间的随机数，pt是粒子迄今为止搜索到的最优位置，Gt是整个粒子群迄今为止搜索到的最优位置。

基于PSO的SMC控制流程[15]如图1所示：

图1 基于PSO的SMC控制流程图

PSO产生粒子群后，将该粒子群中的粒子依次赋给SMC控制器的参数c、ε、q，然后运行控制控制系统Simulink模型不断更新粒子群在控制系统中的速度、得到该组参数对应的性能指标，选用ITAE作为误差评价指标，其定义为：

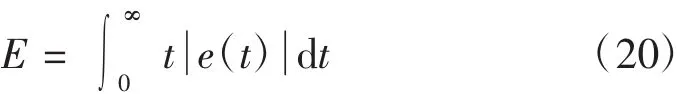
选取被控对象为SMC控制下的PMSM，其工作原理如图2所示。

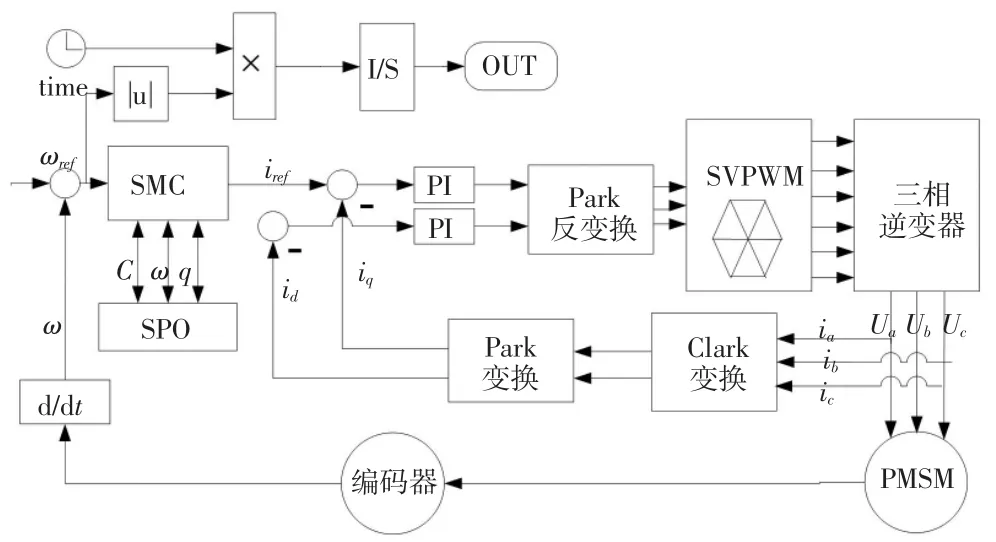
图2 PMSM的PSO-SMC控制系统

4 仿真分析与实验研究

利用Matlab工具箱建立Simulink模型对其进行仿真分析，并在TI公司的TMS320F28035为控制芯片的开发套件上搭建实物系统。PMSM参数为：极对数pn=4，定子电感Ls=8.5 mH，定子电阻R=2.975 Ω，磁链 Ψf=0.175 Wb，动惯量 J=0.003 kg·m2，逆变器开关频率为10 kHz。

图3、图4、图5为系统起动和突增负载的动态响应仿真结果。电机转速1 000 r/min，系统起动在0.2 s时负载转矩从0突增至10 N·m，图3表示了两种控制策略下转速、转矩、三相电流的动态响应仿真结果。

图3 两种控制策略下的PMSM转速响应仿真曲线

图4 为系统起动和突增负载的动态响应实验结果。系统起动在0.2 s时负载转矩从0突增至10 N·m，图4表示了两种控制策略下转速、转矩的动态响应仿真结果。

图4 两种控制策略下的PMSM转矩响应仿真曲线

从图3、图4可以看出，基于PSO的SMC控制器在响应超调量、调整时间、系统稳定性、抗外界扰动能力上均优于传统SMC控制器。

图3表示了基于传统SMC控制与PSO-SMC控制的转速动态响应仿真结果。仿真结果表明，传统SMC控制下的转速响应上升时间tr为0.0108 s，超调量Mp为52.1%；PSO-SMC控制下的转速响应上升时间为0.0102 s，超调量为28.7%.在PSO-SMC控制下转速响应时间降低了约5.6%，超调量降低了约44.9%。在空载运行时间段内，初始时电机在两种控制策略下稍有波动，PSO-SMC控制下的转速波动较小。

图4、图5表示了基于传统SMC控制与PSOSMC控制的转矩、电流动态响应仿真结果。在初始启动与变负载阶段，PSO-SMC控制下的转矩、电流动态响应波动较传统SMC控制较小。

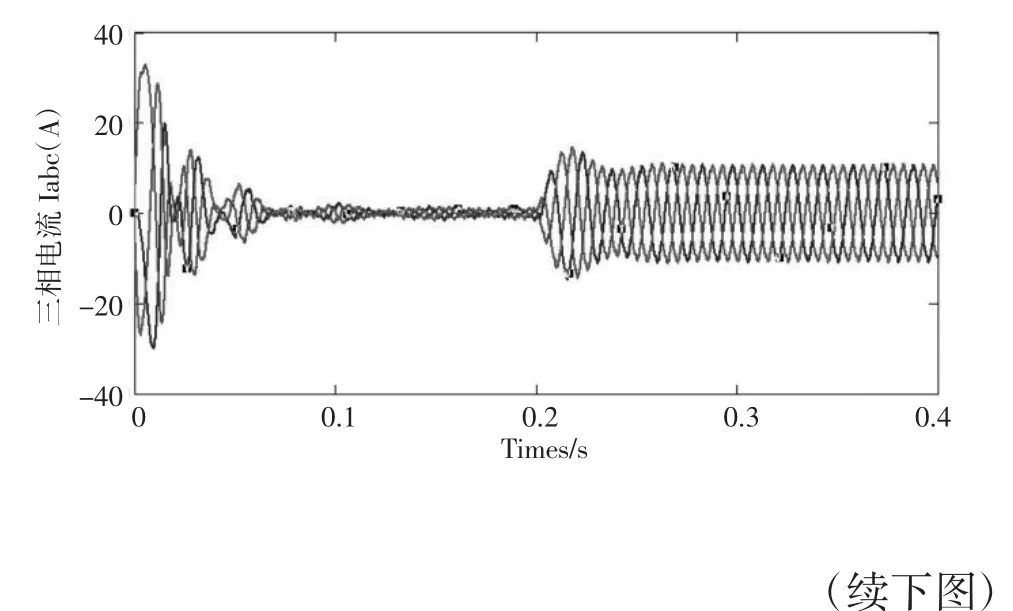
图5 两种控制策略下的PMSM电流响应仿真曲线

图6 、图7为系统起动和突增负载的动态响应实验结果。电机转速1 000 r/min，系统起动在0.2 s时负载转矩从0突增至10 N·m。

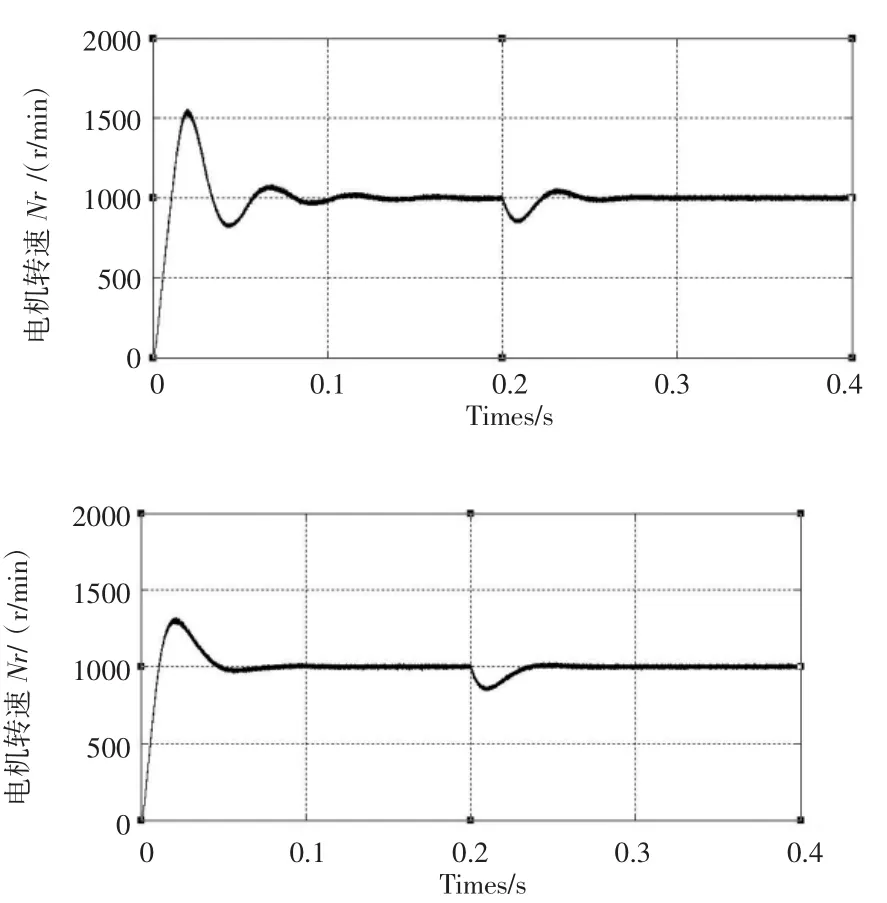
图6 两种控制策略下的PMSM转速响应实验曲线

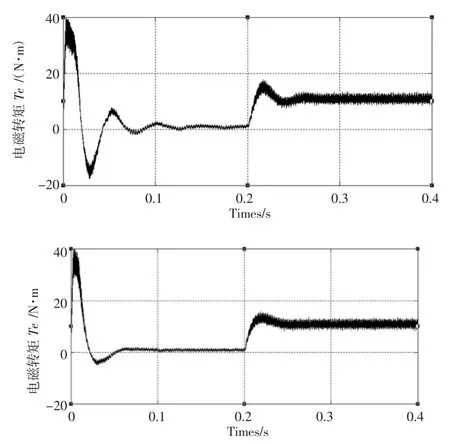
图7 两种控制策略下的PMSM转矩响应实验曲线

由图6、图7可知，基于PSO的SMC控制器在响应超调量、系统稳定性、抗外界扰动能力上均优于传统SMC控制器。

5 总结

针对永磁同步电机控制策略的不足，本文设计一种基于PSO-SMC算法优化的PMSM控制器。首先建立理想永磁同步电机在旋转坐标系d-q下的数学模型，然后建立采用指数趋近律的SMC速度控制模型，采用粒子群算法对SMC控制器参数c、ε、q进行优化，最后采用仿真实验对其性能进行测试。实验表明，该控制方法较传统的SMC控制调制性能更优，响应的超调量和调整时间明显减小，动态和稳态性能明显改善。