滚齿机传动链误差测量误差分析及辨识

龙 谭 ，王时龙 ，任 磊 ，杨 勇

（1.重庆大学，机械传动国家重点实验室，重庆 400044；2.重庆机床集团有限责任公司，重庆400055）

0 引言

滚齿加工是一种生产效率高、应用广的齿形加工方法[1]。滚刀轴、电子齿轮箱和工作台构成滚齿机传动链，是滚齿机的关键核心部件。滚齿机传动链误差不仅会引起工件齿轮的螺距误差、齿廓误差和工件螺旋误差，还会诱导滚齿机的振动和噪声[2]。准确测量传动链误差，对通过传动链误差准确分析机床传动链性能以及传动链误差精确补偿具有十分重要的意义。

基于编码器和圆光栅广泛用于滚齿机床传动链误差的测量[3-6]，离散角度采样的方法适合于使用编码器测量旋转机械中多路信号的情况[7]；Palermo等人[8]讨论了使用低成本数字编码器来测量高速传动系统的方法；Zhou等人[9]和Zhao等人[10-11]利用机床内置编码器采集机床传动链的传动误差信号，用于确定传动链中的故障源；Brecher等人[12]测量齿轮组传动误差和噪声情况以研究齿轮组的传动误差与齿轮箱在其应用中的噪声特性之间的相关性；彭等人[13]和李等人[14]利用FMT系统对滚齿机进行传动误差测量，并通过修正传动齿轮。通过传动链误差准确分析机床传动链性能以及传动链误差精确补偿的前提为传动链误差的精确测量。

为保证测量的精确性，Du等人[15]研究了包含齿轮的驱动系统的编码器测量误差，并提出一种减少编码器误差的方法；Li等[16]基于阿贝原则分析了转台倾斜运动误差和径向运动误差引起的圆光栅角位移测量误差及其对转台定位精度的影响规律；Lopez等人[17]分析了振动对和读数头的摆动引起的编码器测量误差，并基于对恶化的测量信号的利萨如图的拟合技术提高传感器精度。除上述方法外，雷尼绍海德汉等厂商推出了多读数头的圆光栅以消除测量误差，但成本高昂且安装不便。针对基于单读数头圆光栅的传动链误差测量系统的测量误差分析及消除技术亟待研究。

本文考虑圆光栅的制造误差和装配误差，分析传动链误差测量平台的测量误差；基于测量误差相位特性提出了一种新的修正测量系统误差的方法，通过两次不同安装位置下的测量数据计算并消除测量误差；基于YDA1132型滚齿机的实验表明该方法能准确计算并消除测量误差，同时流程简单成本低。

1 测量误差分析及辨识原理

1.1 传动链误差测量方案

滚齿机传动链包括滚刀轴电机、滚刀箱、电子齿轮箱、工作台电机以及工作台传动装置。传动链误差即为由传动副传动误差和伺服控制误差引起的工作台和滚刀轴间的相对运动误差，如式（1）所示。

式中，eT为传动链误差；φC为工作台转角；φB为滚刀轴转角；α为工作台与滚刀转速比。

如图1所示，工作台与滚刀轴末端分别安装高精度圆光栅，同步采集滚刀轴和工作台的角位置，计算传动链误差。主要设备详细参数如表1所示。

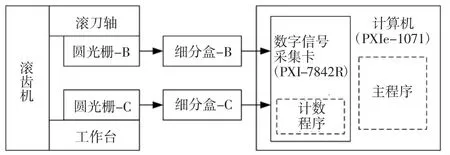
图1 传动链误差测量平台

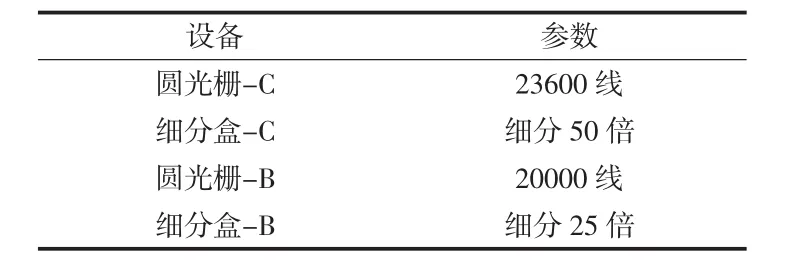
表1 主要实验设备参数表

为明确传动链误差沿工作台的空间分布情况，首先测量圆光栅参考点相对机床工作台原点的相位差，并从第一次检测到圆光栅的参考点开始进入计数程序；计数程序以圆光栅-C产生的TTL信号的下降沿为触发信号，将2路编码信号的计数值写入FIFO结构，主程序读取FIFO中的计数值计算再该点处的传动链误差。

1.2 测量误差分析

圆光栅的刻线在制造过程中无法保证完全均匀，且在安装过程中刻线与读数头之间存在相对位姿误差。因此，圆光栅测量角位移时存在与读数头位置相关的测量误差误差。圆光栅误差对传动误差的作用为：

式中△为圆光栅测量误差对传动链误差测量值的贡献量；i为圆光栅与工作台转速比；em为圆光栅误差。

滚刀轴的圆光栅与工作台转速比通常较高，而工作台的圆光栅与工作台转速比为1。因此，传动链误差测量系统的误差主要由工作台编码器引起，而滚刀轴的圆光栅的误差的影响可忽略不计。

刻线沿圆光栅钢毂周向分布，读数头检测扫过的刻线。如图2所示，过渡盘与工作台固联，钢毂托架与过渡盘通过锥面连接，圆光栅钢毂与钢毂托架通过锥面连接，读数头与机架固联。为保证圆光栅安装精度，安装时取过渡盘的锥面在P和Q截面的跳动尽量小。此时，可近似认为圆光栅的位姿误差取决于两组锥面配合的误差。

图2 工作台圆光栅安装示意图

如图 3（a）和图 3（b）所示，圆光栅旋转到该位置时，理想状态下读数头检测到M处的刻线；位姿误差导致读数头检测到M′处的刻线。安装导致的测量误差为二者之间的绕Z轴的偏转误差。误差量相对圆光栅尺寸很小，因此绕Z轴的偏转误差近似为：

其中位姿误差中X方向的偏差和绕Y轴最易引起绕Z轴的偏转误差，由图3（b）有

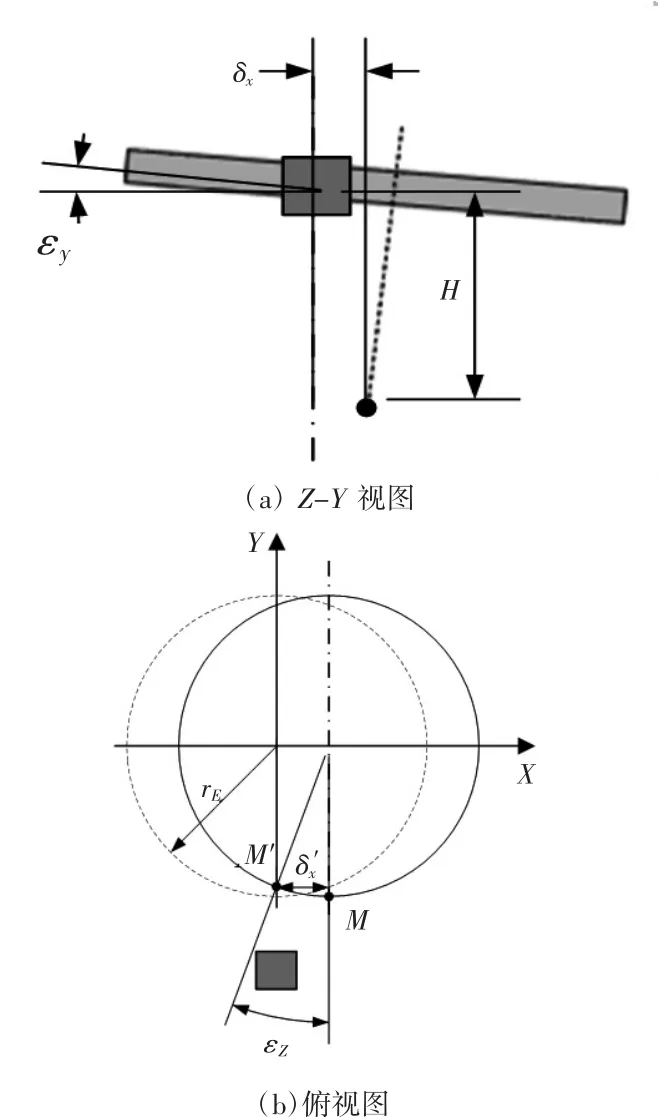
图3 工作台圆光栅安装误差

圆光栅相对过渡盘的位姿误差是固定的，圆光栅随工作台旋转时，圆光栅钢毂相对读数头的位姿误差周期性地变化，如式。因此，圆光栅安装误差导致的测量误差将沿工作台的一周分布，且主要为1次谐波，如式：

保证过渡盘不动，若钢毂托架和读数头转动相同角度β，则有

刻线沿圆光栅钢毂周向分布，因此刻线制造误差对测量误差的贡献值的周期与圆光栅钢毂旋转周期一致。若读数头相对工作台转动β，则圆光栅的参考点相对机床工作台发生β相位移动，且前后两次测量中刻线误差导致的测量误差的关系为：

式中，ξ为第一次测量中刻线误差导致的测量误差；ξ′为第二次测量中刻线误差导致的测量误差。

测量误差为工作台圆光栅的制造误差和安装误差综合表现，即：

式中，ψ为测量误差。

综上所述，机床传动链误差决定于机床几何结构和机床轴转速；测量误差决定于圆光栅钢毂的安装误差和光栅刻线的制造误差，且主要包含1次谐波。因此，改变读数头和圆光栅钢毂托架，传动链误差没有发生变化，但测量误差相对工作台发生相位改变，则

1.3 测量误差辨识方法

如图4所示，机床工作台参考原点为M；第一次测量的圆光栅读数头的位置为E1，与工作台原点间隔α1；第二次测量的圆光栅读数头位置为E2，与工作台原点间隔α2。第一次和第二次传动链误差的测量值，如式：

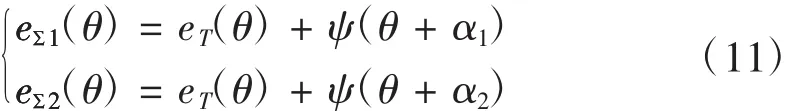
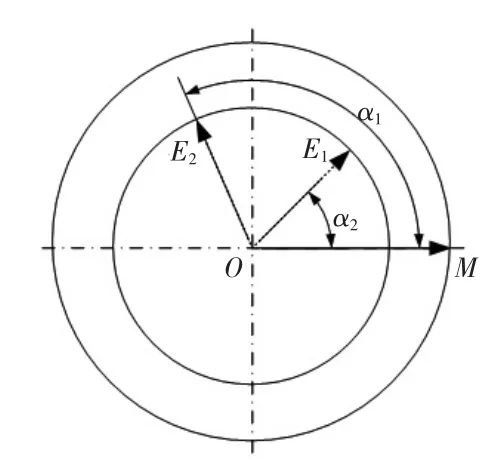
图4 两次测量的参考点位置

滚齿机传动链误差包括多级传动副的传动误差和滚刀轴、工作台编码器的测量误差，可表示为

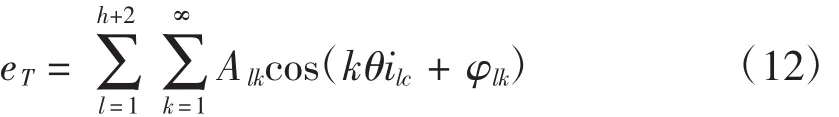
式中，Alk为l齿轮（或编码器）的k次谐波的幅值；φlk为l齿轮（或编码器）的k次谐波的初相位；ilc为l齿轮（或编码器）与工作台的转速比。

由式（12）可知，滚齿机床传动链误差中存在多种谐波。同时，圆光栅的测量误差对传动链误差中2次以上谐波影响很小。为避免随机误差等的影响，提高测量误差的计算精度，采用DFT和IDFT对传动链误差测量数据滤波，仅保留1次谐波，式（5）为1次谐波的复数域表达。

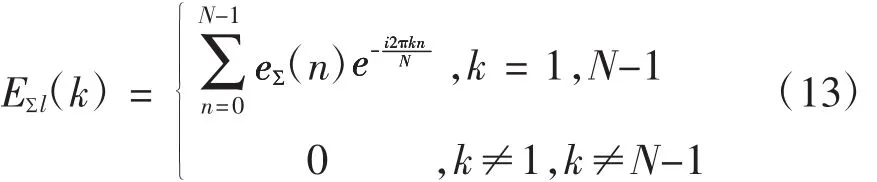
第一次和第二次传动误差测量值的差值1阶谐波的复数域表达为

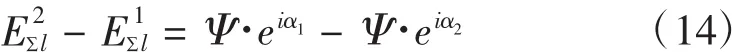
式中Ψ为测量误差复数域表达。

即有测量误差为

进而由离散傅里叶逆变换得到测量误差，则传动链误差的真实值为：

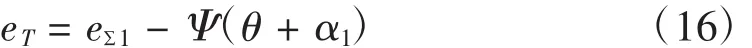
2 实验

2.1 实验原理

如图5所示，实验分为两部分，其一为两次测量工作台定位误差，以激光干涉仪测定的数据为准，圆光栅-C的测量误差即为两次定位误差的差值，作为参照组；其二为两次测量机床传动链误差，通过本文方法计算测量误差，与参照组所得测量误差形成对比。

图5 实验原理图

实验对象为YDA3132型滚齿机，在测量传动链误差时，为形成对照，设定滚刀轴转速为50 r/min，滚刀头数为2，工件齿数为44，则滚刀轴与工作台转速比为44∶2。此时工作台转速为0.83 r/min，因此认为圆光栅-C测量定位误差时的测量误差和测量传动链误差时的测量误差是一致的。

2.2 实验流程

1）安装滚刀轴圆光栅和工作台圆光栅，安装时，工作台过渡盘的锥面选择两个水平面，缓慢转动工作台，控制这两个截面上跳动小于1μm；

2）激光干涉仪测量机床工作台定位误差；

3）测量圆光栅-C参考点与机床工作台原点的相位差，第一次测量传动链误差；

4）工作台圆光栅测量机床工作台定位误差；

5）保持过渡盘不动，旋转钢毂托架和读数头，旋转角度接近180°；

6）测量圆光栅-C参考点与机床工作台原点的相位差，第二次测量传动链误差。

3 结果与分析

如图6（a）所示，滚齿机床传动链误差的第一次测量结果和第二次测量结果对比，其大周期误差明显存在相位差，即滚齿机传动链误差测量值含有测量平台的测量误差，且测量误差明显影响了传动链误差测量的准确性。

如图6（b）所示，第一次和第二次传动链误差测量值的离散傅里叶变换的1阶分量幅值分别为13 arcsec和10 arcsec，二者存在明显差异，但2阶以上分量基本重合，其中包括与滚刀轴相关的频率为22的谱线。结果印证了传动链误差检测平台中来自于工作台圆光栅的测量误差主要为1次谐波误差，滚刀轴圆光栅的测量误差对传动链误差的影响很小。因此，对传动链误差测量数据采用傅里叶变换和傅里叶逆变换滤出1阶谐波，再计算测量误差能够表征大部分的测量误差且能减小数据中随机成分对计算的影响。

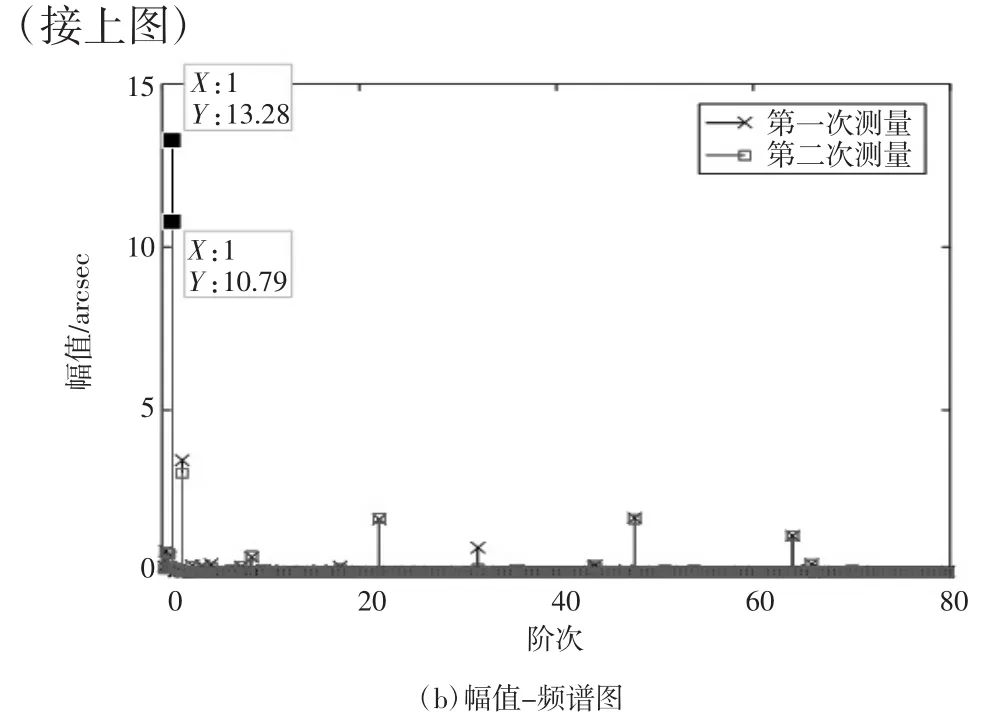
图6 滚齿机传动链误差两次测量值

如图7所示，圆光栅-C测定的工作台定位误差相比于激光干涉仪测定的工作台定位误差，波峰出现的位置更靠后、峰峰值更小。即该实验中测量误差使工作台定位误差测量值比工作台定位误差真实值更大，且发生了一定的相位移动，与分析结果相符合。

图7 两次工作台定位误差结果

如图8所示，菱形标记实线为圆光栅-C测定的工作台定位误差与激光干涉仪测定的工作台定位误差的差值，虚线为其1阶谐波拟合曲线，其拟合曲线幅值为5.8 arcsec，相位为2.72；无标记实线为由两次传动链误差测量值计算得到的圆光栅-C的测量误差，幅值为5.5 arcsec，相位为2.71。在1阶频率上，测量误差修正方法计算所得测量误差与两次定位误差比较所得测量误差，差值仅为0.3 arcsec，同时受工作台的重复定位精度影响，两次定位误差的差值在2阶以上还存在小幅波动。

图8 两组测量误差对比

鉴于激光干涉仪的测量精度较高（回转轴定位测量的分辨率为0.01 arcsec），因此以激光干涉仪的测量数据为准，两次定位误差的差值作为圆光栅-C的测量误差的标准。因此通过对比两组实验所得的测量误差，证明本文提出的测量误差辨识方法能够有效辨识出传动链误差测试平台的测量误差。

根据辨识得到的测量误差分别对两次测量数据进行修正，得到图9所示第一次传动链误差测量值、第二次传动链误差测量值的修正后的曲线。二者的大周期误差整体趋势一致，印证了修正方法的有效性。

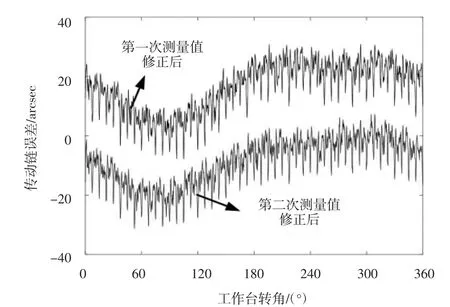
图9 修正后的滚齿机传动链误差测量值

5 结束语

本文分析了圆光栅的制造误差和装配误差对传动链误差测量系统的测量误差的影响，结果表明，测量误差主要为1次谐波；两次不同安装位置下，测量误差的相位差与两次不同安装位置的相位差相同。

基于测量误差的相位特性提出了一种新的修正系统测量误差的方法，在实验中根据两次不同安装位置下的测量数据和圆光栅与工作台的相位差辨识出了机床传动链测量平台的测量误差，提高了检测平台的测量精度。该方法步骤简单，成本低廉，非常适合在生产现场进行应用。