基于MATLAB编程的刚体转动惯量实验数据处理方法探讨*

李 立 张皓晶 张 雄

(云南师范大学物理与电子信息学院 云南 昆明 650500)

1 引言

物理是一门以实验为基础的学科，开设大学物理实验课程，其目的不仅让学生理解整个物理实验过程，还要培养和提高学生对实验的操作能力.中外学者在近期的研究中提出:“教师要充分利用现代教育技术辅助教学，大力开发并向学生提供更为丰富的学习资源，把现代信息技术作为学生学习物理和解决问题的有力工具，致力于改变学生的学习方式，使学生乐意并有更多的精力投入到现实的、探索性的物理活动中去”[1,2].而且，教育信息化能共享教育资源，对于发达城市学校和边疆少数民族学校的学生，也是一种公平的受教育条件[3].

在理工科大学的物理实验中,测量刚体转动惯量的方法有很多，例如转动法、三线摆法、扭摆法、复摆法等[4]，本文所采取的测量方法是转动法，结合MATLAB App Designer可视化对实验数据进行处理，一方面可以使学生从复杂的数据处理中解放出来，另一方面也可以加深学生对于实验的体会和思考,提高实验教学的有效性.

2 实验原理

根据刚体转动定律，当刚体绕固定轴转动时，有[4]

M=Iβ

(1)

其中M为刚体所受合力矩，I为物体对该轴的转动惯量，β为角加速度.刚体所受外力矩为绳子给予的力矩Tr和摩擦力矩Mμ，其中T为绳子张力，r为塔轮的绕线半径.当略去滑轮及绳子质量并认为绳长不变时，m以匀加速度a下落,有[4]

T=m(g-a)

(2)

其中g为重力加速度，质量为m的砝码由静止开始下落高度h所用时间为t，则

(3)

又因为

a=rβ

(4)

所以

(5)

在实验过程中保持g≫a， 则有

(6)

(1)保持r，h以及m0的位置不变，改变m，测出相应的下落时间t，并保持Mμ不变，有

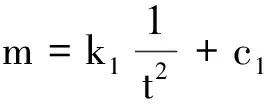
(7)

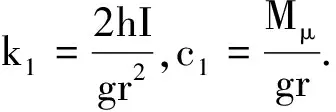
(2)保持h，m以及m0的位置不变，改变r，测出相应的下落时间t，并保持Mμ不变,有

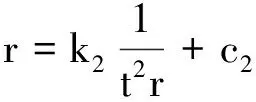
(8)

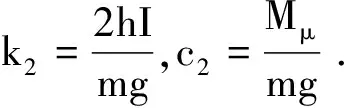
3 实验方法

(1)调节实验装置.

(2)选取r=2.50 cm,将m0置放于(5, 5′)，将m从固定高度h静止下落，通过增加砝码改变质量m，直到m=35.00 g为止，用停表测下落时间t.

(3)将m0置放于(5, 5′)，维持m=20.00 g，将m从固定高度h静止下落，通过改变绕线半径r，取r=1.00， 1.50，…，3.00 cm，用停表测下落时间t.

(4)维持m=20.00 g，r=2.50 cm，对称地改变m0的位置，令其与转轴相距x1，x2，…，x5，记录下落时间t，作出x2-t2图像，检验平行轴定理.

4 软件的界面和实验数据处理示例

4.1 软件的界面

MATLAB图形用户界面是指用户与计算机程序的接触点或交互方式,是用户与计算机进行信息交流的界面[5].本文使用MATLAB App Designer可视化编程进行实验数据及图像的处理，软件的界面如图1所示，界面上包括下降距离、半径、质量和m0位置输入框、实验数据输入表、实验数据处理结果、数据初始化、数据处理和图像绘制按钮.

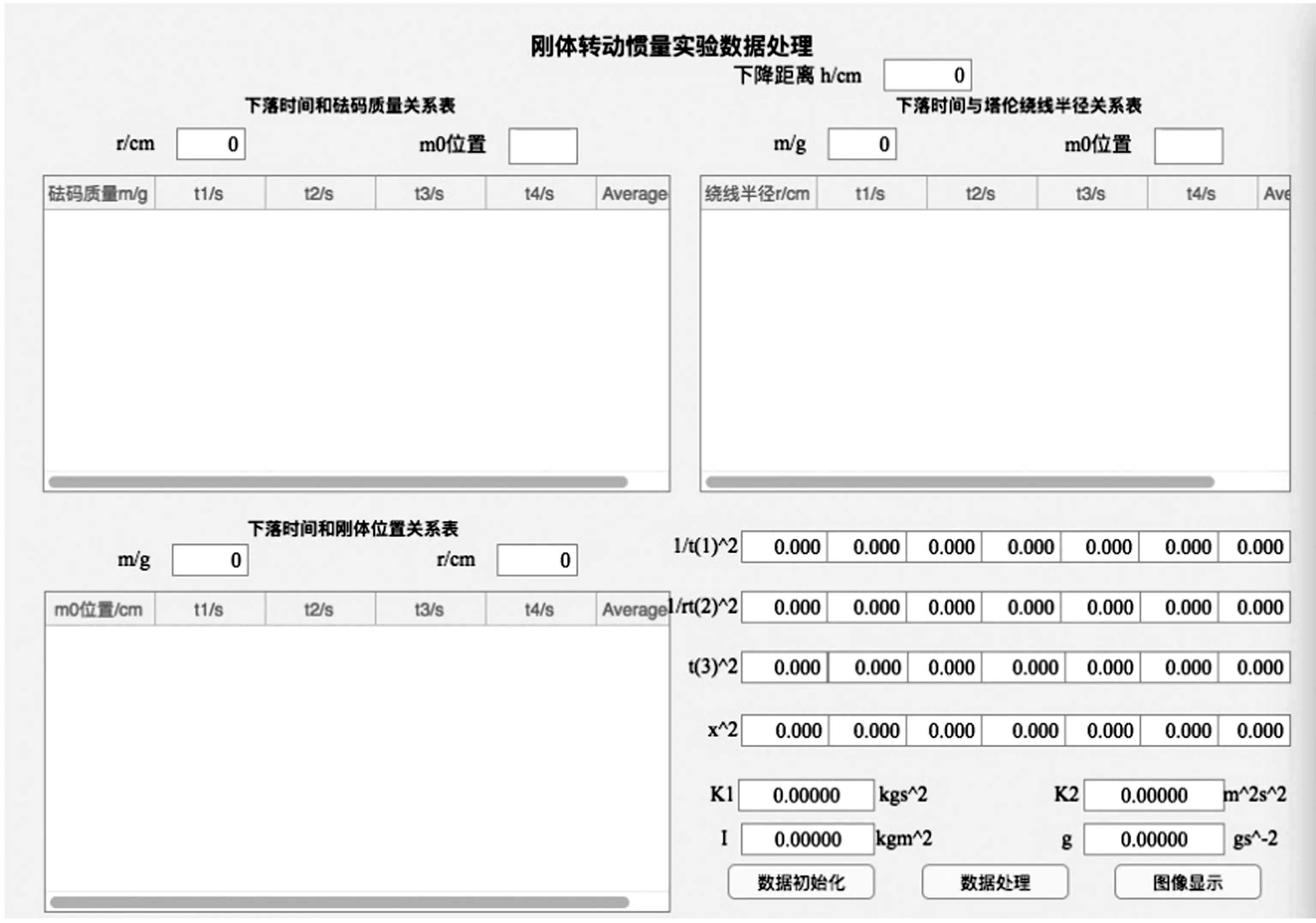
图1 MATLAB App Designer编程设计的软件界面图

4.2 实验数据处理示例

(1)点击“数据初始化”按钮，进行界面初始化.

(2)将实验测量的下降距离的实验数据h=85.00 cm，填入空格.MATLAB App Designer通过句柄获取下降距离的数据.

(3)根据式(7), 在表中将绕线半径的实验数据r=2.50 cm和m0位置(5,5′)填入相应空格内，保持r,h以及m0的位置不变，改变m,测出相应的下落时间t，并保持Mμ不变. 其中砝码质量m为5，10，15，20，25，30，35 g，相对应每个质量值测出下落时间t的平均值分别为16.49，11.32，9.29，8.04，7.14， 6.45，5.97 s，由MATLAB App Designer通过句柄获取数据，点击图像绘制按钮，采用最小二乘法拟合直线，拟合的结果如图2所示，直线的斜率为1.23，即

k1=1.23 kg·s2

截距为6.1×10-4，即

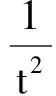
R1=0.999 76

线性拟合度很高.

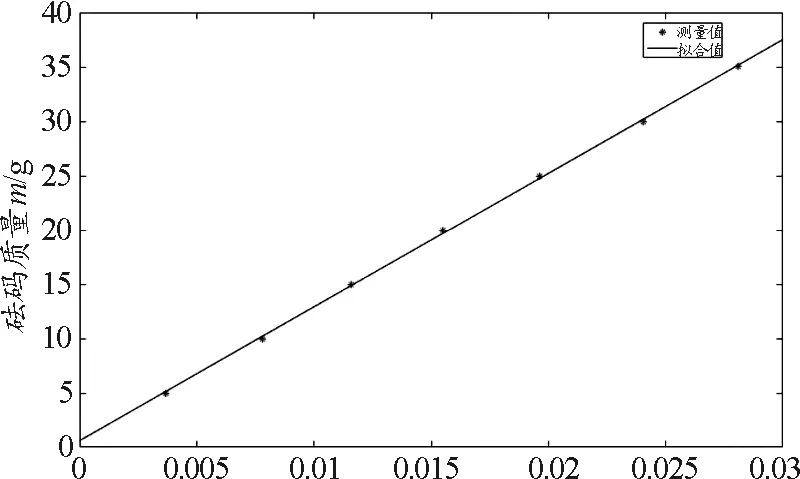
图2 MATLAB拟合下落时间和砝码质量关系图

(4)根据式(8), 改变绕线半径r，将砝码质量的实验数据20 g以及m0位置(5,5′)填入相应空格，取不同的半径值r分别为1，1.5，2，2.5，3 cm，填入相应空格，对应每个半径值测出的时间的平均值分别为20.05，13.51，10.07，8.04，6.68s，MATLAB App Designer通过句柄获取数据.点击图像绘制按钮，采用最小二乘法拟合直线，拟合的结果如图3所示，直线的斜率0.040 06，即

k2=4.006×10-2m2·s2

截距为2.2×10-4，即

相关系数

R2=0.999 86

线性拟合度很高.

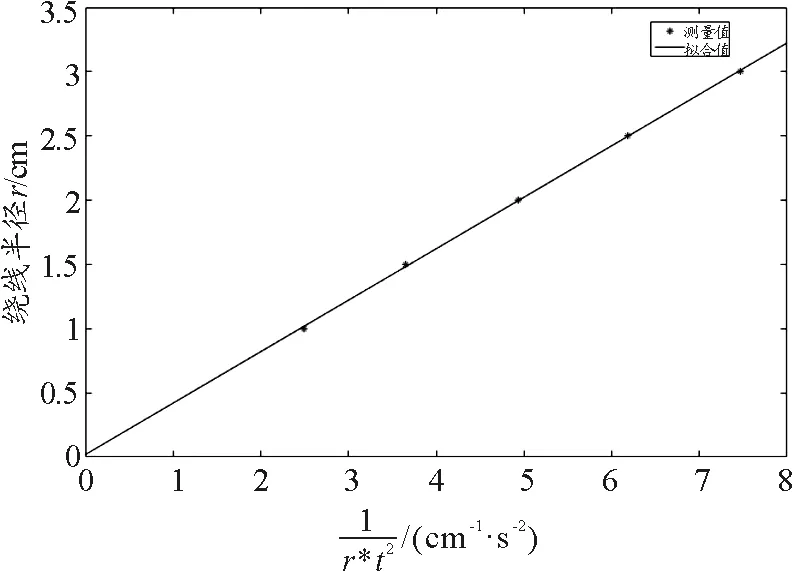
图3 MATLAB拟合半径与下落时间关系图

(5)对称地改变m0的位置，将实验数据m=20 g和半径r=2.50 cm，填入相应空格处，MATLAB App Designer通过句柄获取数据，其与转轴相距分别为0.324 1，0.573 2，0.823 2，1.073 2，1.323 2 cm，在相应位置填入实验的时间数据.点击图像绘制按钮得到x2-t2的图像，如图4所示，可以发现x2和t2之间满足线性关系(相关系数接近于1)，由此，在实验误差以及统计计算精度范围内验证了转动惯量的平行轴定理.

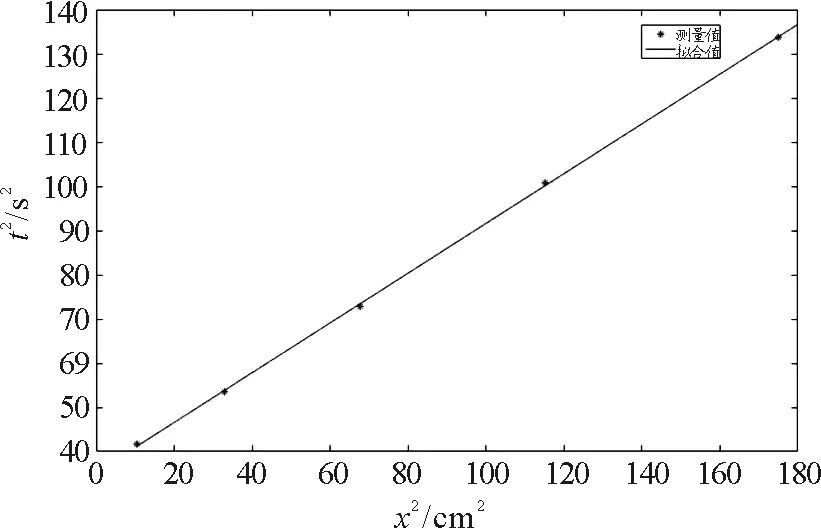
图4 MATLAB绘制验证平行轴定理图

I=4.4×10-3kg·m2

g=9.73 m·s-2

在传统实验教学中一般使用平均值法和逐差法进行数据处理，容易在做图和大量的计算过程中出错，使用此方法计算，不仅免去了大量的计算时间，避免了在手工计算中引入误差，而且本文中采用最小二乘法拟合方法，也使得到的实验处理结果更加精确.

5 结论

本文通过MATLAB App Designer的可视化编程处理实验数据，一方面改变了传统的实验数据处理方式，让学生从冗杂的数据处理过程中解放出来，另一方面提高了学生的自主性，加入编程的思想，锻炼了学生的逻辑思维和编程能力,并且使得数据处理结果更加精确,同时也提高了实验教学的有效性.此外，MATLAB软件下载十分简单，而且其编程也易于操作，最重要的是对于MATLAB App Designer来说不需要网络的连接，所以,将此方式在边疆少数民族地区进行推广可行性也很高，无论学生身居一线发达城市还是学于边疆地区，都可以同样享有此种教学方式，使优质的教学资源和方式得以共享，所有受教育者均能得到同等的享受优质教育资源和方式的机会[6]，因此，此教学方式的引入，不仅是教育形式和手段的更新，更是推进落实信息化教育和教育公平的重大进步.