电阻等效变换在直流电阻性电路中的应用

黄勇超

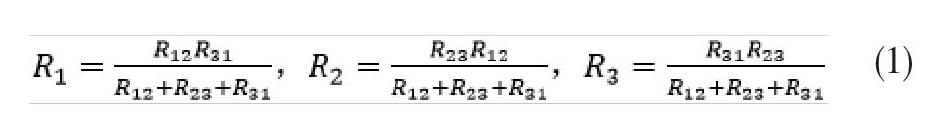
摘  要：三角形（△）联结与星形（Y）联结等效变换可以减少两个节点，对外电路的作用完全一样。复杂的直流电阻性电路中经常遇到三角形（△）联结的电阻，可以借助三角形（△）联结与星形（Y）联结的等效变换减少节点，从而简化计算。在求一个4个节点的电路实例中，经过两次从三角形（△）联结到星形（Y）联结的电阻等效变换，不用列线性方程组，通过简单的电阻串并联关系就可以求出各支路电流。

关键词：三角形（△）联结  星形（Y）联结  等效电阻

中图分类号：G642.3                               文献标识码：A                         文章编号：1672-3791（2019）03（b）-0045-02

Abstract： The equivalent transformation of triangle （△） connection and star （Y） connection can reduce two nodes， and the function of external circuit is exactly the same. In complex DC resistive circuits， the resistance of triangle （△） connection is often encountered. The equivalent transformation between triangle （△） connection and star （Y） connection can be used to reduce the nodes， thus simplifying the calculation. In an example of a four-node circuit， after two equivalent transformations of resistance from triangle （△） connection to star （Y） connection， the branch currents can be obtained by simple series-parallel connection of resistors without a set of linear equations.

Key Words： Triangle（△） connection; Star （Y） connection; Equivalent resistance

電路分析技术是高等院校电子类相关专业的一门重要基础课程，支路电流法、节点电压法、网孔电流法是常用的直流电阻性电路解法。如果电路节点过多，上述方法列出的线性方程组包含的线性方程过多，计算不容易。为了计算的方便，通常采用Matlab编程的矩阵计算[1]，也有些繁琐。

减少节点，无疑会减少线性方程。该文提供电阻的等效变换方法实际上就是利用三角形（△）联结与星形（Y）联结等效变换，减少电路节点的方法。通过三角形（△）联接与星形（Y）联接的等效变换，电路三角形（△）联接的3个节点变为星形（Y）联接的1个节点，线性方程组由3个线性方程减少到1个线性方程，求解过程就变得极为简单。

这种方法直接更改电路，思路清楚，比常用的其他几种直流电阻性电路解法简单好用。

1  三角形（△）联接等效变换为星形（Y）联接方法介绍

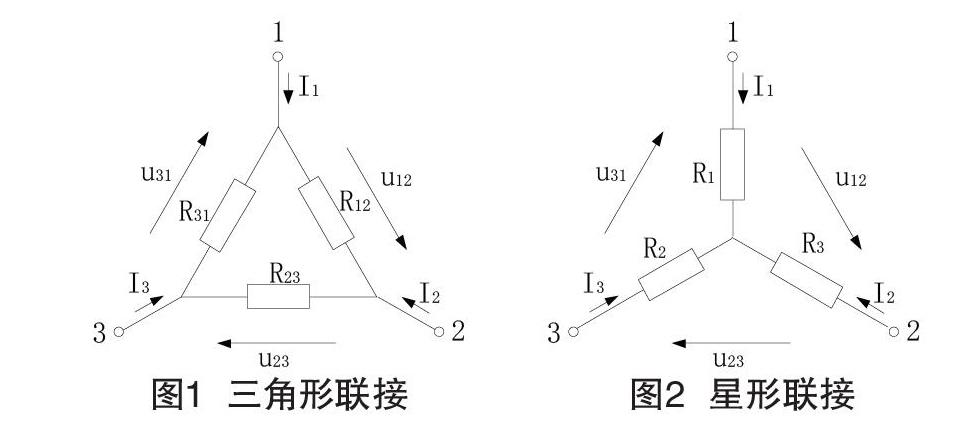
如图1所示的三角形（△）联接经过电阻的等效变换，变换成图2所示的星形（Y）联接。等效变换后，三端的电流与任何两端的电压在变换前后保持相同，对外电路的作用完全一样。

在图1和图2中，三角形（△）联接与星形（Y）联接的等效电阻变换公式为：

公式容易记忆。

2  电路实例

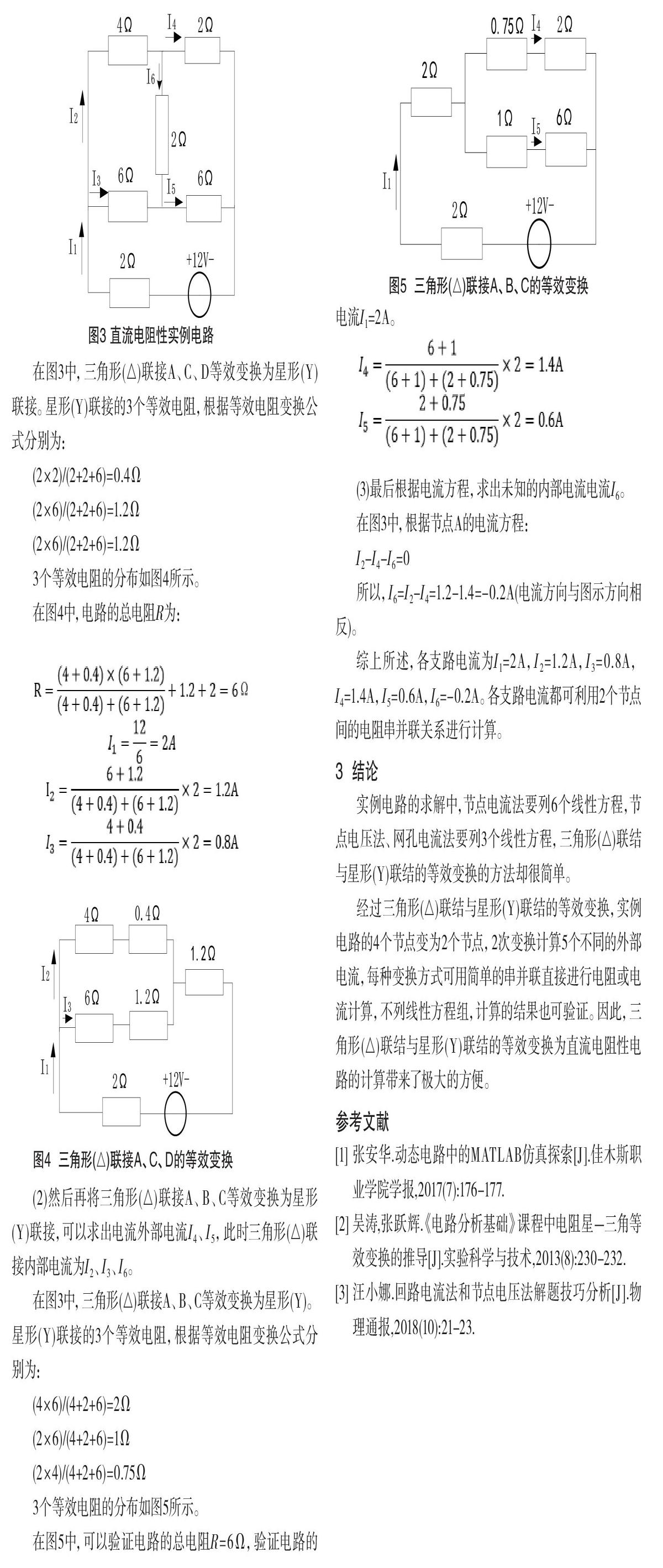
在图3所示的直流电阻性电路中，求各支路电流。电路中，节点A、B、C和A、C、D各构成一个三角形（△）联接。按常规方法都要用到基尔霍夫定律，列出电压方程和电流方程。

通过三角形（△）联接等效变换为星形（Y）联接的方法来解题，需要按下列3个步骤进行计算。

（1）先将三角形（△）联接ACD等效变换为星形（Y）联接，可以求出外部电流I1、I2、I3，此时，I4、I5、I6作为三角形（△）联接内部电流先不考虑。

在图3中，三角形（△）联接A、C、D等效变换为星形（Y）联接。星形（Y）联接的3个等效电阻，根据等效电阻变换公式分别为：

3个等效电阻的分布如图4所示。

在图4中，电路的总电阻R为：

（2）然后再将三角形（△）联接A、B、C等效变换为星形（Y）联接，可以求出电流外部电流I4、I5，此时三角形（△）联接内部电流为I2、I3、I6。

在图3中，三角形（△）联接A、B、C等效变换为星形（Y）。星形（Y）联接的3个等效电阻，根据等效电阻变换公式分别为：

3个等效电阻的分布如图5所示。

在图5中，可以验证电路的总电阻R=6Ω，验证电路的电流I1=2A。

（3）最后根据电流方程，求出未知的内部电流电流I6。

在图3中，根据节点A的电流方程：

所以，I6=I2-I4=1.2-1.4=-0.2A（电流方向与图示方向相反）。

综上所述，各支路电流为I1=2A，I2=1.2A，I3=0.8A，I4=1.4A，I5=0.6A，I6=-0.2A。各支路电流都可利用2个节点间的电阻串并联关系进行计算。

3  结论

实例电路的求解中，节点电流法要列6个线性方程，节点电压法、网孔电流法要列3个线性方程，三角形（△）联结与星形（Y）联结的等效变换的方法却很简单。

经过三角形（△）联结与星形（Y）联结的等效变换，实例电路的4个节点变为2个节点，2次变换计算5个不同的外部电流，每种变换方式可用简单的串并联直接进行电阻或电流计算，不列线性方程组，计算的结果也可验证。因此，三角形（△）联结与星形（Y）联结的等效变换为直流电阻性电路的计算带来了极大的方便。

参考文献

[1] 张安华.动态电路中的MATLAB仿真探索[J].佳木斯职业学院学报，2017（7）：176-177.

[2] 吴涛，张跃辉.《电路分析基础》课程中电阻星-三角等效变换的推导[J].实验科学与技术，2013（8）：230-232.

[3] 汪小娜.回路电流法和节点电压法解题技巧分析[J].物理通报，2018（10）：21-23.