牛顿环实验读数误差分析及改进方法研究
2019-06-17韩湖斌
韩湖斌

摘 要:从牛顿环实验原理出发,并根据读数显微镜的使用特点,系统地分析了读数测量误差的产生及代入曲率半径公式所造成的误差大小,分析原因及影响,并对其进行数学公式的推导确定其误差的大小,并由误差的组成来提出一种减小误差的方法,并对其进行实验探究。从实验中总结发现测量误差是主要因素, 从而提出牛顿环实验读数误差的改进方法,来提高实验精度,并得出结论n值取过大时虽然可以降低实验误差,但实验操作难度也随之上升,故将n取10,既可以降低实验误差,同时实验操作难度也不大。
关键词:牛顿环 曲率半径 实验精度
中图分类号:O4-34 文献标识码:A 文章编号:1672-3791(2019)03(a)-0227-03
Abstract: Based on the experimental principle of Newton's ring, and based on the characteristics of the reading microscope, the error of the reading measurement error and the error caused by the formula of the radius of curvature are analyzed systematically. The cause and influence are analyzed, and the mathematical formula is deduced to determine its The size of the error, and a method of reducing the error by the composition of the error, and experimental research. It is concluded from the experiment that the measurement error is the main factor, and the improved method of reading the error of Newton's ring experiment is proposed to improve the experimental precision. It is concluded that although the value of n is too large, the experimental error can be reduced, but the experimental operation is also difficult. Rising, so taking n to 10, can reduce the experimental error, and the experimental operation is not difficult.
Key Words: Newton's ring; Radius of curvature; Experimental precision
用牛顿环测量透镜曲率半径实验,是大学物理必学的实验之一,也是验证光的波动性的重要实验。因此,在目前光学实验中仍然占据重要的位置。但是多年来,实验误差较大的缺陷,影响了它的教学效果。这一问题,在使用读数显微镜读数方面所产生的误差是主要之一,学生在使用读数显微镜读数时,由于肉眼的观察读数时都会有误差的存在,进而影响了实验精度。如果在做实验前把产生误差的主要原因进行分析讲解,并寻找改进的方法,效果将会大大提高,该文就这些方面进行了分析讨论。
1 牛顿环实验理论原理
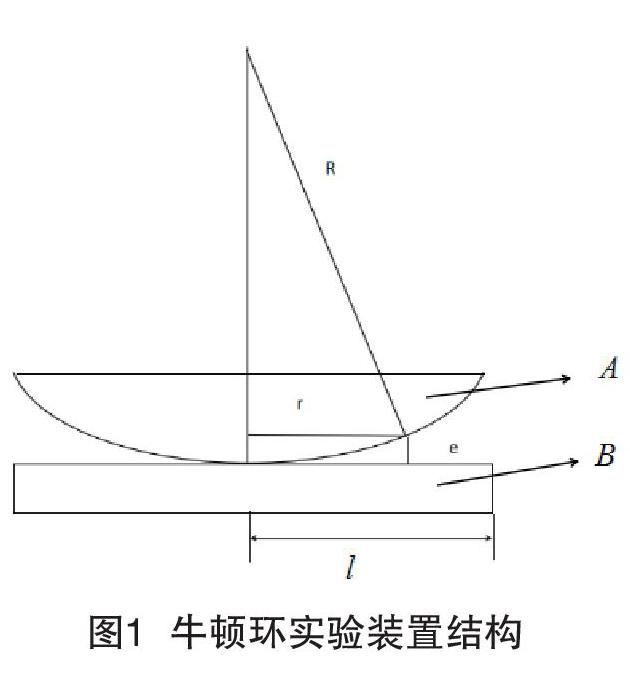
牛顿环实验装置结构如图1所示,在一块水平的玻璃片B上放一曲率半径R很大的平凸透镜A,上下2块玻璃用3个固定螺丝连接,用来调节A和B的相对位置,以改变牛顿环的形状和位置。
设透镜的曲率半径为R,与平板玻璃的接触点O距离r处的空气薄膜的厚度为e,由于平板玻璃上的表面的反射光线有半波损失,所以空气薄膜上下表面的反射光之间的光程差[1]:
2 牛顿环读数误差分析研究
2.1 读数显微镜读数时的定位误差
由公式(4)可知测量牛顿环干涉图像的第k级暗环直径时,需测得第k级暗环直径两端坐标值S和L,在使用读数显微镜进行测量的时候,每次读数都会由于暗环边缘的不准确性,而使得讀取的数值(S0和L0)和真实的数值(S*和L*)存在着一定的误差(△S和△L),尤其误差的来源将其称之为定位误差。故:S0=S*+△S,L0=L*+△L。
因此在计算第k级暗环直径时,就会引入定位误差。
由原dk=Sk-Lk,得dk0=Sk*-Lk*+△S-△L,将dk*=Sk*-Lk*,△dk=△S-△L,得:dk0=dk*+△dk。
其中Sk*和Lk*为第k级暗环直径两端真实值,dk*为第k级暗环直径真实值,△S和△L为读数第k级暗环直径两端值时进入的定位误差,△dk为第k级暗环直径误差值,dk0为第k级暗环直径实际读数值。
2.2 读数显微镜读数时的迭代误差
由于使用读数显微镜会对所测第k级直径产生的定位误差,把具有误差的直径值代入公式(4)而产生的误差值,由其产生原因将其称之为迭代误差。
3 牛顿环实验读数误差改进实验研究
光学玻璃应力测量实验的实验平台示意图如图1所示,由JCD3型读数显微镜,低压钠灯电源及JP20Na低压钠灯(波长为589.3nm)和牛顿环仪,A为平凸透镜,B为平板玻璃。
3.1 研究不同n值对实验结果的影响
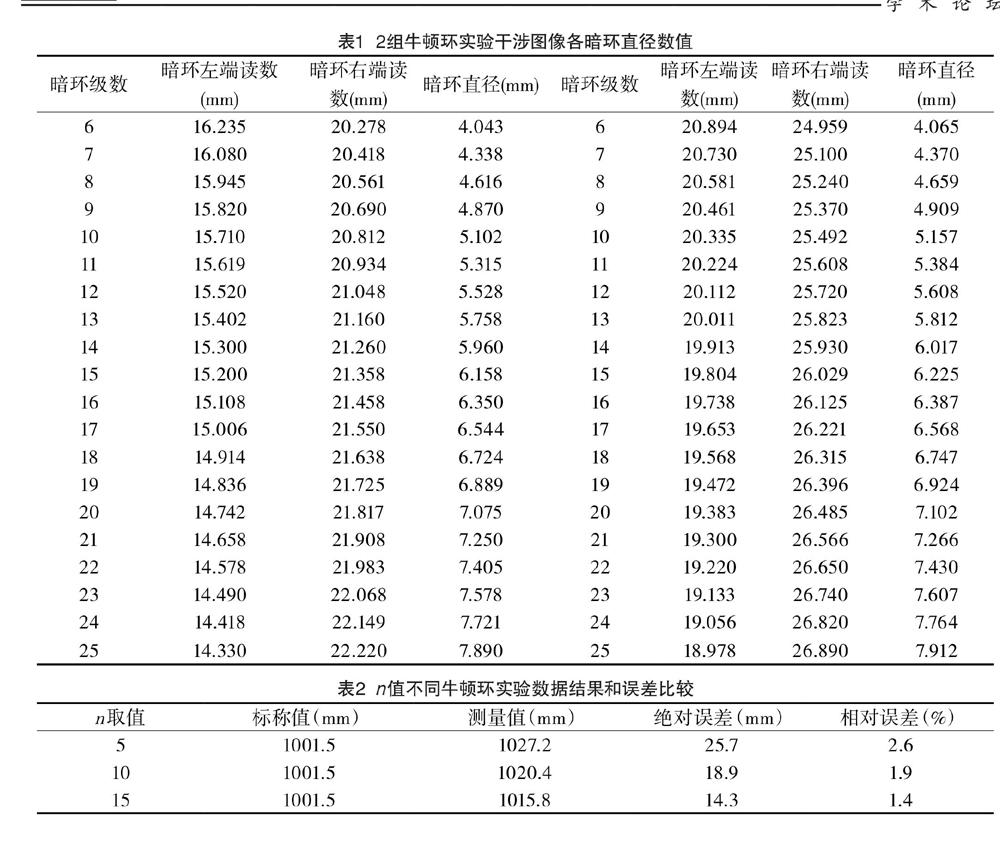
利用图1所示搭建的牛顿环实验平台进行实验测量,选取曲率半径为1001.5mm的牛顿环作为实验对象。记录各暗环的直径两端数值,并对实验数据处理时,分别取不同的n值,观察实验结果的影响。
3.2 分析原因
对表2数据进行分析,在牛顿环实验中,对n值是有所要求,从误差原理出发,n值越大,误差将越小,但在实际实验操作时,n值越大,会加大实验读数难度,故n不取太小也不取太大,故n取10时,即误差不是在2%以内,且降低了实验操作难度。
4 结语
该文探索研究影响牛顿环实验精度的因素之一,读数显微镜读数误差的影响,理论推导了读数测量误差的产生及代入曲率半径公式所造成的误差大小,分析原因及影响的大小,实验研究并提出增大 n的取值可以减小相对误差,并进行了实验验证。并得出结论n取值越大虽然可以减小实验误差但同时增加了实验的操作难度,故将n取值为10,验证结果误差保持在2%以内。
参考文献
[1] 炎正馨.大学物理实验教程[M].西安:西北工业大学出版社,2011:143-148.
[2] 马文蔚,周雨青,解希顺.物理学教程[M].北京:高等教育出版社,2006:198-199.
[3] 李平.牛顿环实验数据处理方法的回顾与讨论[J].物理与工程,2002(2):31-33.
[4] 王晓雄.利用Origin拟合方法处理牛顿环实验数据[J].大学物理实验,2011(4):73-74.
[5] 张卫国.数值计算方法[M].西安:西安电子科技大学出版社,2014:5-15.
[6] 郭長立,冯小强.光学玻璃挠曲刚度的光学测量方法研究[J].光学技术,2018,44(2):231-236.
[7] 李晨璞,谢革英,胡金江,等.基于LabVIEW的牛顿环实验动态仿真[J].实验室研究与探索,2013,32(6):97-101.
[8] 王家慧,盛毅,黄峰.牛顿环实验中系统误差分析[J].物理通报,2014(2):24-25,28.
[9] 张明霞.分振幅薄膜干涉-等厚干涉实验拓展[J].实验室研究与探索,2012,31(10):16-18.
[10] 王建岭.牛顿环实验误差的探讨[J].大学物理实验,2009,22(1):84-85,88.
[11] 左安友,翁祝林,李兴鳌.牛顿环实验误差分析及改进[J].湖北民族学院学报:自然科学版,2006(4):410-412.
[12] 郭长立.激光牛顿环现象分析及应用[J].实验室研究与探索,2011,30(6):18-20.
