基于多因子分析的无线传感器网络可靠性评估模型设计

芮立

摘  要： 采用判决反馈方法评估无线传感器网络时，仅从网络链路稳定性因素方面考虑，未考虑影响网络可靠性的多种因素，自适应能力和可靠性评估效果差。设计基于多因子分析的无线传感器网络可靠性评估模型，利用多因子分析过程将无线传感器网络复杂的变量关系简单化。由5个主指标与20个有相互关联的子指标建立无线传感器网络可靠性评估指标体系，通过主成分分析方法分析指标体系获取11个无线传感器网络可靠性指标主因子。将这些因子输入神经网络模型中，构建无线传感器神经网络可靠性评估模型，完成无线传感器网络可靠性评估。实验结果表明，该模型的可靠性评估精度均值为98%，该模型下的无线传感网络可靠性最高达到98%，极大提高了无线传感器的安全性能。

关键词： 多因子分析; 无线传感器; 可靠性评估; 主成分分析方法; 神经网络; 模型设计

中图分类号： TN915?34; TP311                 文献标识码： A                    文章编号： 1004?373X（2019）12?0156?05

Abstract： Only the stability factor of the network link is considered， and various factors affecting network reliability are not considered when the decision feedback method is used for wireless sensor network evaluation， resulting in poor adaptive ability and reliability evaluation effect. Therefore， a reliability evaluation model based on multi?factor analysis is designed for the wireless sensor network. The complex variable relationship of the wireless sensor network is simplified by using the multi?factor analysis process. The reliability evaluation index system of the wireless sensor network is built by using five main indexes and 20 interrelated sub?indexes. 11 main factors for the reliability index of the wireless sensor network are obtained by analyzing the index system with the principal component analysis method. These factors are input into the neural network model to build the reliability evaluation model of the wireless sensor neural network， so as to complete the reliability evaluation of the wireless sensor network. The experimental results show that the mean value for reliability evaluation accuracy of the model is 98%， and the maximum reliability of the wireless sensor network under the model reaches 98%， which can greatly improve the safety performance of the wireless sensor.

Keywords： multifactor analysis; wireless sensor; reliability evaluation; principal component analysis method; neural network; model design

0  引  言

無线传感网络（Wireless Sensor Network，WSN）被大范围应用在各个领域内[1]，WSN具备无线通信、成本低等优点。在确保WSN的可靠性的前提下，提高网络智能服务效率，同时以解决网络延迟、网络冗余与环境干扰等性能指标问题为目标建立WSN，并且各个性能指标相互制衡[2]。建立的WSN是否符合实际要求是由建立各个性能指标和传感器网络可靠性之间的关系验证。无线传感网络领域相关学者，越来越注重对网络可靠性的研究，设计高质量的无线网络可靠性评估模型具有重要的应用意义[3]。以往采用判决反馈方法评估无线传感器网络时，仅从网络链路稳定性因素方面考虑，未考虑影响网络可靠性的不同因素，自适应能力以及评估效果差。因此，本文从无线传感网络可靠性评估指标的多样性出发，设计有效的无线传感网络可靠性评估模型，增强无线传感器网络可靠性[4]。

1  基于多因子分析的无线传感器网络可靠性评估模型设计

1.1  多因子分析

为了全面评估无线传感器网络的稳定性问题，在无线传感器网络内收集大量的，能体现网络可靠性的多个变量，但无线传感器网络收集可靠性多变量大样本的过程导致数据收集负担加大。同时出现重复收集数据造成数据冗余问题，导致无线传感器网络的各个属性不能依据各个变量响应，存在差异的变量并不代表输电网的属性差异，因为大量变量之间在大部分情形下具有一定的关联性。反应无线传感器网络可靠性原变量中涵盖的关键信息，通过在大量指标中选取少量的综合性变量体现，将繁杂的变量关系简单化的过程为多因子分析[5]。

大量的原变量信息被少量的相互独立因子变量替代，这一替代过程为多因子分析需要考虑的方向，数学模型为：

采用因子分析将各初始变量划分成：

1） 公共因子由整个变量内少量的因子形成;

2） 特殊因子由各变量自身存在的不同因素形成。

1.2  评估指标的多因子分析

由5个主指标与20个有相互关联的子指标建立无线传感器网络可靠性评估指标体系[6]，同时各子指标与5个主指标相互关联。多因子分析某地区无线传感器网络的20组稳定性评估指标的样本数据。通过多因子分析了解到，指标样本的巴特利球度检验几率是0，检测统计量是131.051。由此可得相关系数矩阵与单元阵差异明显，并且依据KMO（Kaiser Meyer Olkin）的度量标准得知[7]，KMO<0.6时无法实施因子分析，本文KMO的值是0.826，能够进行因子分析。

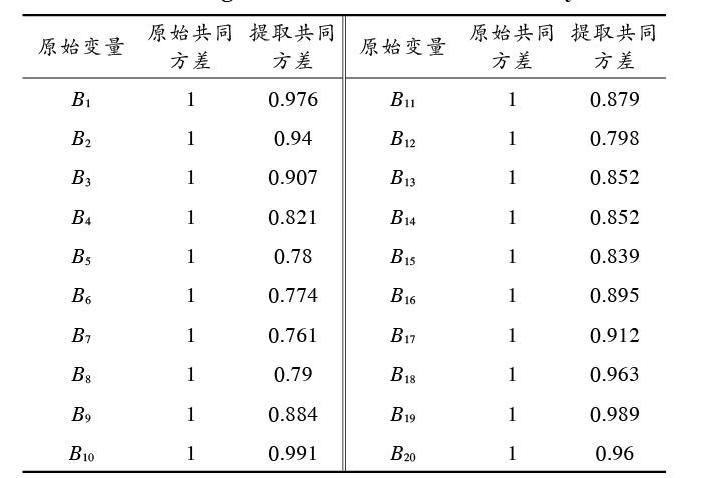
全部指标变量的共同方差数据由表1多因子分析的原始结果呈现。[B1?B20]为原始指标变量。采用因子分析方法获取原始解下指标变量共同方差用第2列描述，其是从原有20个指标变量中获取的20个特征值，那么可描述原指标变量的全部方差，指标变量的共同方差的平均值是1。第3列提取特征值时的共同方差是依据本文要求提取11个因子的条件提取，原始指标变量的数量比因子變量的数量多，所以各指标变量的共同度小于1。全部指标变量依据表1因子分析的原始结果得知共同方差均较高，不同指标变量信息被遗弃的几率较低，则因子提取的整体效果较好[8]。

表1  多因子分析的原始结果

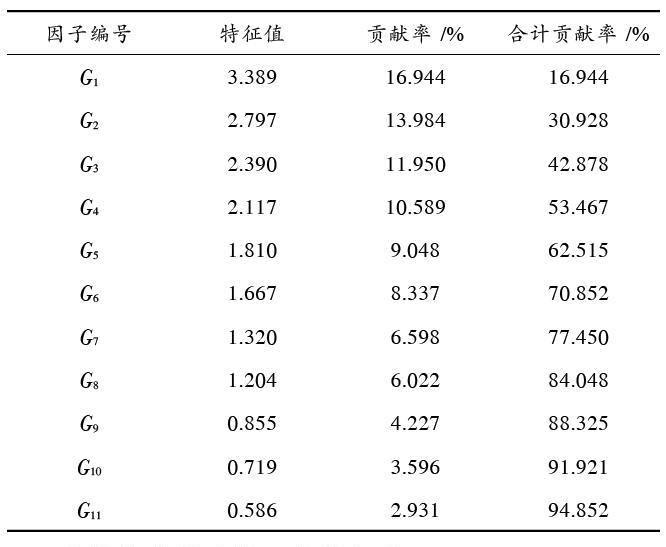
多因子分析贡献率如表2所示。通过多因子分析可行性运算转动后的因子载荷矩阵、贡献率等信息结果。前11个合计贡献率为94.852%，原20个指标变量大部分信息包括在提取的11个主因子内，因此可简化提取11个无线传感器网络可靠性指标主因子。

表2内，因子编号为提取的11个主因子变量。公共因子[Gj]中的各变量[Xi]的因子负荷量的平方总计为特征值，其也是式（1）内[dij]的平方总计。各因子解释原始数据的能力为因子贡献率，通过各因子解释的总方差度量，等同于各因子相关的因子负荷的平方和，该平方和为式（1）内[dij]的平方和。提取因子指标解释原指标变量的能力为合计贡献率，原始数据信息数量通过其体现。

评估指标之间的关联性随着指标变量的因子分析减少，无线传感器网络可靠性也可通过指标变量的因子分析结果，过滤低作用的指标变量，实现简化计算[9]，提高无线传感器网络评估的准确性。通过表1可得原指标变量的94.852%信息由11个主因子指标获取，同时降低了评估指标数量与评估成本，评估指标的科学性有所提升，为建立后续神经网络可靠性评估模型确立可靠分析基础。

表2  多因子分析贡献率

1.3  无线传感器网络可靠性评估

1.3.1  神经网络模型

随着人工神经网络（Artificial Neural Network，ANN）的不断发展，ANN受到无线传感器网络分析人员的关注。大量的神经元（Neural）相互连接形成的网络为ANN。ANN在信号处理机制中具有大范围并行分布处理等属性，相互连接的神经元间的连接权中反应了信息的存储过程[10]。

ANN具备神经网络运算能力、高度并行运算以及自适应性等优点，基于这些优点采用ANN可极大提高无线传感器网络可靠性运算自适应性和精度。

图1描述神经网络模型的结构，[W]为其输入层的单元数，[K]为隐含层的单元数，[N]是输出层的单元数。输入模式由各个隐单元运算1个核函数，所有核函数线性加权和为分类器的输出，则有：

训练神经网络模型内的各个子网满足神经网络的各个目的。一个多层神经网络结构为一个子网。图1内要求分配器将特定目标核函数分配给各子网，则依据不同子网的作用采用差异样本进行训练。之后子网输出数据特征通过分配器检索，获取的检索数据结果反馈给对应的子网。

图1  神经网络模型的结构

式中，期望输出和真实输出分别为[hrj]和[Qrj];网络输入向量的第[i]个元素为[irj]。

通过预处理器训练样本后，向神经网络模型中输入训练样本，可极大提高模型的训练效率。变换输入数据的域，即线性映射为预处理器。-1～1之间为输入数据的值，0.1～0.9之间为输出数据的值，训练神经网络时最靠近的域是输出数据的值。为增强训练算法的性能，将训练样本输入与输出数据的域通过处理器线性地转换成上述的域。结束训练后，最终输出的数据由后处理器进行线性转换到真实域中。

1.3.2  无线传感器神经网络可靠性评估模型

图2为依据第1.2节的多因子分析结果获取的11个无线传感器网络可靠性评估指标主因子，结合神经网络模型构建无线传感器网络可靠性评估模型，采用该模型实现考虑影响无线传感器网络可靠性的多种因子情况下网络可靠性的全面、准确评估。

2  实验分析

实验测试本文模型评估某无线传感器网络可靠性的有效性时，对比分析本文模型、马尔可夫模型与云模型对无线传感网络评估的实验网络可靠性和传感器密度的关系，结果如图3所示。

图2  可靠评估模型构建流程

圖3  可靠性和传感器密度关系

分析图3可知，3种模型评估的无线传感器网络可靠性随着传感器密度增大而增大;本文模型评估的网络可靠性平均值为49%，最高可靠性达到98%，马尔可夫模型和云模型评估的网络可靠性平均值为43.5%和25%，本文模型评估的无线传感器网络可靠性均值比其他两种模型分别高5.5%和24%，说明本文模型评估下的无线网络可靠性较高。

无线传感网络节点存活数目随时间变化越稳定，时间越长，节点存活数目越高，说明无线传感网络越稳定，当无线传感器网络大小分别为100 m×100 m，200 m×200 m时，实验检测3种模型下无线传感网络节点存活数目与时间的对比情况如图4所示。

实验统计3种模型对上述两种无线传感器网络进行可靠性评估的时间和精度情况，结果分别如表3与表4所示。

表3  3种模型可靠性评估时间

                

图4  节点存活数目随时间变化状况

分析表3中3种模型对两种无线传感网络实施可靠性评估的时间得知，无线传感器网络大小为100 m×100 m时，本文模型可靠性评估时间均值比马尔可夫模型、云模型可靠性评估时间均值分别低6.72 s，7.5 s;无线传感网络大小为200 m×200 m时，本文模型可靠性评估时间均值比马尔可夫模型、云模型可靠性评估时间均值分别低7.26 s，8.5 s，说明本文模型对无线传感器网络实时可靠性评估用时最短。

分析表4得知，无线传感器网络大小为100 m×100 m时，本文模型可靠性评估精度均值比马尔可夫模型、云模型可靠性评估精度均值分别高12%，21%;无线传感器网络大小为200 m×200 m时，本文模型可靠性评估精度的平均值比马尔可夫模型、云模型可靠性评估精度的平均值分别高13%，21%，说明本文模型更能精准完成无线传感器网络可靠性评估。

3  结  论

为了从多种角度充分考虑影响无线传感网络可靠性的因素，提高无线传感器网络可靠性评估的精度和全面性，本文设计基于多因子分析的无线传感器可靠性评估模型。通过5个主指标与20个有相互关联的子指标建立的无线传感器网络可靠性评估指标体系后，通过主成分分析方法获取11个无线传感器网络可靠性指标主因子，达到过滤低作用指标变量，降低评估指标数量和评估成本，提高评估指标科学性的目的;将11个主因子作为神经网络的输入值，构建无线传感器神经网络可靠性评估模型，能准确评估无线传感器网络的可靠性。

参考文献

[1] 刘逻，哈清华，王安邦.基于FABP的软件可靠性增长模型[J].计算机仿真，2015，32（6）：440?446.

LIU Luo， HA Qinghua， WANG Anbang. Software reliability growth model based on FABP [J]. Computer simulation， 2015， 32（6）： 440?446.

[2] 刘创，王珺，杜蔚琪，等.基于网络编码的无线传感器网络多径路由模型分析[J].计算机工程，2016，42（4）：37?43.

LIU Chuang， WANG Jun， DU Weiqi， et al. Analysis of multipath routing model in wireless sensor network based on network coding [J]. Computer engineering， 2016， 42（4）： 37?43.

[3] 赵治国，谭敏生，夏石莹，等.基于时间因素的无线传感网络信任模型[J].计算机工程与设计，2017，38（4）：883?887.

ZHAO Zhiguo， TAN Minsheng， XIA Shiying， et al. Wireless sensor network trust model based on time factor [J]. Computer engineering and design， 2017， 38（4）： 883?887.

[4] 李建平，王晓凯.基于模糊神经网络的无线传感器网络可靠性评估[J].计算机应用，2016，36（z2）：69?72.

LI Jianping， WANG Xiaokai. WSN reliability evaluation based on fuzzy neural network [J]. Journal of computer applications， 2016， 36（S2）： 69?72.

[5] 程红霞，谭新莲.多次重传的链状无线传感网络可靠性分析[J].计算机工程与应用，2018，54（5）：79?84.

CHENG Hongxia， TAN Xinlian. Analysis of reliability for wireless sensor network with chain topology based on multiple retransmission strategy [J]. Computer engineering and applications， 2018， 54（5）： 79?84.

[6] 王珺，杜蔚琪，刘辉，等.一种基于相交多径网络编码模型的无线传感网多径路由协议[J].计算机科学，2016，43（11）：135?141.

WANG Jun， DU Weiqi， LIU Hui， et al. Multipath routing protocol based on braid?multipath network coding model for wireless sensor networks [J]. Computer science， 2016， 43（11）： 135?141.

[7] 王枫，祁彦鹏，傅正财.面向开关的复杂配电网可靠性评估简化模型[J].电力系统及其自动化学报，2015，27（2）：57?63.

WANG Feng， QI Yanpeng， FU Zhengcai. Switch oriented simplified model of reliability evaluation of complex distribution system [J]. Proceedings of the CSU?EPSA， 2015， 27（2）： 57?63.

[8] 马丽瑛，李剑波，王智颖，等.基于无线传感器网络的可靠性模型及上界[J].数学的实践与认识，2016，46（12）：130?138.

MA Liying， LI Jianbo， WANG Zhiying， et al. The math model and the upper bound of the network reliability based on the wireless sensor network [J]. Mathematics in practice and theory， 2016， 46（12）： 130?138.

[9] 唐清明，趙菊敏，李灯熬，等.基于组合指标的无线传感器网络安全路由算法[J].电视技术，2016，40（11）：59?63.

TANG Qingming， ZHAO Jumin， LI Dengao， et al. Combination routing metric based routing algorithm for WSN [J]. Video engineering， 2016， 40（11）： 59?63.

[10] 杨栋，李书琴.自适应速率规划的无线传感器网络传输优化模型[J].计算机工程与设计，2017，38（5）：1148?1151.

YANG Dong， LI Shuqin. Wireless sensor network transmission optimization model based on adaptive rate planning [J]. Computer engineering and design， 2017， 38（5）： 1148?1151.