基于广义Hoek-Brown强度准则的岩质边坡稳定性分析

陶 纬，孙树林，2，李 方，胡 昭，宗 岩

(1.河海大学地质工程系，南京 211100； 2.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098； 3.江苏省南京工程高等职业学校，南京 211135)

0 引言

岩质边坡在我国各地的各种工程中非常常见。由于长期的地质构造活动以及风化等外力作用，岩质边坡可能会存在一些大小各异的裂隙、节理等结构面，这些结构面甚至对边坡稳定性起到控制作用。

目前，国内外已有许多文献提供了多种分析方法，提出了不同的稳定性分析理论。例如应用广泛的各种极限分析法，强度折减法，数值模拟法(有限元，离散元等)，比较注重统计与数据分析的模糊数法，随机事件概率分析法以及神经网络等方法[1-6]。

极限分析法实际上包含了不少种类，除了比较基础的利用几何关系对比滑动与阻滑力的关系以及力矩之外[7]。现有的许多研究工作发展出了新的内容，例如通过对极限分析中几何条件的变化探究边坡、裂隙等的几何条件、贯通性等对滑坡形成的影响[8]。

不少专家学者提出了岩质边坡各种分析带有裂隙的边坡稳定性的方法。其中Chen等人利用假定发生滑动时产生的能量平衡进行极限分析上限法来分析岩质边坡的稳定性[9]。Utili将该方法应用于带有垂直裂隙的边坡，同时还考虑了边坡含水条件下的稳定性分析[10]。然而多数方法进行岩质边坡的稳定性分析时，并未有效地利用对岩体性质的评价，而是将岩质边坡作为岩块进行处理，利用摩尔库仑强度模型中的内摩擦角与粘聚力进行分析计算。

本文根据Yang等人提出的方法[11]将广义Hoek-brown强度准则与岩体的GSI指标引入极限分析上限法，对带有垂直裂隙的岩质边坡进行非线性二维稳定性分析，从地质工程角度对带有裂隙的岩质边坡进行稳定性评价，同时还分别考虑了裂隙中水的扬压力以及作用于边坡坡顶的外荷载的影响，并采用拟静力法模拟地震对于岩质边坡稳定的影响。而该方法引入的安全系数与传统定义为最大剪切应力与动员剪应力之比的安全系数是完全等价的，两者都可以用来表征边坡的稳定性[12]。

本文的创新点在于：①提出了一个可以将岩体质量评价应用于带有裂隙的岩质边坡稳定性分析中的方法，避免了上限法中岩体不同位置粘聚力和内摩擦角差距甚远而难以取值的问题；②应用该方法可以对具有多裂隙的岩质边坡进行对比，比较不同裂隙对边坡稳定性的影响，从而确定最危险的滑动体。

1 广义Hoek-brown强度理论简介

本文对于具体的工程边坡的稳定性评价，是建立在事先对岩体质量通过特定的方法进行评价之上的。例如Bieniawski提出的RMR分类，Barton等人提出的Q分类，Hoek等人提出的GSI等。

自1980年Hoek和Brown，提出用于节理岩体参数的评估方法和广义Hoek-Brown强度准则后30 多年来，许多专家学者一直致力于该方法的进一步修正完善，经过7次较大改进。目前强度准则的表达式为[13]:

(1)

(2)

式中GSI指的是Hoek于1995年提出的一种岩体分类标准。该标准根据岩块的块度和不连续面的状况等方面的评价得出，具体获取方法有图表法，基于现场观测的软件处理法以及结构面摄影，节理统计分析以及综合分析法[14-16]。mi为材料常数，是通过对完整岩石经进行三轴压缩试验而得到的，其取值方法来自于对大量工程实例的总结，同时为了保证其可靠性亦可以通过对微观结构的观察来确定其取值[17]。D为考虑工程扰动因素的岩体弱化因子，为0～1，为计算方便本文采用D=0。

现有的大量运用广义Hoek-Brown准则的案例和方法，大多采用极限平衡法，从力以及力矩的角度对稳定系数进行计算。例如对部分乃至全部参数进行模糊数学分析,以分析GSI、mi等参数在岩坡稳定性分析中的可靠度、敏感性、合理的权重设置以及折减法中的折减系数选择[17]。而本文则是将该准则引入极限分析的上限法中使用。

2 模型的建立

本文所研究的边坡(图1)的几何关系为：边坡的高度为H，其坡面与水平地面的夹角为β，其坡顶面与水平面的夹角为α，这两个角的大小关系为0<α<β<π/2。岩体的质量指标为GSI以及mi值，岩块的平均重度为γ，其单轴抗压强度为σc，内摩擦角为φ。滑裂面由等式r(θ)=r1e(tanφ(θ-θ1))定义，并且终端与坡脚点相交。A点为滑移面与坡顶面的交点，B点为坡脚，C点为坡顶点，D点为垂直裂隙与滑动面的交点，E点为垂直裂隙与坡顶面的交点。裂隙无填充，并且深入到滑动面上，其总长度为Hf，且裂隙后端岩块不发生滑动。ω为边坡发生滑动时的虚拟速度场的角速度。根据图1中的几何关系可以推导出坡A与C点的距离L1，A与E点的距离L2，坡顶到地面高程H与垂直裂隙被滑动面与坡顶所截取长度Hf：

(3)

L2=r1{cosθ1-exp[tanφ(θf-θ1)]cosθf}

(4)

(5)

(6)

该裂隙内含有裂隙水，其水位高程到不连续面的高度差为Hw，在坡顶部受到密度为q的均布荷载，为了模拟地震中地面加速度引起的潜在惯性力，引入水平和竖向静地震力，假定这些力与作用力次数、水平和垂直平均地震系数Kh和Kv成正比[22]。

图1 边坡滑动机制Figure 1 Slope sliding mechanism

3 极限平衡上限法

根据运动学方法中关于屈服的理论，在图1所示的平面中，如满足一定的条件，那么边坡在外布荷载的作用下是稳定的[12]，稳定系数上限如下：

(7)

式中Pext为滑坡过程中外部荷载做功(即沿着不连续面耗散的能量)，Pd是最大阻滑力(以延滑动面的摩擦为主)做功功率。

(8)

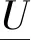
分为：

Pext=P1-P2-P3-(P4-P5-P6)

(9)

式中：P1、P2、P3、P4、P5、P6分别代表图1中P-A-B、P-A-C、P-C-B、P-A-D、P-A-E、P-E-D假设块体滑动过程中的重力做功功率，则根据几何关系可得Pext为真实存在并发生滑动的部分，即C-B-D-E的重力做功功率。根据S. Utili[10]，将块体分为无数个微元体。将(8)和(9)表示为以下微元和积分关系：

(10)

式中：|xp-xg|代表P点与所求滑块重心之间的水平距离，Ai为所求微元体的面积。为了便于计算，将p点x坐标设为0可得：

Pi=Aixg

(11)

式中：Ai为所求块体面积，xg为其重心的x坐标，对于需要去除的三角形块体，例如P-A-C块体，则有：

(12)

式中：xi1和xi2分别代表三角形块体中除P点外的其余两点横坐标，例如P-A-C的A与C点横坐标。这些坐标可由r1经变换得到，对于非三角形块体的重心可通过重心的计算公式得到。

根据S. UTILI 的计算方式[10]及 (11)和 (12)可解出具体的P1～P6块体假设滑动中重力做功功率表达式为：

(13)

(14)

(15)

(16)

(17)

(18)

根据Mounir Belghali[12]可知抗滑的阻力在滑动过程中的做功功率表达式：

(19)

用同样的方法计算Pd2，同Pd1类似Pd2中也可以提取出c，ω，和r1，则将式(7)～(17)结合起来可以得到：

(20)

4 基于广义Hoek-brown准则的边坡稳定性上限法公式推导

4.1 Kh=Kv=Hw=q=0时的岩质边坡稳定性分析

式(20)基于摩尔库伦强度准则将边坡的整个岩体视作一均质各向同性的单一材料。该方法在一定程度上忽略了岩体是由岩块和结构面之间的相互关系，即c的取值大多是由室内试验对局部岩体测试得到，难以反映整个边坡岩体的结构构造对稳定性的影响。

为了将岩体质量指标引入上限法的计算。根据Yang提出的换算公式[14，23-24]，可以近似地采用Hoek-brown准则的参数来表示岩体中粘聚力c和单轴抗压强度σc之间的关系。

(21)

将式(21)代入于式(20)的中取代粘聚力c，便可实现将反映岩体整体质量的GSI指标引入进稳定性分析，则得到如下关系：

(22)

上述公式必须满足一定的条件，以对边坡的形状做出一定的限制。除Mounir Belghali[12]提出的边坡整体形状限制外，对垂直裂隙的位置也做出一定的限制，总体如下：

0<θ1<θf<θ2<π-β

(23)

sin(β+θ1)-exp[2tanφ(θ-θ1)]sin(β+θ2)>0

r1>0

即摩擦角大于0，限制滑动面的圆心处于边坡外，滑动面初始半径大于0，保证裂隙与滑动面相交等。

在某一确定的岩质边坡中，只有θ1和θ2两个变量不是确定的，即对特定边坡来说存在一组θ1和θ2的组合使得稳定系数F最小，将F作为因变量，θ1和θ2作为自变量，组成二元函数并绘制其图像(图2为θ1和θ2分别在0～π/2,与π/3～2/3π的图像，其中过高的部分及其以外为不满足约束条件的部分)，观察其在约束条件范围内的极值点，并计算出其在相应条件下所得到的最小值Fmin。

图2 F关于θ1和θ2的函数图像Figure 2 F functional graphs of θ1 and θ2

4.2 Kh≠0,Kv≠0,Hw=q=0时的岩质边坡稳定性分析

在地震分析中，本文采用拟静力法[7，11，25-29]。由于地震作用对滑坡体的主要影响方向在水平方向，故使用水平地震系数Kh，忽略数值地震系数Kv。已知地震力是作用在整个滑动体上的体力，为了模拟水平地震力的作用，将其类比于重力作用，根据水平地震系数的含义可将其类比容重γ，而其作用方向与重力垂直，则|xp-xg|对应取|yp-yg|,将式(11)修改为以下形式来达到以一静力模拟地震作用的效果:

(24)

同理类比式(13)～(19)，将图1中的几何关系代入式(24)可得：

(25)

(26)

(27)

(28)

(29)

(30)

以上各式即为假设各块体在滑动时地震力做功功率。将(24)-(30)带入(22)得：

(31)

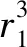
表1 应用拟静力法计算不同地震系数下的稳定系数

从表中可看出，地震越强则稳定性就越弱。

4.3 Kh≠0,Kv≠0,Hw≠0,q≠0时的岩质边坡稳定性分析响

裂隙水密度取1.0 g/cm3。本文主要计算裂隙内的水产生的侧向水压力的影响，根据Hw处的水压力计算公式可知做功与块体体积无关，与水位深度相关，为一随深度线性变化的水平荷载。参照式(24)，根据水压力大小的公式[10]，取系数为ω，Hw以及水的密度γw取1.0，整体面积被压缩成一条线。结合荷载的线性分布与三角形面积公式求功率如下：

(32)

(33)

倘若均布荷载不垂直，则其水平分量可以分解裂隙水作用在裂隙投影在垂直方向和水平方向上。同时考虑坡顶均布荷载对岩质边坡做的功Pq也为沿着坡顶分布的竖直线荷载，对式(10)(11)进行再次变形，同水压力推导，将荷载作用线视作一无限窄的面，成为：

(34)

用几何关系式求出xL和yL代入上式得：

(35)

同Pq1的计算方法可计算Pq2，有Pq=Pq2-Pq1为均布荷载对滑坡体部分做功。将Pw+Pq1-Pq2加到式(19)的分母部分即可达到综合考虑地震力，裂隙水压力以及均布荷载作用，其最终结果为得到公式：

(36)

4.4 L2>L1的稳定性分析

由于裂隙并不会只出现在坡顶，也有可能其顶端延伸至坡面处，即可能出现L2>L1的情况(图3)，在此情况下可以利用以上各公式的方法中将块体E-C-F的部分减去即可，但是必须注意由于均布荷载作用在坡顶，而坡顶部分到裂隙与坡面相交处之间的部分不滑动，故可忽略均布荷载带来的影响，结果如下：

图3 垂直裂隙与坡面相交几何示意Figure 3 Geometric diagram of intersection betweenvertical fissures and slope surface

(37)

(38)

在式(31)中减去该块体的相应的部分的重力做功以及地震影响即可。

5 算例分析

为了比较基于广义Hoek-Brown强度准则上限法和极限分析上限法的异同，故分别利用二者对一算例进行分析。现有一岩质边坡，其边坡坡度接近60°，坡顶坡度5°，坡高10m，假设其距离坡顶边缘2m处因工程建设的缘故产生一垂直无填充卸荷裂隙，且岩体本身存在着少量不连续的微型、小型结构面。岩体的岩块成分为粉砂岩，岩体结构为块状，完整度高，σc为35 MPa，mi为7，岩体重度为25 000 N/m3，因边坡爆破开挖抑或是建筑前修整发生扰动，扰动因子D=0.1，根据式(32)-(33)中的方法对GSI进行取值，由扰动因子D=0.1可认为其结构为仅有轻微扰动。风化程度为微风化，GSI取60。

计算其等效内摩擦角为32°，粘聚力c=2.0MPa，弹性模量Em=9 GPa，地震影响系数Kv忽略，Kh为0.1，无裂隙水，对其稳定性使广义Hoek-brown方法进行计算F以及使用摩尔库伦强度准则式(16)的Fc进行比较。

同时为了了解不同θ1和θ2的组合(即不同形态的滑动面)对稳定性的影响，分别计算不同合理θ1和θ2条件下F和Fc的对比(θ1和θ2均满足约束条件)。经计算其中θ1的大致合理在50°～70°，θ2为80°～90°。其结果如下表：

表2 广义Hoek-brown上限法和一般极限分析上限法比较

经计算，二者的差值大概在10% 左右，用基于广义Hoek-Brown强度准则的上限法计算出的结果稍微保守一些，计算的最小值在12和14左右。究其原因，在于GSI取值中考虑到岩体内部存在的几组不平行节理的影响而取值比较考虑安全，而一般的极限分析上限法因为粘聚力c等参数来源于实验室对岩石块体的试验，并不考虑岩体内可能存在的多组微、小型结构面的影响。结果证明，该方法行之有效，只要合理地对GSI的取值就可以得到有效的分析结果，同时为了达到更高的安全度可以对GSI指标进行一定的折减处理再进行计算。需要注意的是F和Fc并不是单纯随着某一趋势增长或减小的，在合理范围内可以取到最小值。倘若计算的岩质边坡存在各种不同的工况，则可将式(32)中的所需内容填入程序并计算。同时本方法对于一些不适用c和φ值进行计算的场合可以起到不错的效果。

为了比较该方法对于裂隙中含水的情况下产生的影响，故假设本算例中的裂隙含有裂隙水，其高度为Hw。为方便计算取Hw=Hf，在计算过程中发现fw的值非常小，仅有7.5×10-7左右，几乎对计算结果不产生影响。究其原因是裂隙深度较小，水压力作用范围仅裂隙面且均值较小之故。

此外，为研究坡顶布置有地基等荷载的情况下该算例的稳定情况，在本算例中添加一均布荷载，计算其分布密度q=2 000 kPa及改变Kh=0.2时的影响。经过计算得到以下结果：

表3 广义Hoek-brown上限法在q=1 000kPa及Kh=0.2时的稳定系数

从表3可以看出，竖向均布荷载和地震作用对于岩质边坡稳定性的影响有非常大的不同，荷载作用下稳定性降低且其极值所在的θ1和θ2范围会发生变化，且造成的稳定性变化幅度远不如地震影响大，而地震系数在仅仅增加0.1的情况下其稳定系数计算值发生了非常大的变化，但总体变化趋势以及预计取得极值的范围没有产生很大的变化。

6 讨论

在应用该方法进行岩质边坡稳定性分析时，需要注意谨慎地选取GSI的值。因为该指标具有一定的主观性，需要一定的取值经验。但是同时其亦有优越性，对于局部岩体结构差的情况下可以对数值按照标准降低GSI进行折减。值得注意的是GSI指标对应的变化涉及到岩体结构的整体变化，故少量的折减都会带来比较大的安全度提高，故折减系数最好不要取得太大。一般的基于摩尔库伦强度准则的上限法中，强度参数尤其是粘聚力c，往往是通过对岩体试样进行室内试验所得出的，并不考虑结构面的影响，却代表了整个边坡或者整个地层的参数，这样对于具有特殊结构岩体就难以确定合适的值以应用于整个岩体。例如算例中的岩体具有少量微、小型结构面，虽然对完整性影响不大，但是不能忽略，此时对于c的选择就比较困难了。故本文使用的方法可以较好地解决这种问题。

该方法还可应用在有多条卸荷裂隙或者是倾斜分布的裂隙边坡以及边坡或其他地质体上存在的具有滑动可能性的危岩体稳定性分析。对多条裂隙分析，可以对每一条裂隙前部进行稳定性计算，取最小值所在的裂隙作为最危险的不连续面发展处。对于倾斜裂隙，可以利用几何关系将垂直的裂隙的稳定性分析方法进行转化从而计算得出结果。

此外，应用该准则亦可以结合大量现有的研究进一步进行研究。例如在广义Hoek-Brown准则上建立关于GSI和边坡稳定的概率模型以及基于大量工程实例构建神经网络等，可以考虑对卸载边坡进行分析的时候引入岩石损伤的本构模型进行研究[31]，将大量现有工作的优势和极限分析上限法与Hoek-Brown准则的优势以及应用结合起来，为Hoek-brown准则的应用拓宽思路，并不局限于单纯地求取稳定性参数而是对方法和参数进行合理全面地分析。同时亦可从边坡加固或支护措施的角度分析所需的加固或支护条件，具有十分广阔的应用前景。

7 结论

本文在极限分析的上限法的基础上引入了Hoek-brown强度准则和GSI岩体质量指标来分析带有垂直裂隙的岩质边坡的稳定性。并对地震、均布荷载以及裂隙水扬压力等不同工况下的稳定性进行了分析。通过案例计算，证明使用该方法分析带有垂直裂隙岩质边坡与极限分析法的差距10%左右，同时还发现均布荷载作用于地震力的作用造成稳定性变化的差异。由于该方法比一般的极限分析上限法更注重岩体结构问题，故能够更全面地分析岩质边坡的稳定性。