基于宽度优先的网络最大流求解算法
2019-06-14邵丽萍赵礼峰
邵丽萍,赵礼峰
(南京邮电大学 理学院,江苏 南京 210023)
0 引 言
网络最大流问题是一个属于图论和运筹学的问题[1-3]。最初Fulkerson等[4]在处理最大流问题时,运用了图论的方法。后来,在1956年Ford-Fulkerson给出了求最大流问题的标号算法[5];Dinic(1970),Edmonds和Karp(1972)独立提出了改进Ford-Fulkerson算法的思想:每次都沿最短(即弧数最少的)增广链进行增广,即最短增广链算法[6-7];Karzanov(1974)提出了预流的概念,基于预流的概念,进一步提出了预流推进的算法;Cherkassky提出了最高标号预流推进算法[8]。这些经典的算法是研究大规模网络的基础。在这些研究之后,很多学者针对特殊网络或经典算法的改进方面,提出了许多最大流问题的算法[9-16]。
针对Ford-Fulkerson算法存在标号的繁琐、增广链寻找的任意性和运行效率慢的缺陷,文中提出了一种基于宽度优先的网络最大流求解算法。该算法利用宽度优先搜索原理,寻找一条包含剩余容量最大的弧的最短增广链,且删除饱和弧后,运用了修复最短增广链的方法[17],简化了网络且避免了反复寻找新的增广链,达到了优化Ford-Fulkerson算法的目的。
1 基本概念
1.1 最大流的模型
定义1[6]:定义一个含容量的网络,记为G=(V,A,c),定义流fst为网络G=(V,A,c)中从始点s到终点t的流,如果fst满足下列条件:
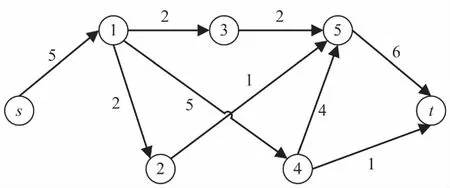
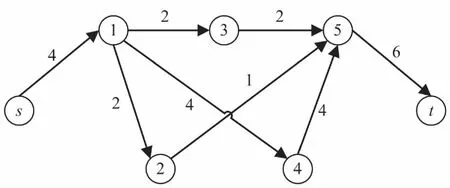
则fst是网络G的一个可行流。在所有满足条件的可行流中,流量最大的可行流被称为最大流,记作fmax。上式中满足f(i,j) 剩余网络[5-6](residual network)是指在一张含可行流的容量网络图中所有非饱和弧及所有节点的集合,亦可用反向弧在网络中标记出饱和弧及当前流。记剩余网络为U(f)=(V,A(f),c(f)),需满足两个关系: (1)∀(i,j)∈A(G),若f(i,j) (2)∀(i,j)∈A(G),若f(i,j)>0,则CU(j,i)=f(i,j)。 改进算法的主要思想是:找一条从始点vs到终点vt包含剩余容量最大的弧的最短增广链P,然后对其不断修复,减少重新寻找可增广链的执行次数。首先,在容量网络G=(V,A,c)中,取任意一个可行流f(一般取零流)。在容量网络G=(V,A,c)中,使用宽度优先原则,搜索一条从始点vs到终点vt包含剩余容量最大的弧的最短增广链P,然后在最短增广链P上删除饱和弧和调整相应弧的容量。进一步是增广链修复的过程,搜索满足条件的节点,找到一条包含删除弧两个端点的新的增广链。具体修复的过程是:取距离始点vs最近的删除弧(vs,vm)及距离终点vt最近的删除弧(vq,vn),得到断点为vs、vn,寻找包含vs到vn的一条路径,且修复的最短增广链包含剩余容量最大的弧,如图1所示。若找不到满足条件的节点,则意味着修复结束。在剩余容量网络中重新找一条包含剩余容量最大的弧的最短增广链,重复以上操作。若在剩余容量网络中,找不到从始点vs到终点vt包含剩余容量最大的弧的最短增广链时,则整个算法终止。 图1 增广链的修复过程 在容量网络G=(V,A,c)中,开始于任意一个可行流f(一般取零流),执行以下步骤: Step1:从始点vs出发,找一条从始点vs到终点vt包含剩余容量最大的弧的最短增广链P(宽度优先原则)。如果不存在,结束,f就是G的最大流; Step2:求出该最短增广链P上各弧容量的最小值δ。删除饱和弧,并在最短增广链P的各弧上减去δ; Step3:修复增广链P,转Step2,如果不能修复,则转Step1。 在新算法的操作过程中,删除包含剩余容量最大的弧的最短增广链上的饱和弧,对最大流的求解并没有影响。因为在以后执行算法的过程中,这条弧的容量不可能减少或增加[18],只是简化了重新寻找可增广链的过程,且在剩余容量网络修复过程中,避免了重复搜索相关的弧。设容量网络G=(V,A,c)有m条弧,每次增广后,至少删除一条饱和弧,则最多经过m次增广后,网络G=(V,A,c)中就不存在从始点vs到终点vt的可增广链,此时算法终止,即新算法不会陷入死循环。 在容量网络G=(V,A,c)中,设节点数为n,弧数为m。在Step1中执行一次宽度优先搜索的复杂度为O(m),且沿宽度优先搜索寻找包含剩余容量最大的弧的最短增广链P时,步数不超过O(n)。在执行Step2时,每次至少删除一条饱和弧,故最多执行m次寻找包含剩余容量最大的弧的最短增广链,所以新算法的时间复杂度为:O(mn2)+O(m2)=O(mn2)。 新算法在实际的操作过程中,降低了时间复杂度。由于寻找包含剩余容量最大的弧的最短增广链、删除饱和弧及修复增广链,都会减少下一步寻找包含剩余容量最大的弧的最短增广链的搜索次数。 例:如图2所示,求从始点vs到终点vt的网络最大流。其中每条弧旁的数字表示容量。 图2 容量网络G 解:(1)在容量网络G=(V,A,c)中,将初始可行流取为零流f; (2)从始点vs出发,找一条包含剩余容量最大的弧的最短增广链。选取最短增广链P=vsv2v4vt,δ=min{5,6,6}=5,将δ的值加到流值f上,得到新的可行流,仍记为f。删除饱和弧(vs,v2)及(v2,v4),并在最短增广链P的各弧上减去δ,如图3所示。 图3 删除饱和弧后的网络图 (3)修复最短增广链P,其中vs,v4为断点,修复可得P=vsv1v4vt为最短增广链,δ=min{5,5,1}=1,将δ的值加到流值f上,得到新的可行流,仍记为f。删除饱和弧(v4,vt),并在最短增广链P的各弧上减去δ,如图4所示。 图4 修复后删除饱和弧的网络图 (4)修复最短增广链P,其中v4,vt为断点,修复可得P=vsv1v4v5vt为最短增广链,δ=min{4,4,4,6}=4,将δ的值加到流值f上,得到新的可行流,仍记为f。删除饱和弧(vs,v1),(v1,v4)及(v4,v5),并在最短增广链P的各弧上减去δ。 (5)此时在容量网络G=(V,A,c)中,不存在从始点vs到终点vt的可增广链。于是可得图5所示的最大流f,流值为10。 图5 最大流f 注:用该算法只需一次寻找增广链,两次修复增广链。若用Ford-Fulkerson算法,则需要三次寻找增广链,两次修复增广链的过程才能得到最大流值10,过程复杂,空间占用大,运行时间长,这里就不给出详细的求解过程。 将该算法在MATLAB2012b软件中进行仿真实验。仿真实验所采用的随机网络是由BA无标度网络的方法随机生成的,仿真实验的网络规模设为500,1 000,1 500,2 000,2 500,3 000,3 500个节点,且针对给出的网络规模均进行五次仿真实验求平均值。在这样的仿真条件下,利用宽度优先原则对Ford-Fulkerson算法与文中算法进行平均运行时间的比较,如图6所示。 图6 平均运行时间的比较曲线 由图6可以得到,在对BA无标度网络进行最大流求解过程中,在相同的网络规模下,文中算法要比Ford-Fulkerson算法所用的运行时间短,这与之前的分析相吻合。 最大流问题是具有广泛应用的经典组合优化问题,文中是在Ford-Fulkerson算法的基础上,提出了一种基于宽度优先的网络最大流求解算法。该算法避免了标号的过程,并且借助宽度优先搜索原理、寻找包含剩余容量最大的弧的最短增广链、删除饱和弧及增广链修复的方法,把复杂的网络简单化,计算量也得到了降低,使整个算法的执行效率得以提高。通过数值实例验证了该算法的简便性、实用性,且仿真实验说明了该算法的运行速率要比Ford-Fulkerson算法快。1.2 剩余网络(增量网络)
2 一种改进的最大流算法
2.1 算法思想

2.2 算法步骤
2.3 算法可行性分析
2.4 算法复杂度分析
3 数值实例与分析


4 算法的仿真与比较

5 结束语
