基于混合算子蛙跳算法求解线性方程组

郭德龙 周锦程

（1.黔南民族师范学院 数学与统计学院，贵州 都匀 558000）（2.黔南民族师范学院 复杂系统与计算智能重点实验，贵州 都匀 558000）

0 引言

生产和实践中，求解线性方程组的问题是普遍存在的，例如潜艇、航空等方面很多问题的求解都可以转化成求解线性方程组的问题。 求解线性方程组的传统方法在遇到大型的线性方程组时难以驾驭，实用性不强；牛顿迭代法可以得到不错的计算结果，但依然存在一定的局限性，迭代时初值的选取要求十分严格，选取的初值欠好，可能会导致不收敛；其次，每一次迭代都要计算，计算量很大，

给应用带来很大的阻碍。 混合蛙跳算法 （SFLA）是Eusuff 和Lansey 在2003 年第一次提出的，是一种崭新的智能优化算法，它结合了PSO 和模因算法两者的所长，算法的参数较少、收敛的速度和计算速度较快、优良的全局搜索能力、便于实现等特点[1]。 当前，SFLA 广泛的应用在贴片机贴装顺序优化问题、 数值优化和组合优化、 函数优化控制器参数调整和聚类问题等很多的规模中[2]。 所以本文在基于SFLA 的基础上来求线性方程组的解，不改变原算法的子群内部搜索策略，将线性方程组转化成优化问题， 然后利用蛙跳算法求该优化问题从而求出线性方程组的解。

1 问题描述

线性方程组的一般形式如下：

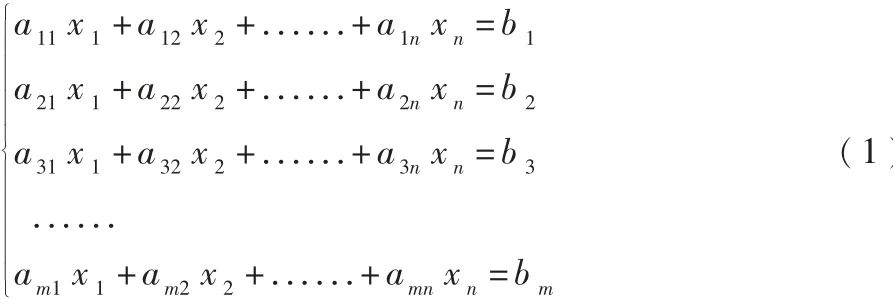
其中未知量列X=（x1，x2，L L xn）T，常数列b=（b1,b2,L L,bm）T，系数矩阵A=（aij）mn，求（1）的解。

1.1 问题转化

由（1）变形可得：

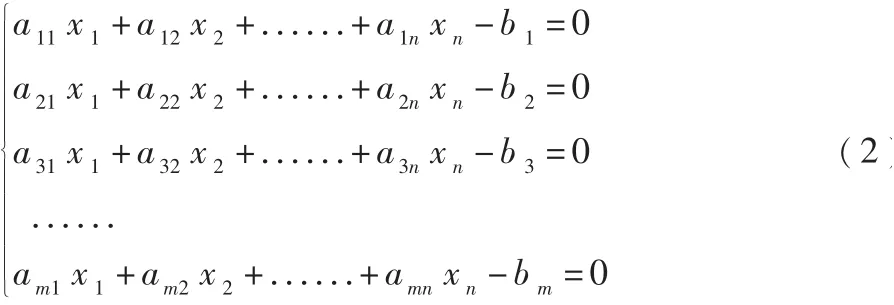
将（2）式化为：

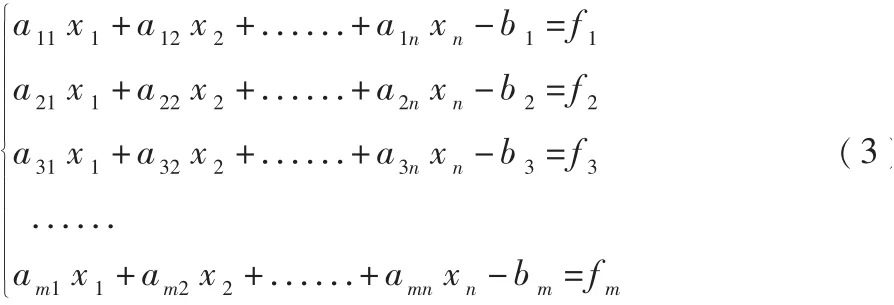
由（3）式中的方程组转化为如下函数形式：

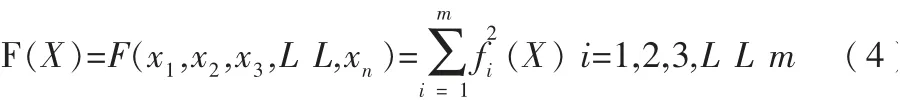
（1）、（4）可转为如下优化问题：

每一个未知数的解对应每一只青蛙，搜罗最好的青蛙过程就是在搜索最好的解的行程，然青蛙的好坏由优化模型的适应度函数决定。 构造的适应度函数如下:

所以求线性方程组（1）的解就转变成求函数Y 的最小值优化问题。

2 混合蛙跳算法

2.1 算法原理

SFLA 的执行过程就是模仿一群青蛙在有限空间的一块区域内觅食的过程，算法的性能良好。 青蛙跳跃觅食过程中，经过分组和重新排列，使青蛙之间进行信息交换，然后相互学习，搜罗出区域内食物最好的地方，并通过跳跃将自己的位置更新到食物较多的位置。 如下：

一、在一片水池中，每一个青蛙种群都是随机生成的，其中的青蛙无论是从构造上还是行为习惯上都是相同的，一只青蛙就是一个解。 一群青蛙通过自身的组织能力，将相同个数的青蛙进行组团搜罗，形成的每一个小团体即为子种群。

二、子群中的青蛙在更新到最好位置时，它们之间会进行信息交流，从而找到食物源最丰富的地方即问题的最优解。 青蛙种群中各个子种群的最优解又进行混合交流搜罗出最好的解。

三、SFLA 的局部搜索和混合交流是算法的核心，它们的结合使算法拥有了良好的搜罗能力，这也是其他群体智能优化算法的不足之一。 充分利用这优势向着池塘最优的方向进行搜索，直到找到最优解为止。

2.2 SFLA 的基本流程图

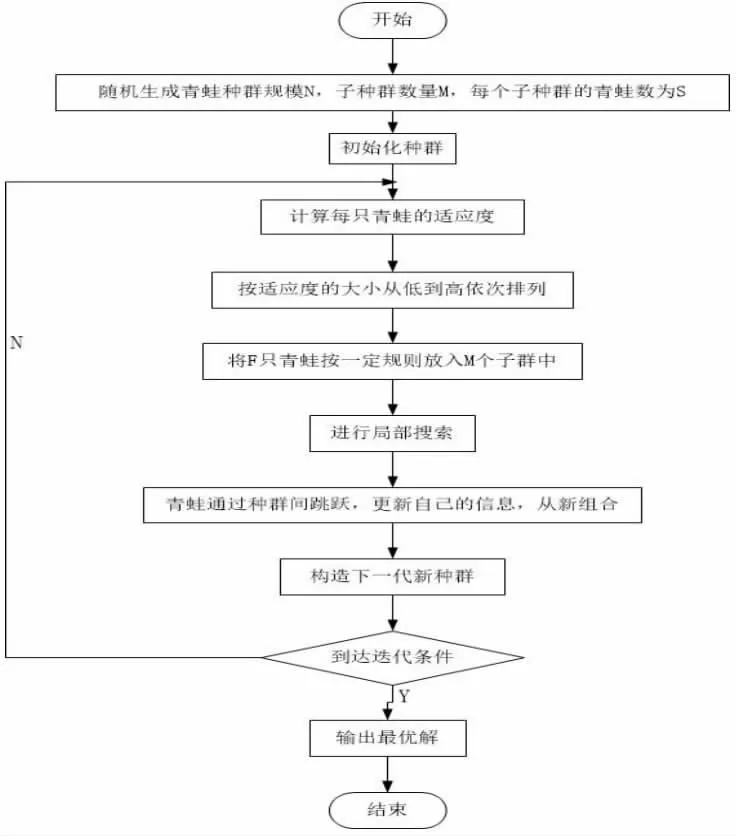
图1

3 SFLA 求解线性方程组

步骤1 种群初始化。 确定方程组中的未知数x 的个数为N 个； 第i 个未知数x 在D 维空间中对应的坐标是xi=（xi1,xi2,xi3,,L L,xiD）；

步骤2 把xi代入函数中，看它是否是使函数F（X）=或是使方程最接近于0 的解，即求出了函数的适应度fitness=F（X）；

步骤4 子种群的划分。 将N 按一定规则分成M个子种群 ｛Y1,Y2,Y3,L LYM｝，每一个子种群有S个解，其中N=M*S[3]。 分组规则如下：

第一个解分入Y1， 第二个解分入Y2， 第三个解分入Y3，直到第S 个解分入YM，然后再将第S+1 个解分入Y1，将第S+2 个解分入Y2，一直轮回分派直到所有的解N 都分派完为止。 分派完成后，找出各个子种群中适应度最好的解xa=（xa1,xa2,xa3,L L,xaD），适应度最差的解xb=（xb1,xb2,xb3,L L,xbD），种群中适应度最好的解为xw=（xw1,xw2,xw3,L L,xwD）[1]。

步骤5 子种群的局部搜索。 每次搜罗中，对子种群中最差的青蛙进行位置更新，按如下公式进行：

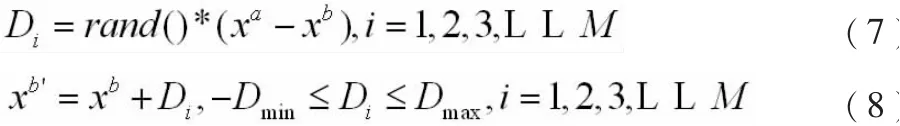
其中rand 是（0，1）间随机生成的数，Di是解的移动步长，Dmax表示青蛙最大移动的步长；按（7）式和（8）式进行每一次的局部搜索， 且对各个子种群的最差解xb进行位置更新这一操作。 按（7）式中计算出最差的解xb更新后的得到解xb'，若f（xb'）比f（xb)好，则就用xb'替代xb，若没有改进则用xw来代替xb。 再利用公式（7）（8）重新计算更新后的解，如果更新后的解比xb'更好，则用xb'替代最差的解xb，若仍然没有改进，则从搜索中从新随机产生一个新的解来替换原来的xw，子种群中最差的解的位置就得到了改变，各个子种群都重复上述搜索，一直到规定的最大局部搜索的次数为止[2]。

步骤6 子种群混合。 将求出的全部解混在一起，又重新划分子种群，再实施局部搜索，直到循环满足终止条件。

4 实验仿真结果与分析

4.1 仿真结果

实验环境Lenovo-PC 机Intel （R）Core （TM）i5-5257U CPU、2.70GHz、Window8、RAM:4GB 和MATLAB R2014a 中进行。为了测试该算法求解线性方程组的性能，任意选取了6 个线性方程组进行测试。 参数设置：组内迭代数Ne=25，最大步长smax=100，种群分组数m=50，每组青蛙数n=35，种群总进化代数MAXGEN=100， 优化问题维数d=25。

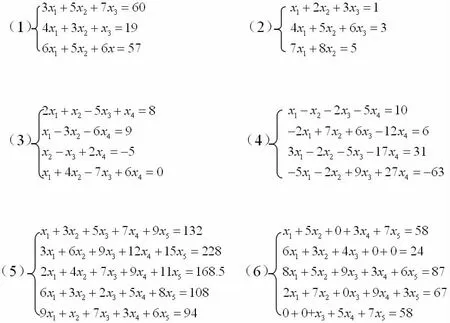
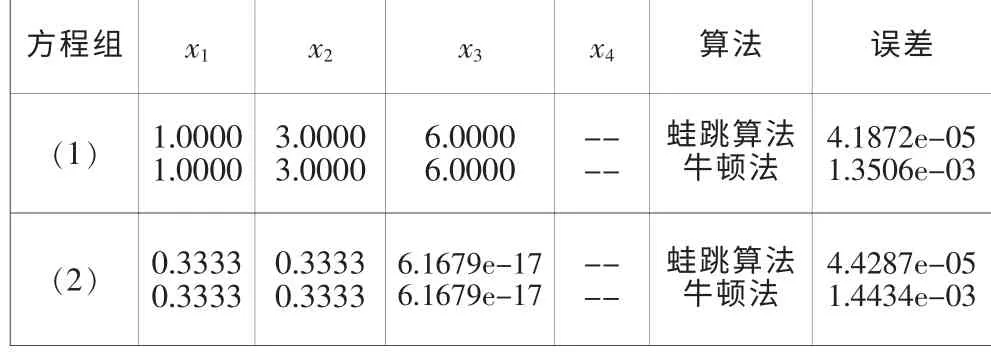
表1 线性方程组的求解结果

图2 第一个线性方程组的优化过程

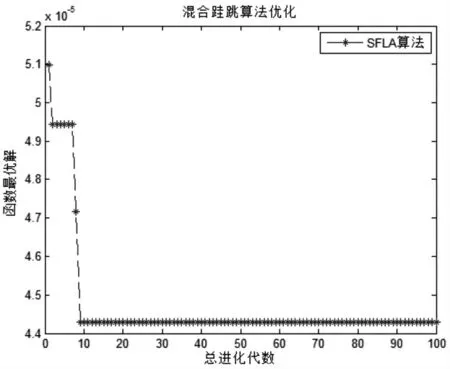
图3 第二个线性方程组的优化过程

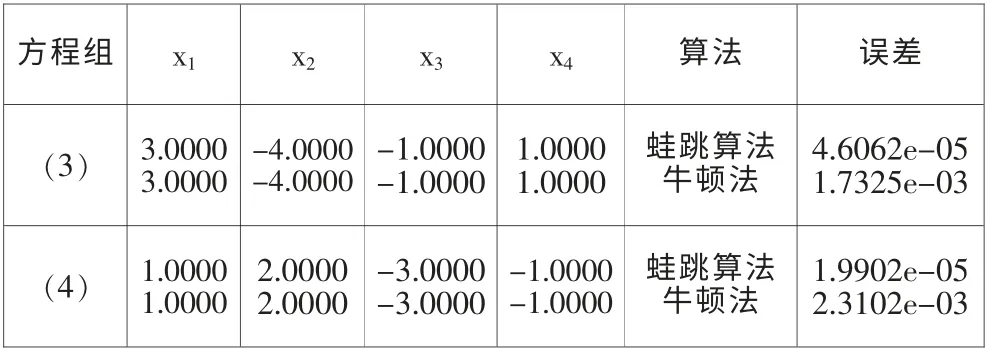
表2 线性方程组的求解结果

图4 第三个线性方程组的优化过程

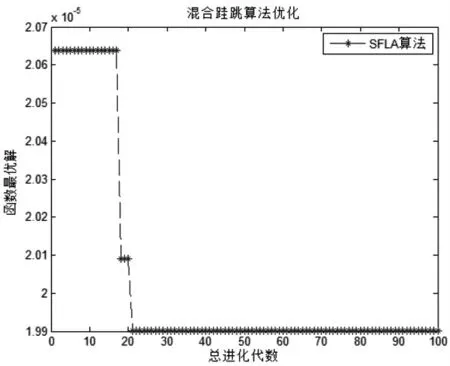
图5 第四个线性方程组的优化过程

表3 线性方程组的求解结果

图6 第一个线性方程组的优化过程

图7 第二个线性方程组的优化过程

4.2 结果分析

从图2-图7 中，可看出SFLA 求解线性方程组的解是可行的，且每次都能在较短时间内寻找到最优解。 从图中可看到SFLA 在求解精度上与传统方法相比提高了很多，收敛速度方面上的效果也比传统方法还要好， 跟牛顿迭代法相比，SFLA 的求解效果都较好； 也可以看到SFLA 对求解线性方程组的解也便于实现。

5 结束语

SFLA 算法的性能良好， 种群中的青蛙是有智能行为的， 在解决各类优化问题方面得以成功的应用。 基于这些优点， 将原线性方程组化成解优化函数问题，再利用SFLA 算法来求函数的优化问题， 间接求得方程组的解。 SFLA 算法不用考虑初值的选取，且参数算法少，搜索能力强，无论是简单函数还是复杂函数，都便于实现。 6 个例子仿真实验结果显示，该算法求解线性方程组的解比牛顿迭代法好，提高了解的收敛速度,同时也得到比传统方法还要好的求解精度。