干摩擦阻尼结构对失谐叶盘振动局部化的约束作用
2019-06-11刘雅琳刘硕上官博徐自力
刘雅琳 刘硕 上官博 徐自力
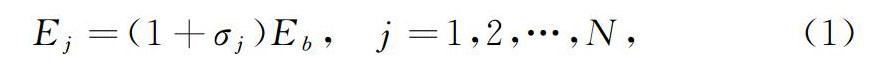
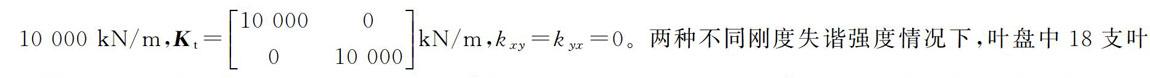
摘要:为了研究干摩擦阻尼结构对失谐叶盘系统振动局部化的影响,采用能够复现局部微动滑移特征的三维微滑移干摩擦模型和抗混叠时频域融合算法,对含干摩擦阻尼结构的失谐叶盘系统进行了强迫振动的计算模拟。比较了考虑围带处干摩擦阻尼和未考虑干摩擦阻尼时叶片振动响应的变化及局部化因子的大小,并研究了干摩擦阻尼参数在失谐叶盘系统减振控制中的影響规律。计算结果表明:干摩擦阻尼结构可降低失谐叶盘系统振动响应的局部化程度,叶片间的摩擦约束力完全不同,每支叶片所对应的最优初始正压力及最优摩擦系数均不相同。由于干摩擦阻尼结构对失谐叶盘中每支叶片的减振效果存在差异,在进行失谐叶盘系统减振设计时需考虑摩擦控制参数与各个叶片之间的匹配问题。
关键词:非线性振动力学;摩擦接触;叶盘;失谐; 振动控制
中图分类号:TK263.3文献标志码:A
LIU Yalin, LIU Shuo, SHANGGUAN Bo, et al.Effect of the dry friction damping structure on the localized vibration of mistuned bladed disk[J].Journal of Hebei University of Science and Technology,2019,40(1):1-8.Effect of the dry friction damping structure on the localized
vibration of mistuned bladed disk
LIU Yalin1, LIU Shuo1, SHANGGUAN Bo2, XU Zili3
(1. School of Environmental and Municipal Engineering, Xian University of Architecture and Technology, Xian, Shaanxi 710055, China; 2. Xian Thermal Power Research Institute Company Limited, Xian, Shaanxi 710054, China; 3. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xian Jiaotong University, Xian, Shaanxi 710049, China)
Abstract:In order to study the effect of the dry friction damping structure on the localized vibration of mistuned bladed disk, the forced vibration response of a mistuned bladed disk with dry friction damping structure is investigated by using three-dimension microslip friction contact model which could reproduce the characteristics of local micro-motion slip and anti-aliasing hybrid frequency-time domain method. The variation of blade vibration response and the change of localization factor are compared with considering dry friction damping at the blade shroud and not considering dry friction damping. And the influence of the dry friction damping parameters on the vibration control of mistuned bladed disk system is discussed. The results show that the dry friction damping structure can reduce the degree of localization of the vibration response of the mistuned bladed disk system, the friction force between the blades is completely different, and the optimal initial normal pressure and the optimal friction coefficient for each blade are different. Therefore, the effect of the dry friction damping structure to each blade of the mistuned bladed disk is different, and the vibration reduction design of the mistuned bladed disk needs to consider the matching relationship between control parameters and mistuned blade.
Keywords:nonlinear vibration mechanics; frictional contact; bladed disk; mistuned; vibration control
叶片-轮盘(叶盘)结构是透平机械的核心部件,也是工作环境最恶劣、结构最复杂、故障最多的部件。受加工误差、运行磨损以及材料性质差异等多种人为因素或随机因素的影响,叶盘中各扇区间的几何参数或物理性质不可避免地存在一定的偏差,从而造成叶盘系统的失谐。失谐叶盘结构的振动模态沿周向不再呈现周期对称性,部分叶片的模态振幅会远大于其他叶片,从而导致部分叶片的振动应力过大,降低叶片的疲劳寿命,引发叶片的高周疲劳失效[1-3]。
为减少叶片的高周疲劳失效、延长叶片服役寿命,采用干摩擦阻尼结构增加叶片的结构阻尼是目前较为普遍的方式[4-6]。然而,原本就复杂的叶片系统由于干摩擦阻尼结构的存在成为变刚度、变阻尼的非线性动力学系统,再加上失谐因素的影响,给含有干摩擦阻尼结构的失谐叶盘系统振动特性以及振动局部化抑制的研究增加了许多困难。已有许多学者对失谐叶盘的振动特性进行过研究[7-12],但从约束失谐所引起的局部化振动角度来研究干摩擦阻尼结构对失谐叶盘系统振动响应的影响却为数不多[13-17]。上述研究中,有的使用集中质量模型对失谐叶盘系统进行建模,有的使用一维摩擦运动模型对围带接触运动进行简化,有的使用一阶HBM对结果进行近似处理。大量的简化必然会造成许多重要动力学特性信息的丢失,这也是失谐叶盘研究并未取得较为一致研究结论的原因之一。开展干摩擦阻尼结构对失谐叶盘系统局部化振动影响的研究,可在叶盘系统的设计阶段通过引入抑制失谐局部化振动的方法来降低叶盘对失谐因素的敏感程度,进而提高汽轮机、燃气轮机等叶轮机械的安全可靠性。
河北科技大学学报2019年第1期刘雅琳,等:干摩擦阻尼结构对失谐叶盘振动局部化的约束作用本文将三维微滑移摩擦接触模型和抗混叠时频域融合算法应用到失谐叶盘系统中,研究了干摩擦阻尼结构对失谐叶盘系统振动响应的影响,并对重要的接触面摩擦参数在失谐叶盘减振控制中的影响规律进行了分析,其结论可为正确理解失谐叶盘系统的振动控制、设计含非线性干摩擦阻尼的叶盘系统提供理论参考。
1系统模型及运动方程
与协调系统不同,失谐叶盘系统必须采用整体有限元模型进行计算。为方便后续数值比较和分析,本文建立了一个包含18支叶片的模拟失谐叶盘系统,如图1所示。该有限元模型共包含72 943个节点和236 684个8节点6面体单元。系统的泊松比、杨氏弹性模量和叶片密度分别设置为ν=0.3,Eb=2.06×105 MPa和ρb=7.8×104 kg/m3。叶顶采用平行围带结构提供叶片间摩擦接触进而产生附加干摩擦力。
假定轮盘是周期对称的,使用叶片弹性模量的正态分布模拟叶片的刚度失谐[10]。叶片的弹性模量值可以表示为Ej=(1+σj)Eb,j=1,2,…,N,(1)式中:Ej,σj和Eb分别表示失谐叶盘中第j个叶片的弹性模量、失谐量及标准叶片的弹性模量。为不失一般性,从正态分布中随机选取样本作为弹性模量失谐的偏差量,将正态分布的标准差设为5%和10%, 平均值设为零。使用5%模拟因加工误差等因素产生的一般性偏差,使用10%模拟大失谐或故意失谐等极端条件下的误差[18]。
叶盘系统的整体运动方程可表示为M(t)+C(t)+Kx(t)=fl(t)+fnl(t,x,),(2)式中:M,K,C表示叶盘系统质量矩阵、刚度矩阵和材料阻尼矩阵;x(t)表示叶片位移向量;fl(t)为线性激振力向量,下标l为linear缩写;fnl(t,x,)表示围带处与叶片位移、速度相关的非线性干摩擦力向量,下标nl为nonlinear缩写。
2.1三维微滑移摩擦接触模型
在进行接触面运动描述时,采用了能够模拟围带接触面黏滞-滑移共存,以及接触面法向正压力分布不均匀状况的三维微滑移摩擦接触模型,如图2所示。与传统三维摩擦接触模型相比,该模型具有下述特点:1)将对应的围带接触面离散成多个子区域,在相对应的子区域间建立一组接触点对。每组接触点对都能够描述三维接触运动,且每组接触点对之间的接触运动状态是单独判断的,因此整个围带接触面上的摩擦作用力为各组接触点对的合力。2)可通过切向刚度矩阵考虑接触表面各向同性或各向异性的特征。3)可将接触点对在一个运动周期内离散成若干离散时间点,在每个时间点判断接触点对的运动状态,得到相对应的摩擦约束力。不需要像解析模型那样寻找接触点对运动状态转变的临界点,分段求解摩擦约束力。
以两接触面上任意一组接触点对为例,简要说明摩擦约束力的求解方法。假设某一摩擦接触点对(见图3)中包含两个摩擦节点,分别命名为节点A和节点B,两节点间存在无质量弹簧Kt(切向)和kn(法向)。将切向接触刚度定义为式(3)所示形式,以表征由于存在加工误差、材料非均匀、非正常工况运行磨损等因素所引起的各向异性。Kt=kxxkxy
kyxkyy 。(3)假设在整个摩擦接触过程中节点A与两接触面的面1始终保持黏滞,节点B沿面2做黏滞-滑移运动,以产生切向的摩擦约束力。当两接触面未发生振动时,节点A,B重合在一起。当两接触面发生相对运动时,由于假设A与面1黏滞,节点A的运动轨迹可由面1的运动得到,只需对节点B的运动状态进行分析就可以得到两接触面间的运动轨迹及摩擦力分布。若两接触点对之间的法向运动分量过大而导致节点B与面2发生分离,该节点的摩擦力按零对待。摩擦约束力的具体求解方法见文献\[19\]。
2.2抗混叠时频域融合算法
含干摩擦阻尼结构的失谐叶盘系统振动响应的求解不仅需要计算失谐叶盘中每支叶片的振动情况,还要计算叶片与叶片之间的非线性摩擦接触,因此如何高效且准确地求解其非线性动力学方程便成为叶片响应分析的关键问题。本文选取了融合时频域分析双重优势的抗混叠时频域融合算法[20]对失谐叶盘系统进行求解。对系统运动方程进行求解,首先需要对方程两边同时进行傅里叶变换,并引入可满足离散傅里叶变换需要的离散频率值ωk。X(ω)代表位移向量x(t)经傅里叶变换后的频域形式;Fl(ω)代表激振力fl(t)經傅里叶变换后的频域形式;Fnl(ω,X(ω))代表非线性摩擦力fnl(t,x,)经傅里叶变换后的频域形式。如此,可得到下述非线性代数方程组H(ω)·X(ω)=Fl(ω)+Fnl(ω,X(ω)),(4)
H(ω)=-(kω)2M+ikωC+K,(5)
ω={ωk},ωk=2πkΔt·Nk,k=0,1,…,Nk-1,(6)
式中:H(ω)为系统的动刚度矩阵,与频率ω相关;Δt和Nk分别代表离散傅里叶变换所涉及到的采样时间及采样点数。由于式(4)是未知量X(ω)的非线性代数方程组,因此需要迭代求解。图4给出了抗混叠时频域融合算法的计算思路。图4中,符号Nk表示频域的谐波采样数;Nt表示时域内的离散点数目;上标i表示第i次迭代值;下标j表示第j个摩擦接触点。
计算开始于某个给定的频域振动响应初值X(0)(ωk)或者第i次迭代值X(i)(ωk),选取第j个位于摩擦接触界面上的自由度X(i)j(ωk),通过快速抗混叠傅里叶变换(FAFT)的逆变换,得到第j个摩擦接触界面上自由度在时域上的振动响应x(i)j,t,然后通过对接触面的摩擦接触行为进行模拟,得到时域上的摩擦约束力f(i)nl j,t(t,x(i)(t))。通过FAFT变换,得到频域上第j个摩擦接触界面上自由度的摩擦约束力F(i)nl j,重复计算所有摩擦接触点的摩擦约束力,得到F(i)nl。在F(i)nl确定的情况下,可以计算下一迭代步接触界面上自由度在频域上的振动响应X(i+1)(ωk)。这样就完成了一个迭代子步,重复这个迭代过程,直到满足计算精度要求为止。
3干摩擦阻尼结构对失谐叶盘系统振动局部化的影响
3.1振动响应
因受非旋转部件与旋转部件的扰动,气流会在叶片上形成周期性的激振力载荷,通过谐波分析可将此激振力表示为若干谐波分量的叠加。由于实际运行过程中,每个机组、每一级叶盘所受的激振力都不相同,本文通过在每支叶片顶部施加正弦激励对激振力形式进行模拟。假设叶盘中第j支叶片所受的激励为Fxj(t)=100 sin(ωt+jφr),
Fyj(t)=100 sin(ωt+jφr),
Fzj(t)=100 sin(ωt+jφr),(7)式中:ω代表激励频率;φr=2πr/N代表相邻叶片所受激励的相位差,r为激励阶次,N为叶片数。
在相邻叶片围带接触面上建立接触点对,采用三维微滑移摩擦接触模型计算相邻围带接触面间的摩擦约束力。接触面干摩擦参数:初始正压力n0=20 N,摩擦系数μ=03,法向刚度和切向刚度分别为kn=10 000 kN/m,Kt=10 0000
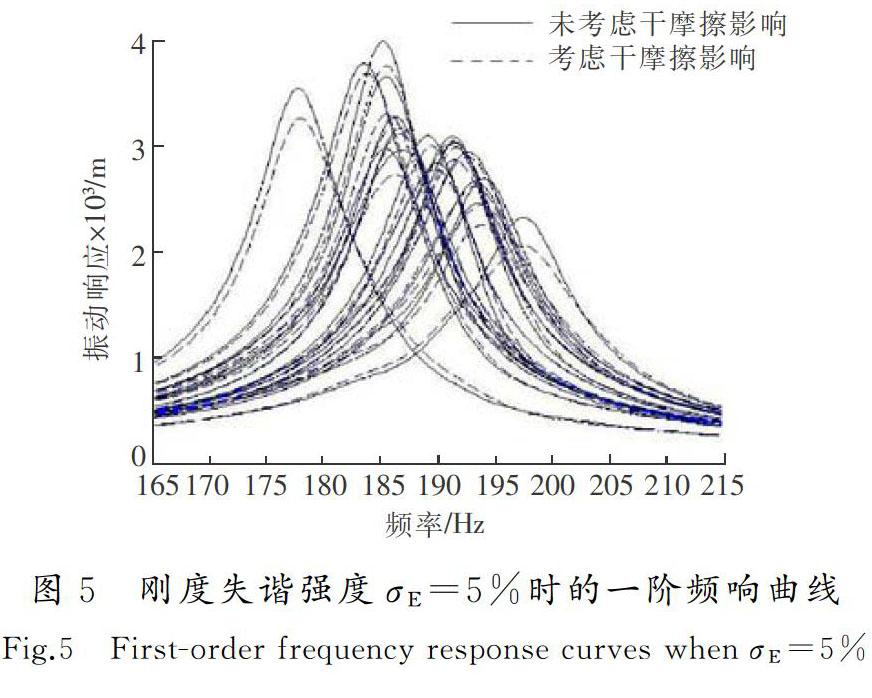
010 000kN/m,kxy=kyx=0。两种不同刚度失谐强度情况下,叶盘中18支叶片在一阶固有频率附近区域内的幅频响应曲线如图5、图6所示。图中,横坐标为激振力频率,纵坐标为3个方向的合成振幅。
未考虑围带阻尼时,由于“失谐”的影响,每支叶片的振动振幅和频率都存在差异。当刚度失谐强度σE=5%时,18支叶片中共振振幅最大为4.004 mm,最小为2.331 mm。刚度失谐强度σE=10%时,最大共振振幅为4.263 mm,最小共振振幅为2.240 mm。由于叶片的振动能量与振动位移相关,在同一叶盘中,叶片的振动位移不同,必然会导致振动能量分布不均,局部化振动突出。
考虑围带阻尼作用后,每支叶片的振幅都有所改变。刚度失谐强度σE=5%时,叶片非线性响应的最大共振振幅为3.769 mm,最小共振振幅为2.063 mm,与线性响应的振幅相比,最大降幅为11.483%,平均降幅为4.684%。刚度失谐强度σE=10%时,共振振幅最大为3.946 mm,最小为1.966 mm,与线性响应的振幅相比,最大降幅为12.879%,平均降幅为6.967%。由上述数据可见,在失谐叶盘中干摩擦阻尼结构仍然能够对共振幅值起约束作用,且对失谐量大的系统更为明显。
3.2局部化因子
为了明确摩擦阻尼结构对失谐叶盘系统振动局部化的影响规律,引入局部化因子,定量地对叶盘能量集中的程度进行描述。本文用失谐叶盘中叶片的最大振动位移与其他叶片的平均振动位移的差值来定义局部化因子L,其表达式[10]为L=A2max-1N-1∑Ni=1,i≠jA2i1N-1∑Ni=1,i≠jA2i,(8)式中:N为叶片数目;Ai为叶盘中第i支叶片的响应振幅;Amax为叶盘中最大的响应振幅;j为叶盘中最大响应振幅所对应的叶片编号。通过局部化因子可以描述叶盘中最大的叶片振动能量与其他叶片的平均振动能量之间的差异。
运用振动响应局部化因子分别计算自由失谐叶盘系统和干摩擦阻尼结构的失谐叶盘系统的振动响应局部化程度,结果如表1所示。
由表1可知,因围带相互接触而产生的干摩擦力使得系统的局部化因子数值下降(分别下降4.28%和447%),这表明干摩擦阻尼结构在一定程度上可改善失谐叶盘系统的振动局部化问题,且对大失谐量同样有效。
3.3接触面非线性摩擦力
以刚度失谐强度σE=10%时的叶盘为例,随机选取该叶盘上的3支叶片绘制了围带接触界面上x,y方向摩擦力的迟滞回线以及摩擦力在一个运动周期上的分布曲线,如图7所示。
由图7不难看出,x方向和y方向的摩擦力迟滞回线的形状和大小存在差异。由于摩擦力迟滞回线的面积代表干摩擦阻尼结构消耗叶片振动能量的大小,因此,干摩擦阻尼结构对失谐叶盘中每支叶片的减振效果存在差异。
4干摩擦阻尼参数对失谐叶盘系统的影响
振动过程中影响接触面相对运动和接触面接触状态转换的因素有很多,本文主要以接触面初始正压力和摩擦系数为例,分析其对含干摩擦阻尼结构失谐叶盘系统的振动特性的影响规律。
4.1接触面初始正压力对振动响应的影响
围带叶片在工作过程中,围带间的预紧力和转动时预扭叶片产生的扭转恢复力使得围带之间产生一定的压力,该压力直接影响叶片振動过程中摩擦接触面之间接触状态的转换,对研究干摩擦阻尼结构减振具有重要的意义。以刚度失谐强度σE=10%为例分析接触面初始正压力对失谐叶盘振动响应的影响规律。在不同的初始正压力下,叶盘上某3支叶片在一阶固有频率附近的幅频响应曲线如图8所示。所选取的3支叶片分别是图6中共振响应幅值最大的叶片(叶片1)、共振响应幅值最小的叶片(叶片2) 以及考虑非线性摩擦力之后与线性情况相比降幅最大的叶片(叶片3)。
图8中的3幅图变化趋势相似,随着接触面初始正压力的增大,共振频率一直增大,共振幅值先减小后增大,在变化的过程中都存在一个最优值使振动响应最小,但最优初始正压力的值却不相同。对应某一相同的初始正压力值,如n0=30 N,叶片1的减振效果好,而叶片2和叶片3却没有达到最佳减振效果,可见从控制的角度出发,使用完全一致的参数设计并不能使整个叶盘的运行效果达到最佳。因此,在进行失谐叶盘的减振设计时需要考虑叶片控制参数与叶片自身振动情况的相互匹配问题,即寻求每支叶片的最优控制参数,使整个系统的控制效果达到最佳。
4.2接触面摩擦系数对振动响应的影响
摩擦接触面所能提供的最大摩擦力取决于摩擦系数和法向正压力的大小,因此不同的摩擦系数将影响接触状态发生改变时的临界条件,进而影响接触摩擦力的大小,最终影响干摩擦阻尼的减振效果。以刚度失谐强度σE=10%为例分析接触面摩擦系数对失谐叶盘振动响应的影响规律。图9为不同接触面摩擦系数条件下叶盘上某3支叶片在一阶固有频率附近的响应曲线。
图9 a)中,摩擦系数从0.2增加到0.4,振幅从4.022 mm减小到3.880 mm,降幅为3.531%。图 9 b)中,摩擦系数0.2增加到0.4,振幅从2.045 mm减小到1.901 mm,降幅为7.041%。图9 c)中振幅下降不明显。3幅图中的共振频率都明显增大。可以看出,摩擦系数对系统共振频率和振动幅值都有影响,摩擦系数越大减振效果越好。对失谐叶盘系统而言,摩擦系数对每支叶片振幅的影响也不相同。
5结论
使用抗混叠时频域融合算法和三维微滑移摩擦接触模型对失谐叶盘系统的振动响应进行了研究,并对重要的接触面摩擦参数在失谐叶盘减振控制中的影响规律进行了分析,结果显示:
1)在计算中考虑干摩擦阻尼结构所产生的摩擦约束力后,叶片共振幅值下降,共振频率增加;摩擦约束力可降低失谐叶盘系统振动响应的局部化程度,对一般失谐和大失谐同样适用;
2)由于失谐叶盘各叶片间的摩擦约束力不同,使得每支叶片的减振程度有所差异;使用完全一致的参数设计并不能使整个叶盘的运行效果达到最佳,对失谐叶盘系统进行摩擦减振优化设计时需充分考虑每支叶片的振动差异及控制参数的匹配问题,即寻求每支叶片的最佳控制参数,从而使整个叶盘的振动最小。
本文仅研究了刚度失谐这一种失谐形式下叶盘的振动特性,并未涉及其他失谐形式及其耦合,摩擦接触的形式亦比较单一,后续可进行多种摩擦接触形式共同作用下的失谐叶盘控制研究,通过不断丰富研究结论,为正确理解失谐叶盘系统的振动控制、设计含非线性干摩擦阻尼的叶盘系统提供理论支撑。
参考文献/References:
[1]高阳,姚建尧,杨诚,等. 小失谐对整体叶盘结构动态特性的影响[J]. 航空动力学报, 2018, 33(7):1566-1574.
GAO Yang, YAO Jianyao, YANG Cheng, et al. Influences of small mistuning on dynamics characteristics of bladed disks[J]. Journal of Aerospace Power, 2018, 33(7):1566-1574.
[2]王建軍, 李其汉, 朱梓根. 失谐叶片-轮盘结构系统振动局部化问题的研究进展[J].力学进展, 2000, 30(4): 517-528.
WANG Jianjun, LI Qihan, ZHU Zigen. Vibratory localization of mistuned bladed disk assembles: A review[J]. Advances in Mechanics, 2000, 30(4):517-528.
[3]TANG W, BAEK S, EPUREANU B I. Reduced-order models for blisks with small and large mistuning and friction dampers[J]. Journal of Engineering for Gas Turbines and Power, 2017, 139(1): 012507.
[4]PETROV E P, EWINS D J. Advanced modeling of under platform friction dampers for analysis of bladed disk vibration[J]. Journal of Turbomachinery, 2007, 129: 143-150.
[5]JARELAND M H, CSABA G. Friction damper mistuning of a bladed disk and optimization with respect to work[C]// ASME Turbo Expo 2000: Power for Land, Sea, and Air. Munich:[s.n.], 2000: V004T03A009.
[6] 徐自力, 常东锋, 刘雅琳. 基于微滑移解析模型的干摩擦阻尼叶片稳态响应分析[J]. 振动工程学报, 2008, 21(5): 505-510.
XU Zili, CHANG Dongfeng, LIU Yalin. Forced response analysis of blade system with dry friction damper using one-bar microslip analytic model[J]. Journal of Vibration Engineering, 2008, 21(5): 505-510.
[7]LIN C C, MIGNOLET M P. An adaptive perturbation scheme for the analysis of mistuned bladed disks[J]. Journal of Engineering for Gas Turbines and Power, 1997, 119: 153-160.
[8]GRIFFIN J H, SINHA A. The interaction between mistuning and friction in the forced response of bladed disk assemblies[J]. Journal of Engineering for Gas Turbines and Power, 1985, 107: 205-211.
[9]PETROV E P. A method for forced response analysis of mistuned bladed disks with aerodynamic effects included[J]. Journal of Engineering for Gas Turbines and Power, 2010, 132(6): 1-10.
[10]王红建. 复杂耦合失谐叶片-轮盘系统振动局部化问题研究[D]. 西安: 西北工业大学, 2006.
WANG Hongjian. Investigation of the Vibration Localization Problem of the Mistuned Bladed Disk with Complicated Coupling[D]. Xian: Northwestern Polytechnical University, 2006.
[11]CASTANIER M P, PIERRE C. Consideration on the benefits of intentional blade mistuning for the forced response of turbomachinery rotors[J].Proceeding of the ASME Division,1997,55:419-425.
[12]HOHL A, WALLASCHEK J. A method to reduce the energy localization in mistuned bladed disks by application-specific blade pattern arrangement[J]. Journal of Engineering for Gas Turbines and Power-transactions of The ASME, 2015, 138 (9): 092502.
[13]CHA D, SINHA A. Statistics of response of a mistuned and frictionally damped bladed disk assembly subjected to white noise and narrow band excitations[J]. Probabilistic Engineering Mechanics, 2006, 21: 384-396.
[14]高峰,孫伟. 失谐整体叶盘的硬涂层减振研究[J]. 东北大学学报(自然科学版), 2018, 39(6), 856-861.
GAO Feng, SUN Wei. On the vibration reduction of mistuned blisks by hard coating[J].Journal of Northeastern University(Nataral Science), 2018, 39(6): 856-861.
[15]PETROV E P, EWINS D J. Method for analysis of nonlinear multiharmonic vibrations of mistuned bladed disks with seatter of contact interface characteristics[J]. ASME Journal of Turbomachinary, 2005, 127:128-136.
[16]JOANNIN C, CHOUVION B, THOUVEREZ F, et al. Nonlinear modal analysis of mistuned periodic structures subjected to dry friction[J]. Journal of Engineering for Gas Turbines and Power, 2016, 138(7): 072504.
[17]刘雅琳, 上官博, 徐自力. 干摩擦阻尼对失谐叶盘受迫振动的影响[J].西安交通大学学报, 2016,50(2):111-117.
LIU Yalin, SHANGGUAN Bo, XU Zili. Effects of the dry friction damping on forced vibration response of mistuned bladed disk [J]. Journal of Xian Jiaotong University, 2016,50(2):111-117.
[18]NIKOLIC M, PETROV E P, EWINS D J. Robust strategies for forced response reduction of bladed disks based on large mistuning concept [J]. Journal of Engineering for Gas Turbines and Power, 2008, 130: 022501.
[19]谷伟伟, 徐自力.干摩擦阻尼叶片的界面约束力描述及振动响应求解[J]. 振动工程学报, 2012, 25(1): 64-67.
GU Weiwei, XU Zili. Description of constraint force and prediction of vibration responses for dry friction damped blade[J]. Journal of Vibration Engineering, 2012, 25(1): 64-67.
[20]LIU Yalin, SHANGGUAN Bo, XU Zili. Improved hybrid frequency-time domain method for nonlinear analysis of frictionally damped blade systems[C]// American Society of Mechanical Engineers. [S.l.]:[s.n.], 2016: V07AT32A013-V007AT032A013
