画室里的数学证明

林革

达·芬奇是意大利最著名的艺术大师。这位“欧洲文艺复兴时期最完美的代表” 学识渊博、多才多艺，其代表作《蒙娜丽莎》《最后的晚餐》享誉全世界。达·芬奇不仅在绘画领域有着高超精湛的艺术造诣，在科学领域也展露出卓越的才能，被称为“艺术家里的数学家”，其研究成果和发明创造曾得到科学大师爱因斯坦的高度赞赏，因此被誉为“人类历史上绝无仅有的全才”。

有一天，达·芬奇来画室检查学生临摹《蒙娜丽莎》的情况，令他惊讶的是，竟然有半数的学生并没有潜心于作画，而在琢磨探讨“毕达哥拉斯定理”的证明。这个大家耳熟能详的定理，在我国古代也曾被研究证明过，并称为“勾股定理”：直角三角形两条直角边a、b的平方和等于斜边c的平方，即a2+b2=c2。有关这个定理的证明方法多种多样，不拘一格，因此也一直吸引爱好者尝试另辟蹊径。

学养深厚的达·芬奇自然知晓“毕达哥拉斯定理”的出处和背景，加上他对数学的酷爱，所以他并没有责备弟子，而是自己也饶有兴致地加入其中。于是，师生融洽和谐、自由开放的研究氛围很快就孕育出成功的“果实”。

达·芬奇的一位学生首先展示出自己的思路，具体分析如下：

图1和图2是两个形状、大小完全一样的正方形，边长为a+b，只是分割方法不同而已。可以看出，圖1的分割把正方形分成两个较小的正方形和两个完全一样的长方形，较小的正方形边长分别是a、b，即面积分别是a2和b2;两个完全一样的长方形面积都是ab，所以原正方形的面积S=a2+b2+2ab。图2的分割，则是把正方形分成1个较小的正方形和4个完全一样的直角三角形，较小的正方形边长为c，即面积为c2;4个完全一样的直角三角形的面积都是[12]ab，所以原正方形的面积S=c2+4×[12]ab=c2+2ab。

既然图1和图2的形状、大小完全一样，面积自然相等，则有a2+b2+2ab=c2+2ab，也就是a2+b2=c2。

就在弟子们议论纷纷之际，他们的导师达·芬奇已经惬意而轻松地挥着画纸宣布，自己也已顺利证明了“毕达哥拉斯定理”，大家顿时屏息静气，细听究竟。

达·芬奇的证明也是画图转化。具体方式是：先将边长分别为a、b的2个正方形和边长都是a、b、c的2个直角三角形拼合成图3，且画出整个图形的对称轴（图中虚线）;接着，将拼合成的图形整体从画纸中移出。再将取出的图形沿对称轴剪开，保留图形的左边，并将右边按照垂直方向翻转一周后重新拼合成图4;最后，将图4中一些顶点相连成一个c为边长的正方形和2个边长为a、b的直角三角形（图5），就完成了定理的证明。

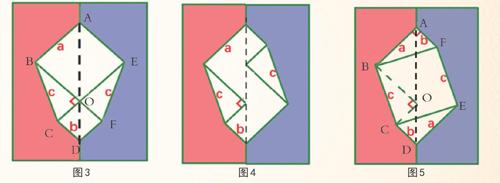
这种“美术证法”的正确性，可以通过并不复杂的数学分析来说明：⑴考虑到图3的对称性，直角A和直角D都被均分，因此翻转后的图5中，角A和角D仍是直角，所以可判断BF和CE是直角三角形的斜边c，而BC和EF也是c;⑵在图3中，∠ABO=90°，这个特征保持到图5中，即∠ABF+∠FBO=90°，因为直角三角形ABF和CBO完全一样，所以∠ABF=∠CBO，则∠CBO+∠FBO =∠CBF=90°，这表明BC⊥BF。由此可知，四边形BCEF是边长为c的正方形。

这样一来，图3中的图形面积为S=a2+b2+[12]ab+[12]ab=a2+b2+ab，剪拼而成的图5中图形面积为S=c2+ab，显然有a2+b2+ab=c2+ab，可得a2+b2=c2。

听完达·芬奇的分析后，画室里顿时爆发出热烈的掌声，恍然大悟的弟子们都被导师的奇思妙想深深折服，由衷钦佩。

通过对照比较可以发现，弟子的图解似乎更为简洁直观、通俗易懂，表面上应该比他的导师更胜一筹，但所谓外行看热闹，内行看门道，达·芬奇的证明其实更能体现数学的特性与奥妙，内蕴暗伏的构造、割补、对称、旋转、转化等数学思想，更加体现出艺术大师非同凡响的数学智慧，大家也可以从其“数形结合”的内涵中，感受到绘画与数学碰撞出的奇妙火花。