多频正弦信号峰值因子最小化方法研究

宿常鹏 王雪梅 许哲 李骏霄 邱洪彬

摘要：为有效解决频率特性测试中多频正弦激励信号的峰值因子最小化问题，基于Schroeder相位编码准则，针对均匀功率谱信号，从相位修正的角度出发，提出一种基于自适应遗传算法的相位修正方法;针对非均匀功率谱信号，从功率调制的角度出发，采用代数方法推导出一种正弦调制的调制通式。通过Matlab进行数值仿真，与采用Schroeder相位编码方法计算的结果进行比较，实验表明：两种方法均能使信号的峰值因子平均降低0.2，且使信号的峰值因子保持在2以内，更适合作为频率特性测试的激励信号，其中添加修正项的均匀功率谱信号更适合大频带测试，而应用正弦调制的非均匀功率谱信号更适合小频带测试。

关键词：峰值因子;自适应遗传算法;相位编码;功率调制

中图分类号：TP206.1文献标志码：A 文章编号：1674-5124（2019）04-0016-05

0引言

在测量线性系统的频率响应或传递函数时，使用高信噪比的信号进行测试是非常重要的。一般通过增加信号的能量提高其信噪比，但是，为避免被测系统工作于非线性状态，输人信号的幅值是有限制的。此外，为激发被测系统的所有模态，输入信号必须包含足够的频率分量。所以如何在给定的幅值约束下增加信号的能量或者在给定的能量约束下减少信号的幅值，即信号峰值因子最小化问题，常见于雷达、声呐、通信技术、语音合成和测试信号的设计等领域。峰值因子问题至今仍无法有效解决，除非频谱分量的数量足够小以允许对所有相位角的组合进行穷尽搜索。

目前，虽然未发现使信号的峰值因子在全局最优的解析解，但已提出各种能够有效降低信号峰值因子的算法。如文献[1]基于woodward定理提出多频正弦信号的相位编码准则，其对于均匀功率谱（即各次谐波的幅值相等）的多频正弦信号效果很好，但对于非均匀功率谱的多频正弦信号效果不如随机相位编码的效果好。文献[2]提出一种基于标准遗传算法的相位搜索方法，该方法通过并行搜索相位空间中的局部最优解以降低多频正弦信号的峰值因子，但计算量大导致算法的计算时间长。文献[3]研究了一种利用互补自相关函数矩阵构造多相互补码对的方法，并提出利用多相互补码构成多频正弦信号的方法降低信号峰值因子，但由于利用互补自相关函数矩阵构造多相互补码对的求解过程复杂，且与参数的初始值有关，因此需要以不同的初始条件重复多次获得更好的结果。

本文基于schroeder提出的相位编码准则，从均匀功率谱和非均匀功率谱两个方面进行了改进，即对均匀功率谱信号的相位提出了一种基于自适应遗传算法的相位修正方法，对非均匀功率谱信号的功率给出了二次正弦调制的调制通式。

1基本概念

多频正弦信号为周期性信号，它是一系列离散频率的正弦信号的总和。目前，多频正弦信号主要应用于线性系统频率特性的快速测试，其数学表达式为

一般认为，方波信号由于存在突变使得测试过程极不平稳，故不适合用于系统频率特性的测试。而正弦信号的峰值因子为讵，是频率特性测试最理想的输入信号。故选择合理的相位叠加方式生成多频正弦信号的峰值因子越接近讵，该信号就越适合作为系统频率特性测试的输入信号。

2多谐差相信号概述

多谐差相信号是一种特殊的多频正弦信号，目前广泛应用于线性系统频率特性测试中。它由若干个功率、周期和初相有一定关系的余弦波叠加而成的周期性多频信号，通过调整组成信号的各正（余）弦分量的初相来形成自己特性，其表达式为

多谐差相信号为周期信号，做快速傅里叶变换时可以整周截断，避免谱泄漏。而且信号的频谱是离散的，可以抑制大部分的噪声干扰。同时正弦波叠加信号易于通过计算机或板卡产生，对硬件要求低。测试过程中，通过改变基波周期T和谐波数N改变测试频带，可以实现对任意频率点模态的激活，以满足不同系统测试的需要。

根据多谐差相信号的数学表达式和峰值因子计算公式，降低其峰值因子的方法主要有两种：1）在均匀功率谱信号的相位编码中添加修正项;2）对谐波功率进行调制产生非均匀功率谱信号。

3多谐差相信号峰值因子最小化方法

3.1峰值因子与信号总功率无关

由于均匀功率谱信号可以看作是非均匀功率谱信号的特例，故以非均匀功率谱的多谐差相信号为例进行说明。

由此可以得出结论，在各次谐波的相对功率保持不变的条件下，多谐差相信号的总功率不改变信号的峰值因子，该结论对于均匀功率谱信号同样成立。因此，对于多谐差相信号的峰值因子最小化问题可仅研究总功率为1时的情况。

3.2均匀功率谱信号峰值因子最小化问题

由均匀功率谱的多谐差相信号表达式可知，信号的峰值因子与总功率P无关，只与谐波数Ⅳ和基波周期T有关。由于N和T决定了测试频带，可根据实际被测系统确定，当N、T确定时，信号的峰值因子也随之确定。

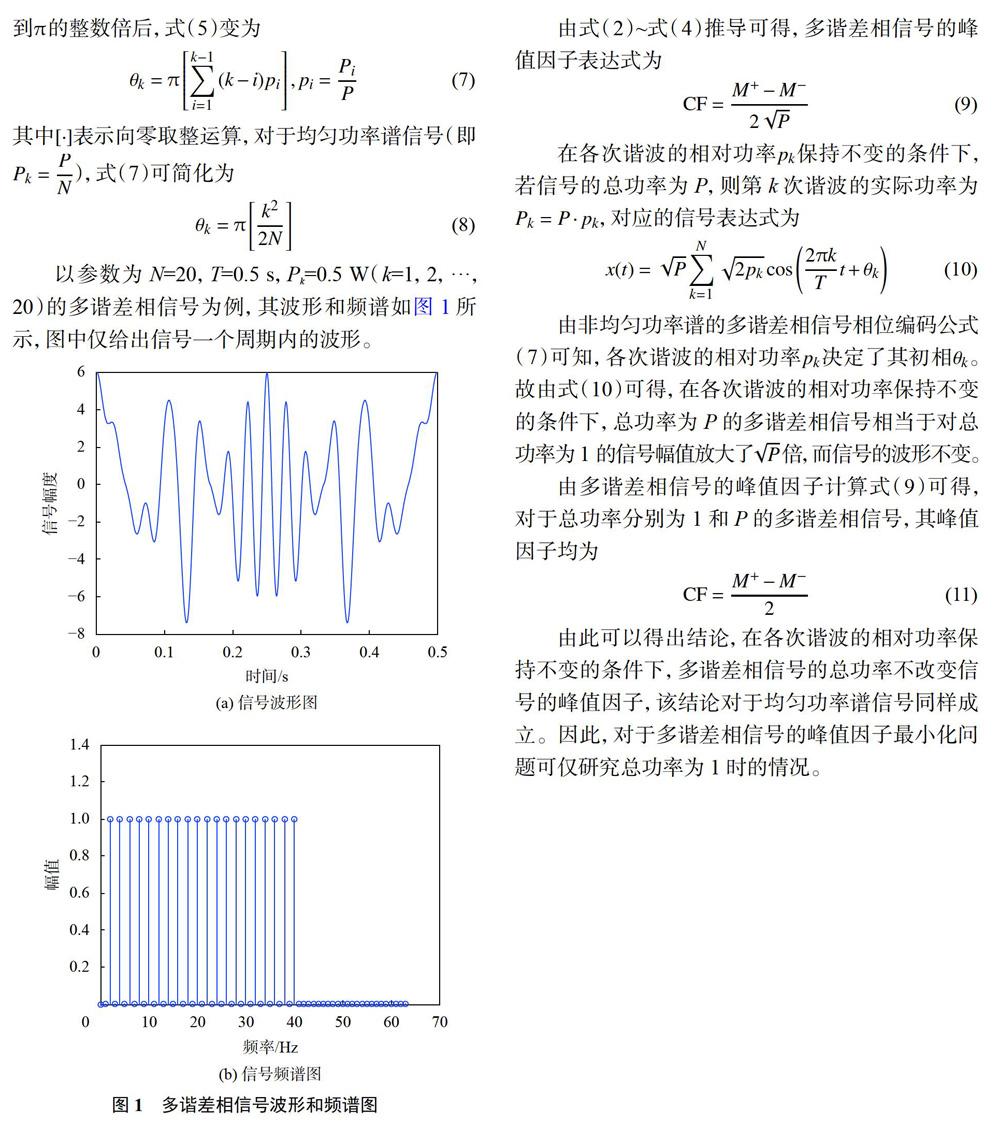
schroeder M.R在文献[1]中提出，对具有均匀功率谱的多谐差相信号，如果改变个别谐波的初相将得到更低的峰值因子，并给出了具体的例子。因

4实验分析

多谐差相信号常用于伺服机构的频率特性测试，而伺服機构频率测试的范围一般为0.1～100Hz，其核心工作频带为0.1～20Hz。根据Nyquist定理，采样频率必须大于被测信号最高频率的两倍。工程上采样频率一般按照上限频率的10～50倍确定。另外考虑到采样点数量过大会急剧增加数据存储和处理的难度，故常采用分段采样的方法减少采样点数。因此，实验中将测试频带分为大频带100Hz和小频带20Hz，由此确定谐波数Ⅳ、基波周期T的数值。同时设置总功率P=1w，采样频率1kHz，即采样时间T4=0.001s。

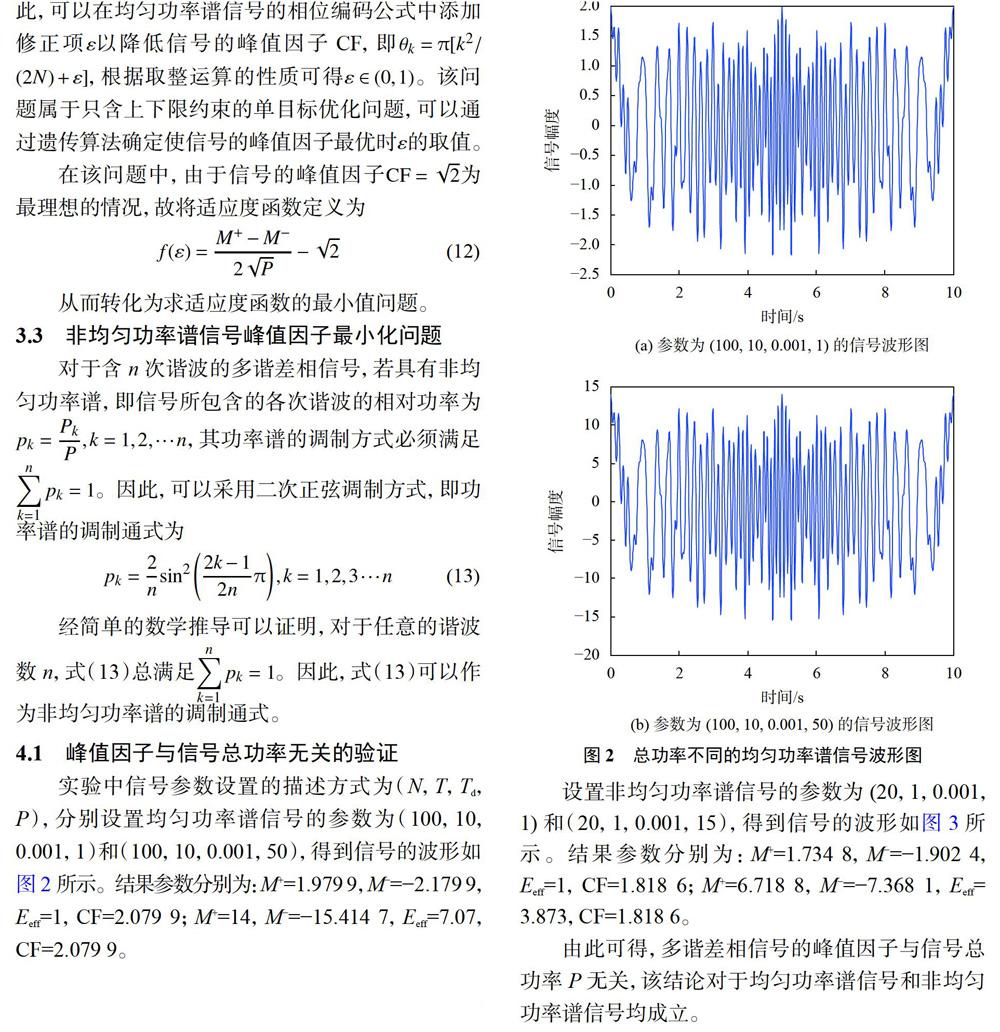
由此可得，多谐差相信号的峰值因子与信号总功率P无关，该结论对于均匀功率谱信号和非均匀功率谱信号均成立。

4.2新方法的实验结果分析

在解决均匀功率谱信号相位编码公式中修正项的取值问题时，为提高遗传算法的收敛精度，加快收敛速度，采用自适应交叉策略对交叉概率进行自适应调整。在进化的初始阶段，设置较大的交叉概率进行粗略搜索，以保持种群的多样性，而在进化的后期，为防止破坏最优解，选择较小的交叉概率进行细致搜索。主要参数设置为：初始种群数目为50，初始种群范围为（0，1），自变量上下限为（0，1），变异概率固定为0.1，初始交叉概率设为0.8。

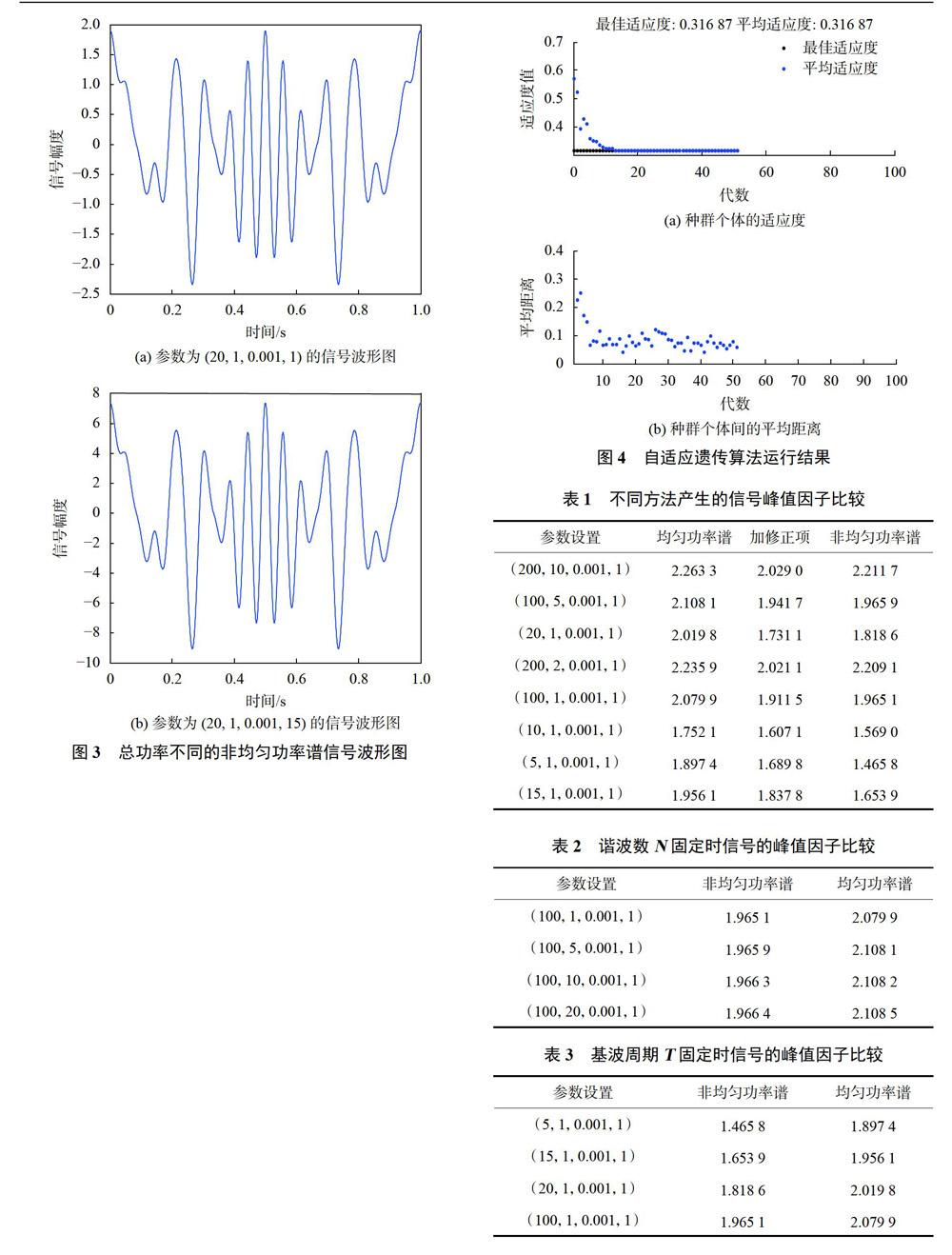
以参数设置为（20，l，0.001，1）的均匀功率谱信号为例，应用自适应遗传算法运行结果如图4所示，解算结果为：修正项ε=0.127，峰值因子CF=1.7311。

设置不同的信号参数，将相应的均匀功率谱信号、加修正的均匀功率谱信号和非均匀功率谱信号的峰值因子进行对比，结果如表1所示。

由表可知，添加修正项的均匀功率谱信号和应用二次正弦调制的非均匀功率谱信号均能有效降低信号的峰值因子。添加修正项的均匀功率谱信号更适合大频带测试，而应用二次正弦调制的非均匀功率谱信号更适合小频带测试。

实验还发现，对于均匀功率谱信号和非均匀功率谱信号来说，信号的峰值因子CF主要与其所含的谐波数Ⅳ有关，基波周期T的影响很小。当谐波数N固定时，基波周期T增大，峰值因子CF增大;当基波周期T固定时，谐波数N增大，峰值因子CF增大，具体实验结果如表2和表3所示。

5结束语

本文研究了多频正弦信号中多谐差相信号的峰值因子最小化问题，该研究方法同样适用于其他多频正弦信号的峰值因子最小化问题。对均匀功率谱信号提出了一种基于自适应遗传算法的相位修正方法，对非均匀功率谱信号给出了二次正弦调制的功率调制通式。通过与标准的均匀功率谱信号进行对比，结果表明本文提出的两种方法均能有效降低信号的峰值因子，添加修正项的均匀功率谱信号更适合大频带测试，而应用二次正弦调制的非均匀功率谱信号更适合小频带测试。