高分辨率光学遥感几何与纹理约束的线段优化算法

2019-06-10戴激光谢诗哲苗志鹏宋伟东朱婷婷

测绘学报 2019年5期

戴激光，谢诗哲，苗志鹏，宋伟东，王杨，朱婷婷

1. 辽宁工程技术大学测绘与地理科学学院，辽宁阜新 123000； 2. 资源与环境信息系统国家重点实验室, 北京 100101； 3. 城市空间信息工程北京市重点实验室，北京 100038； 4. 东华理工大学江西省数字国土重点实验室，江西南昌 330013

作为一种重要的几何基元，线段的方向、长度、端点及线段间的拓扑关系在三维重建、道路提取、建筑物提取、地物变化监测等领域具有较强的应用价值[1-4]。因而近年来国内外学者针对线段检测算法开展了大量的研究。按照文献[5]对线段提取算法的分类，可以分为两类：①全局统计算法，建立符合线性关系的聚类模型，通过解析方式得到参数信息[6-9]；②局部跟踪算法，设定起始跟踪点，根据一定的几何相位约束原则，利用区域增长的方式提取边缘点集，采用拟合方式获取线段参数信息[10-13]。相对于①类算法，局部跟踪算法由于计算量小，因而受到了更广泛的关注[14-16]。在背景相对简单、差异比较明显的近景及航空影像中，目前大多数线段提取算法均有较好的检测效果。然而，在较为复杂实际场景的光学高分辨率卫星遥感影像(空间分辨率优于1 m，以下简称遥感影像)中，一些目视清晰的线状信息依然难以保证线段提取结果的完整性，在道路、建筑物、梯田等具有线性特征的地物中表现尤为突出。这使得线段提取结果长度、端点信息准确性下降，同时也增大了线段间拓扑关系分析的难度，使得线段在遥感影像处理中的应用受到限制。

深入分析现有算法提取线段断裂的因素，可以发现：①地物遮挡，例如树木等对建筑物边缘的遮挡，将导致建筑物边缘的丢失；②边缘影像模糊，实际场景中反差较小的地物间边缘相对模糊，边缘点连续性不强；③边缘锯齿化，噪声、细微地物变化[17]以及推扫式传感器成像过程均易引发边缘锯齿化，使得边缘点间的线性关系不够稳定。由此表明，导致线段断裂的原因一方面是边缘点间连续性不强，另一方面是部分边缘点间难以符合精准化线性要求。而已有线段提取算法均是基于边缘点的连续性和线性准则而提出的，因此线段断裂问题难以避免。而人眼之所以能够观测到完整线状信息，是由于人类能够在视觉环境中组织排列事物的位置，感受和识别出线性地物的连续信息[18]。受到上述思想的启发，一些学者以检测线段为处理基元，利用线段间的几何相位相似性，采用聚类算法[19-20]、跟踪算法[21-23]对提取线段结果进行优化，即将同一地物的断裂线段连接起来，形成完整线段。但聚类算法运行效率较低，并且仅考虑断裂线段间的几何关系，因而精度难以保证。而跟踪算法对线段作为影像特征间的纹理相似特性考虑不足，并且在优化过程中严重依赖于初始优化线段的精度，因而效果难以令人满意。

线段是边缘点的线性聚集体，同时更是地物轮廓表达的一种方式[24]。因此要将断裂线段连接起来，不应仅考虑断裂线段间的几何关系，更应分析断裂线段是否符合同一地物轮廓的纹理相似性。从此思想出发，本文在跟踪算法的基础上，通过对遥感影像线段断裂规律的分析，提出一种基于几何与纹理约束的线段优化算法，并据此给出了完整的算法流程。

1 线段断裂规律

将线段提取结果放入真实场景，有利于对线段断裂规律进行深入分析。图1(a)所示为Worldview-2真实影像，空间分辨率为0.5 m。图1(b)中人工目视道路边缘可视为一条黑色线段，但仔细观察后可以发现道路边缘存在白色遮挡物。因此，利用经典LSD算法[15]进行线段提取后，如图1(c)所示在道路边缘处出现黑色断裂线段。将断裂线段连接起来，优化为图1(b)所示一条线段，需要构建如图1(c)白色连接线段，即将断裂线段连接起来的假设线段，同时也要考虑在同一地物轮廓框架下断裂线段和连接线段的特征。因而本文总结如下：

1.1 几何特征

几何特征主要存在于断裂线段间，这是由于断裂线段是由规则边缘构成，而连接线段为假设线段，不能确保其精确位于地物边缘处，因而几何特征仅适用于断裂线段：

(1) 端点邻近性。图1(c)中所有黑色断裂线段端点和图1(b)所示黑色优化线段间垂直距离应低于一定阈值。

(2) 空间接近性。如图1(c)所示断裂线段端点间空间距离较小，即相邻断裂线段间端点距离符合一定阈值。

(3) 分布有序性。断裂线段集在空间中呈现出同一方向排列有序性，该属性可作为断裂线段跟踪方向的判断依据。

1.2 纹理特征

如果断裂线段、连接线段隶属于一条线段，那么断裂线段与连接线段应相邻于同一目标地物，而同一地物应存在较为一致的纹理相似性，因此需要对线段邻域进行纹理特征分析：

(1) 相位一致性。断裂线段集左右侧灰度对比状况一致。如图1(c)所示，作为线条边缘，所有断裂线段左侧影像相对右侧灰度总体偏低。

(2) 共区域性。如图1(c)所示，断裂线段、连接线段均相邻于道路区域，所有线段左侧均为同一地物，即同侧区域具有纹理相似性。如图1(b)所示，虽然道路边缘属于线条边缘，存在白色遮挡物体，但由于覆盖区域较小，故可通过整体评价其是否符合共区域性要求，因此共区域性以此可作为连接线段、断裂线段的纹理约束条件之一。

(3) 封闭性。封闭性专门适用于连接线段，这一特征可以反向印证连接线段是否为地物轮廓。根据这一特征，如图1(c)中白色连接线段理论应为不同地物间分割线，故连接线段两侧纹理应具有一定的差异性，以满足地物边缘特性。如图1(b)所示，连接线段左侧虽然受到白色遮挡地物影响，但由于其仅占据较小断裂区域，故图1(c)中白色线段两侧可以构成一定的纹理差异性，可满足封闭性特征。

图1 线段断裂示意Fig.1 Schematic of line segment fracture

2 算法原理

根据感知编组非偶然性定律，影像特征呈现某种有序结构绝非偶然[25]。因而当多条断裂线段符合上述特征规律时，可以建立线段优化模型。线段提取结果是优化算法的基础，本文选取一种链码跟踪与相位结合的线段提取算法[5]。该算法优点在于能够确保构成线段的边缘点相位一致性，同时最大程度提高线段检测结果的长度。在线段提取过程中，本文将记录每条线段的多个参数信息(thera,xstart,ystart,xend,yend,flength,Np)。其中，xstart、ystart、xend、yend分别为线段两端点x向与y向坐标；flength为线段长度；Np为拟合当前线段的所有边缘点；thera为线段相位，该参数近似垂直于线段角度，主要反映线段两侧的灰度对比情况，计算公式如下

(1)

式中，Np为构成线段的边缘点数量；ang(i)为第i个点边缘点梯度方向，其范围为[-π,π]。

2.1 线段优化模型

按照数字图像理论，噪声通常是随机存在的，其符合线性规则特征的概率必然较小。反之若线段长度越大，其符合实际地物边缘的概率越高，但同时受到噪声干扰的可能性也相应增大。因此本文首先利用文献[5]算法提取线段，根据线段长度优先的原则确定初始优化线段，其次建立几何约束模型，再次建立纹理约束模型，最后动态更新优化线段及跟踪区域，以此完成对线段优化模型的构建。

2.1.1 几何约束模型

在实际场景中，线段提取结果数量上呈现出海量化的特点，同时相互间存在错综复杂的空间拓扑关系，例如建筑物和道路、道路两侧边缘、农田与道路等线状地物间存在角度相似、距离相近的特点。

因此在进行断裂线段搜索过程中，首先需要确定跟踪范围。

(1)跟踪矩形。依据分布有序性，断裂线段应位于待优化线段延长线方向上，因此如图2(a)所示，可依据端点坐标A(xstart,ystart)和B(xend,yend)向两侧外延确定跟踪方向。根据端点临近性、空间接近性，断裂线段一侧端点必然位于待优化线段端点临近区域内。因此如图2(b)所示，本文以端点A为起始跟踪点为例(B点类似)，建立一个长度为Ls(像素)，右侧距离为Lwr(距离为正值，单位为像素)，左侧距离为Lwl(距离为负值，单位为像素)的灰色矩形。在此跟踪矩形内，线段L1按照跟踪方向遍历断裂线段端点。

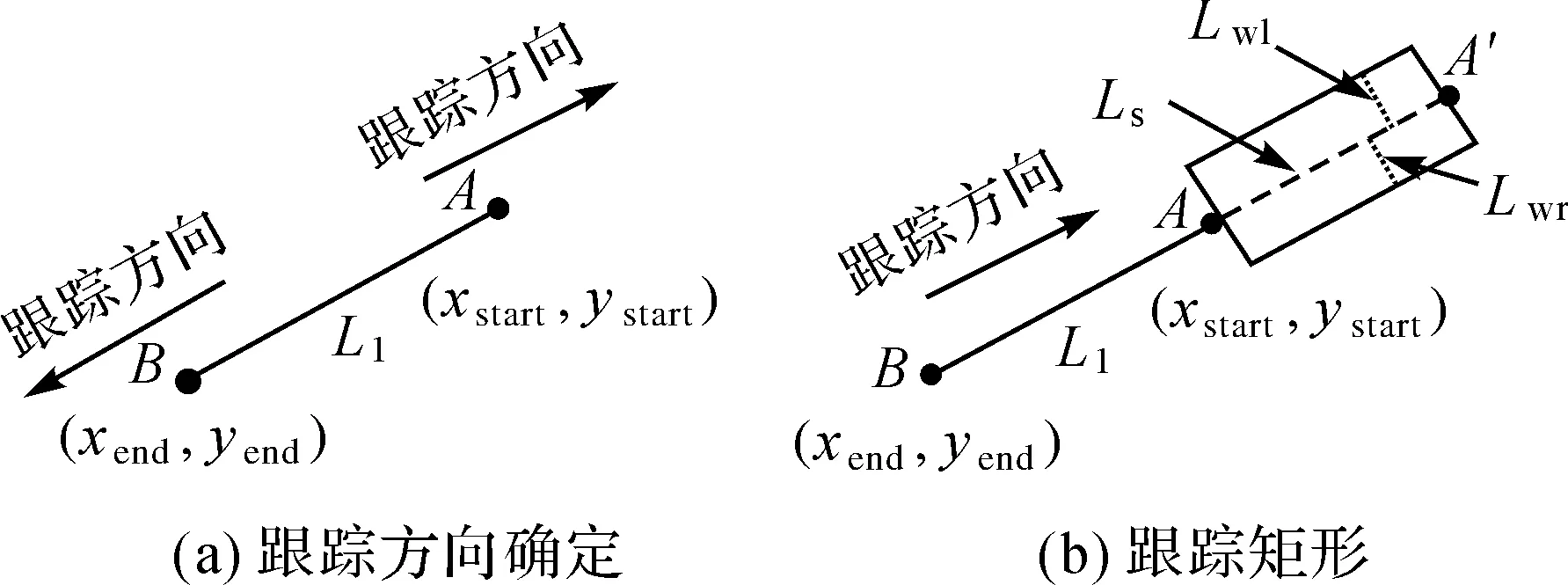
图2 跟踪矩形Fig.2 Tracking rectangle

(2) 位置约束。对大量实际场景线段断裂问题的分析表明，当一条线段两端点位于待优化线段跟踪方向两侧时，人眼一般将其视为相同线状地物，可视其为断裂线段。反之当两端点位于待优化线段同侧且与其存在一定距离时，人眼很难将其视为待优化线段的断裂线。在此思想的启发下，本文首先确保线段两端点坐标(i,j)和(i′,j′)与待优化线段之间的距离D(i,j)和D(i′,j′)均位于[Lwr,Llr]范围之内；其次保证D(i,j)和D(i′,j′)累积绝对值和低于阈值ε。上述两条件构成断裂线段的位置约束条件。具体公式如下

a×x+b×y+c=0

(2)

D(i,j)=(a×j+b×i+c)/sqrt(a×a+b×b)

(3)

abs(D(i,j)+D(i′,j′))<=ε

(4)

式(2)中，(x,y)为待优化线段任意点坐标；a、b、c为线段参数；式(3)中，以待确定线段任意端点(i,j)为例，计算其端点(i,j)与待优化线段间的距离D(i,j)；式(4)中，ε为D(i,j)和D(i′,j′)端点累加距离阈值。

(3) 拓扑约束。图3(a)、(b)中，与白色矩形框连接线段为待跟踪线段。按照位置约束，图3矩形框内白色线段和图3(b)黑色线段作为待确定断裂线段均符合式(4)要求，但明显可以看出图3(a)矩形框内白色线段为正确线，而图3(b)黑色线段为错误断裂线。因此在位置约束的基础上，需进行拓扑关系约束。如图3(b)所示，由于一侧端点已位于矩形跟踪区域内，因此仅需对另一侧端点进行分析，确保该端点位于下侧跟踪线方向上。

dis_pro_S+dis_pro_E>dis

(5)

式中，dis_pro_S为待确定线段端点在待跟踪线段上投影点与待跟踪线起始端点间的空间距离，dis_pro_E为投影点与待跟踪线结束端点间的空间距离，dis为待跟踪线段长度。当线段端点满足式(5)时，则说明其符合拓扑约束。

图3 拓扑约束Fig.3 Topology constraint

2.1.2 纹理约束模型

纹理约束模型是将线段置入实际影像中进行分析，以确定断裂线段是否满足同一地物轮廓要求。因此，本文将依次开展相位约束、共区域性约束及封闭性分析。

(1) 相位约束。依据相位一致性原则，将相位约束设置为待确定断裂线段的纹理约束条件之一。相位约束公式如下

abs(theraref-therasrc)<=η

(6)

式中，theraref为待优化线段相位；therasrc为待确定断裂线段相位；η为相位阈值。

(2) 共区域性约束。根据共区域性特征，断裂线段、连接线段均应相邻于同一地物。因此本文针对共区域性特征，提出一种整体匹配评价算法。如图4所示，首先在黑色实线(断裂线段)、黑色虚线(连接线段)左右根据距离线段为2像素(设置短距离是为了适应线条边缘的特点)，步长为5像素抽取黑色点为抽样点；其次在整体匹配评价中，对灰度值进行重新量化(以8 bit影像为例，可将其线性压缩为4 bit)，以解决线段边缘附近纹理均质化较差的问题；最后，针对线段边缘影像易发生灰度跳变的问题，建立种子点为圆心半径为1的圆形模板。确定模板值的公式如下

(7)

式中，M为圆形模板；Im为圆形模板的灰度均值；Igm为圆形模板的灰度直方图峰值。

依据图4与式(7)可给出具体步骤：首先，利用式(7)在断裂线段、连接线段两侧分别计算其抽样点模板值M；其次，利用线段相应方向进行匹配，即2条断裂线段与连接线段左侧模板均值进行比较，如差值均低于2，则说明满足左侧共区域性特征，反之进入右侧共区域性约束判断。

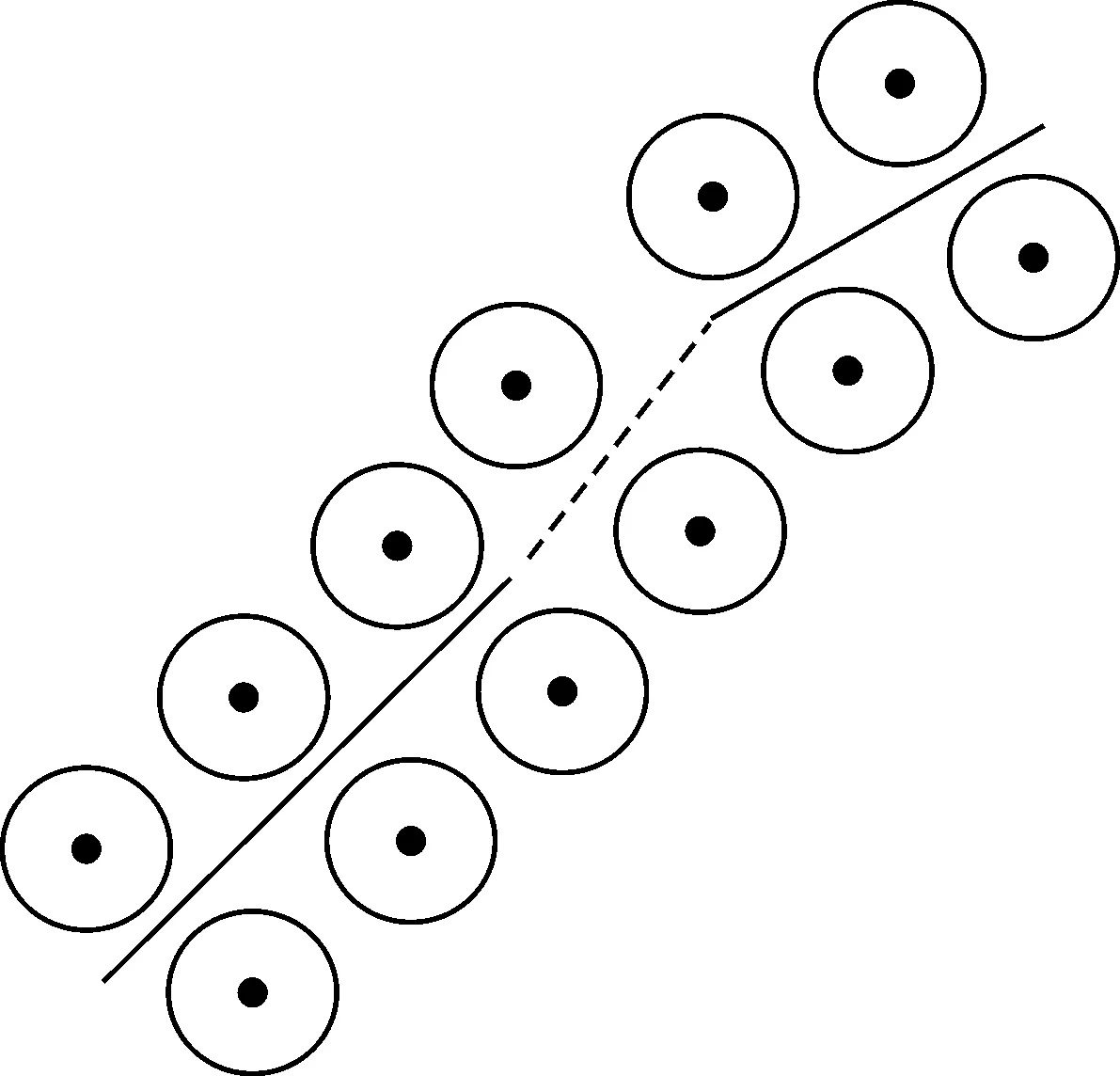
图4 共区域性约束Fig.4 Common regional constraints

(3) 封闭性分析。封闭性分析主要是针对线段优化过程中的过提取问题。如图5所示为两条黑色线段为真实提取线段，依据线段几何约束模型两条线段完全满足要求，同时2条线段右侧为同一地物也符合相位约束和共区域性，但两条线段明显不是断裂线段。如何避免将2条线段连接起来，需要对连接线段所在区域进行封闭性分析。在分析过程中，可参考图4在连接线左右抽样统计模板值。如两侧值差异绝对值低于2，说明当前为错误连接线段，反之高于2则说明连接线符合封闭性要求，可进行线段优化。

图5 线段过提取问题Fig.5 Problem of line segment over extraction

2.1.3 线段动态优化模型

受到边缘锯齿化的影响，初始优化线段与实际地物边缘并不能完全吻合。因此需要动态优化线段，以确定新的跟踪端点及跟踪范围，避免当初始优化线段出现位置偏差时，导致最终提取的优化线段精度受到影响。本文利用每条线段提供的边缘点集，采用最小二乘法计算线段参数，并利用边缘点在该直线上的投影范围确定优化线段端点，同时更新优化线段参数信息(thera,xstart,ystart,xend,yend,flength,Np)。

2.2 算法步骤

依据上述线段优化提取模型，图6给出了本文算法的技术流程。

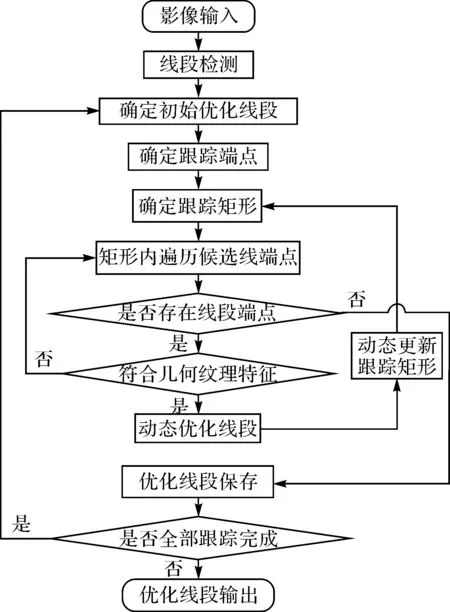
图6 技术流程Fig.6 Technical flow chart

(1) 线段数据集与端点矩阵构建。以线段提取结果作为处理基元，按照线段长度由大到小的顺序将其存入数据集N中。该数据集依次记录每条线段属性及该线段在数据集中的序号。以线段端点空间位置为基础，构建端点矩阵M1。M1的大小与影像大小一致

(8)

式中，mij记录对应影像位置(i,j)上是否存在线段端点，有则直接记录线段在N中的序号，没有则为0；k和n分别为影像行列数值。

(2) 初始优化线段确定。在数据集N中按照存储顺序依次抽取线段，如果该线段端点在矩阵M1非0值，则将其设为初始优化线段，基于初始优化线段端点建立跟踪矩形，双向跟踪并进入步骤(3)；如为0值，则再次进入步骤(2)。

(3) 在跟踪区域内遍历线段端点。依据搜索区域及跟踪方向，遍历线段端点信息，如存在则进入步骤(4)，否则进入步骤(6)。

(4) 几何和纹理约束分析。依据几何约束模型和纹理约束模型，对待确定断裂线段进行分析，判断其是否要求，满足则进入步骤(5)；不符合条件则进入步骤(3)。

(5) 优化线段端点与跟踪区域更新。基于线段所提供的边缘点集，动态优化线段及其参数，并由此确定新的跟踪端点及跟踪矩形，进入步骤(3)。

(6) 优化线段分析。存储新优化线段，并判断优化线段是否已经全部处理，如未处理则进入步骤(2)，反之若全部处理完毕则输出所有优化线段。

3 试验

3.1 参数分析及设定

为解决遮挡、边缘模糊和锯齿化等问题对线段优化的影响，本文算法需要设定多个参数阈值。由于本文所选取的遥感影像空间分辨率均在0.5～0.8 m，分辨率相差不大，因此依照阈值最大适应性原则，对各个参数设定经验阈值，并对定量设定结果及其原因进行讨论：

(1) 跟踪矩形参数。跟踪矩形的设定主要是为了克服遮挡、边缘模糊化和锯齿化对线段断裂的影响。本文设定Ls为20像素；左侧距离Lwl为-8像素；右侧距离Lwr为8像素。

(2) 几何约束阈值ε。当线段与待优化线段近似平行且有较大的距离，人眼倾向于将其视为不同线段，几何阈值参数ε就是针对这一问题建立的定量化几何约束条件。经过多次试验验证，本文将这一阈值设定为8像素。

(3) 相位约束阈值η。该参数是为了消除边缘锯齿化对线段断裂的影响，本文设定η为π/9弧度。

3.2 试验结果与分析

在试验中，本文算法以VS2010为运行环境，利用C++编程进行试验分析。在选取对比算法时，分别选取具有代表性的线段优化算法，即文献[21，22]算法进行对比分析。文献[21]算法从几何拓扑关系和物理光谱信息两个方面对线段进行优化，并利用C++编程方式实现；文献[22]算法则利用线段图模型对线段间的连接关系进行估计、验证，以此进行线段优化，该试验结果由笔者提供的Matlab代码处理得到。相对而言，文献[21]算法是几何拓扑与光谱信息的结合，而文献[22]算法更加侧重于几何关系的分析。在试验中，本文首先选取一幅城郊高分辨率遥感影像，分别展示加入几何约束和纹理约束后线段优化结果，以验证将几何与纹理约束进行线段优化的必要性；其次，分别选取了具有代表性的2幅不同类型的遥感影像进行算法分析，覆盖区域分别对应于城市、农村，其中包含遮挡、模糊化、边缘锯齿化所导致的线段断裂问题。在线段优化结果精度检验过程中，由于优化线段数量不大，因此本文采用目视检验的算法进行精度分析。

3.2.1 试验1

图7(a)所示为辽宁省葫芦岛市某地区的GF-2卫星影像，空间分辨率为0.8 m，影像大小为1500×1500像素，覆盖范围为城郊区域。直接对影像进行线段提取，可获得7875条线段。经过优化后变为7504条线段，其中优化线段为150条，错误线段为3条，耗时为67.5 s。由于线段检测结果数量较大，为了清晰展示线段提取及优化结果，如图7(a)所示对局部影像进行放大，可以发现该区域为小区门口，存在较多线状信息。同时也可以看到，受到边缘模糊化的影像，道路边缘线段明显出现了断裂。采用如图7(b)所示的几何约束优化，可以看到道路线已经被连接起来，但出现了过连接问题，最突出的就是小区门口已经被道路线连接，并且小区内的线段也存在过连接问题。如图7(c)所示，本文在几何约束的基础上引入纹理约束，可以看到由于过连接线段不满足封闭性，故两条白色线段的过连接问题已被处理，由此说明本文纹理约束的必要性，也验证了几何与纹理相结合优化线段算法的可靠性。

3.2.2 试验2

图8所示为辽宁省葫芦岛市某农村的Pleiades光学高分辨卫星遥感影像，空间分辨率为0.5 m，影像大小为632×679像素，覆盖区域内包含平房、道路等线状信息，利用线段提取算法可检测到1675条线段。如图8(a)线段提取结果放大图显示，道路受到两侧树木阴影遮挡的影响，存在断裂现象。如图8(b)所示为本文算法线段优化结果。对放大图白色优化线段分析后可以发现，由阴影遮挡所导致的线段断裂问题也已解决。同时对比文献[21]算法中的优化结果，可以看到建筑物白色线存在过连接问题，同时由于遮挡所导致的线段断裂问题也未解决。对比如图8(d)结果可以明显发现，文献[22]算法优化线段与边缘吻合度非常高，但遮挡导致的线段断裂问题基本没有解决。

3.2.3 试验3

图9所示为澳大利亚某地区的GeoEye-1影像，空间分辨率为0.5 m，影像大小为1024×1024像素，覆盖区域为城区。在图9(a)线段提取结果局部放大图中，受到边缘锯齿化影响，道路边缘提取线段结果存在交叉的现象。如图9(b)所示，利用本文算法能够基本解决锯齿化问题，并且线段优化结果基本符合人工视觉。而图9(c)利用文献[21]算法，优化后的部分线段存在较大的位置偏差，这说明该算法对于线段间纹理约束的分析不足，因而降低了优化线段结果的精度。同样对比图9(d)，可以看到文献[22]算法对于边缘锯齿化问题处理能力不足，因而道路线断裂问题依然存在。

图7 线段优化过程Fig.7 Process diagram of line segment optimization

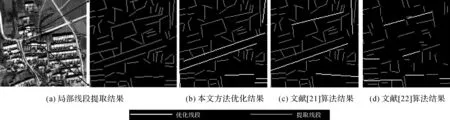
图8 Pleiades影像线段优化效果Fig.8 Line segment optimization results for Pleiades image

图9 GeoEye-1影像线段优化效果Fig.9 Line segment optimization results for Pleiades image

基于城市、农村及城郊不同实际场景，采用不同类型的高分辨率遥感影像数据，通过对比可以明显看到本文算法具有解决线段断裂问题的能力。由于优化后不同算法线段数量并不一致，全部分析线段并不反映本文算法解决遮挡、模糊化、锯齿化问题的能力，因此本文仅选取符合一定条件的线段进行优化。这是由于实际遍历初始优化线段和最终形成优化线段的数量比例通常为5∶1，大量线段不需要进行优化处理。例如图8需要优化90条线段，但实际初始优化线段需要461条。因此从提供算法效率的方面考虑，本文根据不同的影像选择不同数量的优化线段。如表1所示，通过对比本文与文献[21]算法优化线段提取精度，可以看到本文算法优化精度(95.7%)明显高于文献[21]算法(82.1%)，低于文献[22]算法。但文献[22]算法对于锯齿化、模糊化、遮挡问题解决能力不足，虽然精度很高但优化线段平均长度很低，无法将断裂线段连接起来，难以满足实际场景遥感影像处理需求，这从优化后线段总长度和平均长度可以清楚看出。同时对比不同算法的运行耗时，可以看到本文算法低于文献[21]算法。这是由于本文算法加入更多的纹理约束条件，降低了算法的速度，另外也说明本文算法需要进一步提高效率。

表1 不同算法线段优化结果

Tab.1 Line segment optimization results by different algorithms

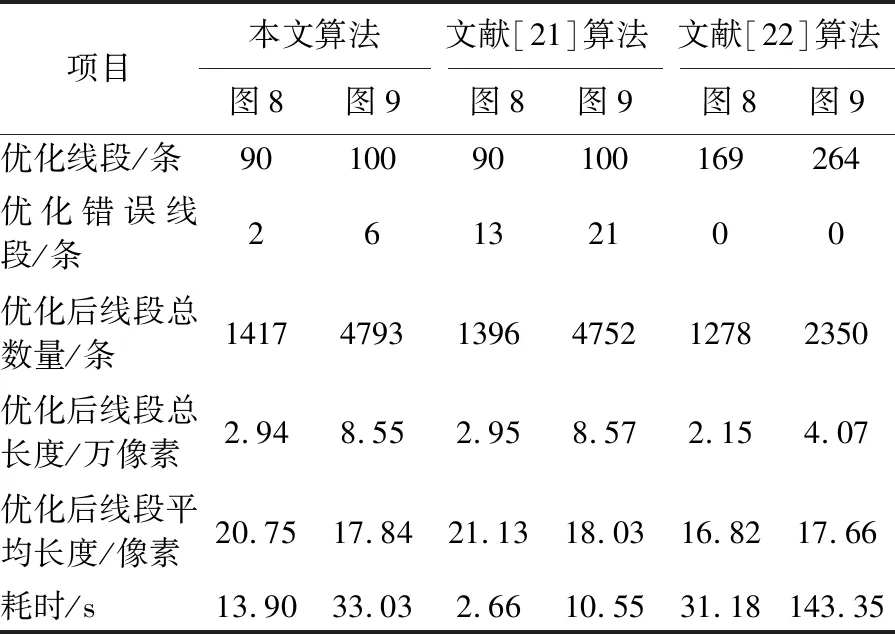
项目本文算法文献[21]算法文献[22]算法图8图9图8图9图8图9优化线段/条9010090100169264优化错误线段/条26132100优化后线段总数量/条141747931396475212782350优化后线段总长度/万像素2.948.552.958.572.154.07优化后线段平均长度/像素20.7517.8421.1318.0316.8217.66耗时/s13.9033.032.6610.5531.18143.35