多窄路口下改进的bi-RRT路径规划
2019-06-10龙建全张皓然梁艳阳
龙建全,张皓然,梁艳阳
(西南科技大学信息工程学院,四川绵阳 621010)
0 引言
在机器人运行的研究中,路径规划成为了研究的重点之一。路径规划即从初始位置找到一条通向目标位置的无碰撞路径,同时兼顾环境约束和移动体自身存在的约束[1]。传统的路径规划算法有A*、人工势场、蚁群算法等。而这些算法存在自身的问题,例如A*算法要求的计算量较大[2],人工势场法容易使机器人陷入局部最小值中[3],蚁群算法收敛速度慢[4]。这些算法不能适应多障碍物条件下的求解,不能适用于机器人的运行。许多学者在机器人领域,尤其在面向复杂环境下的路径规划成为当今研究的重点范围。S. M. LaValle等于1999年提出了基于随机采样的快速扩展随机树(Rapidly exploring Random Trees,RRT)[5],相比于传统的路径规划算法,它的优势能在复杂环境下找到一个收敛的解,不需要对工作空间做一些预处理,而传统方法有些需要对环境做预处理,部分传统算法不一定能找到收敛解。搜索速度相比传统算法要快。但RRT算法也存在一些问题,例如均匀采样搜索的范围大搜索时间较长,得到收敛解的时间长。在一些狭窄路口不能找到解,容易陷入局部最小。传统的RRT算法并没有结合车辆的非完整约束,使得求出的路径不可行。针对不同模型的车辆度量函数的选择也会制约算法的搜索效率。算法生成的路径不平滑,拐点众多等问题。
针对上述问题,国内外有学者提出相应的优化算法,W. Wang等提出了“桥测试”方法[6],该方法主要通过在起点、终点和桥测试点同时生成树,通过多树的不断结合生成路径,但是在复杂环境下得到收敛解的时间过长。刘多能提出的方法是通过人为的主观判断,在狭窄路口设置虚拟点来引导扩展,虽然在狭窄路口数量少时,人为可以判断,但是狭窄路口过多就不利于人为判断,会造成算法收敛时间过长[7]。I.A.Sucan等人提出了在动力学模型的基础上进行动态规划[8]。尹高扬提出了根据无人机动力学模型下的RRT扩展,应用于非完整积分约束下的路径规划[9]。刘华伟提出了陷阱环境下设置虚拟目标点的引导来解决局部最小的情况[10]。杜明博提出一种基于连续曲率的路径规划,让汽车运动的曲率保持连续[11]。一些学者也结合一些拟合函数例如B样条[11]、贝塞尔曲线[12]和树枝修剪的后期处理技术来解决路径不平滑的问题[13-14]。
本文针对多路口的复杂环境下小车的路径规划,提出一种人工设置多虚拟目标引导区域的bi-RRT路径规划算法[15](bi-RRT with mutiply artifical guided region,bi-RRT-MAGR)。首先根据路口设置路标点,在根据其连通域通过Dijkstra找出以这些点连接的最短路径构建采样区域集合,满足小车非完整约束的处理,来解决RRT存在不足的问题。最后通过仿真实验来验证其合理性、高效性和正确性。
1 非完整约束模型
非完整约束系统通常受到空间位置以及其运动速度的影响,使速度的积分不能转换为系统空间的位置。由于其不可积的约束存在,使得其运动的控制与规划变得复杂。对于一般的非完整约束系统:
(1)

(2)
则判定该系统为完整约束系统,否则为非完整约束系统[16-17]。

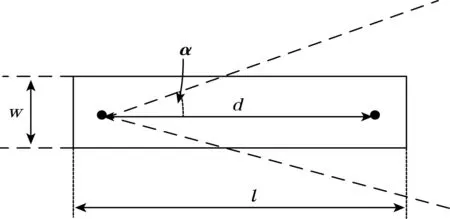
图1 非完整约束小车模型
图1为典型的非完整约束小车模型,(x,y)为当前小车在全局坐标系下的位置,θ为小车主轴方向与全局坐标下x轴方向的夹角,L为小车车长(即前轮与后轮之间的长度),ρ为小车的转弯半径,v为小车的速度,φ为小车与小车主轴方向的夹角(转弯角)。小车的车轮只能做纯滚动、无滑动的运动,无论任何时候小车的方向一定指向小车的主轴。在Δt近于零时,小车车体所受的约束为

(3)
也可以表示为

(4)
由图可知,vi为车体速度的积分。

(5)
(6)
小车的状态转移方程如下:
(7)
(8)
小车的转向角和速度必须满足不能超过其最大转向角和最大速度的约束条件(如式(8))。
通过结合非完整约束小车的模型,给定xt的位置、方向角以及转向角,小车速度v,小车车长L和时间差 Δt=dt,得到xx+Δt的相应的位置和方向角,生成方式如式(9)(函数generate):
(9)
2 多引导域的bi-RRT算法
本文提出一种混合策略的bi-RRT,首先通过人为在狭窄路口的入出口设置虚拟目标点,并用Dijkstra算法[18]根据这些虚拟目标点找出他们最短路径的集合并用作bi-RRT树扩展中的采样区域。该算法能使bi-RRT迅速通过狭窄路口和大幅减少算法的搜索时间,以提高算法的效率。
2.1 基本的RRT算法
X⊆Rd,X为工作空间,Xobs⊂X为障碍物区域,Xfree=X/Xobs为自由区域,Xinit为起始点位置,Xgoal为目标点位置。Xnew为新生成节点,Xclosest为最临近点。路径规划问题本质在于找到一条collisionfree pathσ,v表示小车速度,连接阈值为threshold,连接角度阈值为thresholda ngle,V为节点集合,E为边的集合,Tree为扩展树。
Sample:采样函数从Xfree返回一个独立的值Xrand作为采样点。
Nearest:给定一个点Xclosest∈V,使得T(Xclosest,Xrand)值最小。
Steer:扩展函数返回一个值Xnew,根据式(9)。
CollisionCheck :检测两节点间是否有障碍物碰撞。给定2个点Vertex1,Vertex2,根据公式Vertex=λ·Vertex1+(1-λ)·Vertex2,λ∈[0,1]来判断Vertex是否与障碍物碰撞。
PathToGoal:存在节点Xnew∈V,使得‖Xnew-Xgoal‖ Steer:函数通过最临近点Xclosest,通过φ的增量变化,生成多条路径path,再根据欧式距离找出离随机点Xrand最近的一个点作为新节点Xnew。 RRT伪代码如下: V←{Xinit,Xgoal};E←φ;Tree←(V,E); fori=1 toNdo Xrand←Sample; Xclosest←Nearest(Xrand,Tree); Xnew←Steer(Xclosest,Xrand); if no CollisionCheck(Xclosest,Xnew) Tree←Xnew∪Tree; if PathToGoal(Xnew,Xgoal) Tree←Xgoal∪Tree; 传统的RRT是一种单查询方式的搜索树,通过给定的Xinit和Xgoal,在工作空间生成随机点Xrand,根据欧氏距离找到树上的最临近点Xclosest,在以给定的参数生成新节点Xnew,通过不断的迭代,直到新生成的Xnew与Xgoal的欧氏距离小于阈值时,通过Xgoal寻找其父节点回溯到Xinit,就可以得到一条完整路径。 首先是通过人为主观的在狭窄路口设置虚拟目标点如图2,0和9分别为起始点与目标点,1~8是人为设置的虚拟目标点。 图2 人为设置的虚拟导航点示意图 定义1 加入起始点和终点来构建点之间的权值矩阵W,dij作为两个连通域间的欧氏距离,用∞表示两个非连通域,规定入口与入口不为连通域,入口与出口互为连通域(入口与出口间不能有其他入出口)。 定义2 在多路口环境下通过人为设置路标点(Landmark),通过Dijkstra找出节点间的最短路标索引,可定义为向量Landmark={Lm1,Lm2,…,Lmn},n为索引出来的路标点个数: Dijkstra算法步骤 (1)集合S={0},0为起始点,V={0,1,2,…9},U=V-S。 (2)从U中选取一个距离0结点最近的点k,把k加入到S,并从U中删除。 (3)如果d0u>d0k+dku,则d0u=d0k+dku。 (4)重复步骤(2)、(3)直到所有点都在集合S中。 Dijkstra是一种根据点的连通域来求解的算法,通过输入起始点和相应的权值矩阵[18]。根据算法特性和多次的迭代求出一组最短路径的点集合Landmark。 ForwardRegion(Landmark)函数:根据找出的Landmark,建立连续的采样区间,当扩展树到达第1个节点时,仅在第1个节点与第2个节点间长l宽w的矩形范围采样。当存在节点到达第2个节点时,则采用第2个节点与第3个节点间的矩形范围采样,依次类推(见图3)。生成随机点的角度与当前矩形主轴的角度小于α时,成功生成随机点,如图4所示。 图3 采样区域连接图 图4 重叠采样区域 ReverseRegion(Landmark)函数:根据找出的Landmark,建立连续的采样区间,当扩展树到达倒数第1个节点时,仅在倒数第1个节点与倒数第2个节点间长l宽w的矩形范围采样。当存在节点到达倒数第2个节点时,则采用倒数第2个节点与倒数第3个节点间的矩形范围采样,依次类推。生成随机点的角度与当前矩形主轴的角度小于α时,成功生成随机点。 采样函数Samplefrom Landmark伪代码 if Treea ForwardRegion(Landmark) if abs(Sample-mainangle)<α samplesuccess if Treeb ReverseRegion(Landmark) if abs(SampleAngle-mainangle)<α samplesuccess 根据上述Dijkstra找出的最短路标集合,对于以起始点生长的树Treea,选择路标集合Landmark中的第1个路标和第2个路标构建采样区域。当Treea存在节点到第1个路标点的欧氏距离小于阈值,则把第2个路标点和第3个路标构建采样区域,如果Treea存在节点到第2个路标点的欧氏距离小于阈值,则把第3个路标点和第4个路标构建区域,依次类推下去。对于以目标点生成树Treeb,则以最后1个路标点和倒数第2个路标点构建采样区域,当Treeb存在节点到最后1个节点的欧氏距离小于阈值时,则以倒数第2个路标点和倒数第3个路标点构建区域,依次类推,不断地产生采样空间。而本文提出的路标点构建的采样空间,能引导机器人快速的向狭窄路口靠近并通过它同时大幅减少收敛时间,提高算法的效率。 通过上述对小车模型的分析、引导点的选择、采样空间的确定以及对基本的RRT算法的了解。提出了一种基于多引导点区域的bi-RRT算法。 bi-RRT-MAGR的伪代码: Va←{Xinit};Vb←{Xgoal};Ea,Eb←φ; Treea←(Va,Ea);Treeb←(Vb,Eb); fori=1 to toNdo if Threea Xrand←SamplefromLandmark Xclosest←Nearest(Xrand,Tree); Xnew←Steer(Xclosest,Xrand); if no CollisionCheck(Xclosest,Xnew) Treea←Treea∪Xnew if Treeb Xrand←SamplefromLandmark Xclosest←Nearest(Xrand,Tree); Xnew←Steer(Xclosest,Xrand); if no CollisionCheck(Xclosest,Xnew) Treeb←Treeb∪Xnew if PathToGoal(Treea,Treeb) break Tree←Treeb∪Treea 以起始点init开始构建Treea和目标点Xgoal构建Treeb,设置最大迭代次数N,Treea和Treeb通过SamplefromLandmark函数获取相应的采样区域,以Nearest函数找出相应树的最邻近点,再根据最临近点通过Steer函数不断生成新节点,判断新生成的节点与最临近点之间是否存在碰撞,如果不存在则相应的树加入新节点,直到Treea和Treeb两棵树存在节点满足函数PathToGoal并判断两点是否存在碰撞,若否定则搜索结束。在根据两棵树的连接点分别进行父节点的索引直到回溯到起始点和目标点,将两棵树的点集合合并,最后得到一条完整的路径。 根据上述算法设计,本文在Inter Core i5-7500,主频3.4 GHz PC机上采用MATLAB 2016a上进行算法编程仿真测试。设定小车速度为v=5 m/s,时间差Δt=0.5 s,小车车长L=7.5 m,最大转弯角φmax=0.7rad。地图1的起始点(400,50),目标点(50,500)。地图2的起始点(400,50),目标点(50,950)。图5、图6图中,地图(0,0)位置在左上角,竖直向下为x轴正方向,横向向右为y轴正方向,通过Dijkstra找出的路标索引点见表1。 表1 通过Dijkstra找出的路标索引点 图5 地图1情况下算法生成路径图 图6 地图2情况下生成路径图 在图5和图6,左边为搜索路径,右边为最终路径。由图5对比得,在地图1的情况下,狭窄路口数量不多,RRT在搜索范围几乎充满整个空间,搜索时间相对较长,bi-RRT相对于RRT在搜索效率上和收敛次数上提升了1倍,通过表2得出本文改进的算法,在搜索效率上相对bi-RRT提高了1倍。由图6对比,在地图2的情况下RRT搜索由于不能正确的找到路口,路径会搜索更长,而本文提出的算法就是按照Dijkstra索引出的最短路标点构建的采样区域,在路径搜索上相对于RRT、bi-RRT要短一点,主要原因是RRT,bi-RRT在搜索上具有随机性,他们既能向其他距离比较远的路口搜索,也可以向距离较近的搜索,而本文会向路标索引处大范围搜索,所以平均距离短一点。通过表3在搜索效率上相比于RRT提高了7~8倍,相对bi-RRT提高了3~4倍。根据地图1与地图2的仿真实验,本文所提算法相对其他两种算法在搜索效率和收敛次数更加高效和合理。 表2 地图1情况下算法对比 表3 地图2情况下算法对比图 本文针对非完整约束小车的路径规划和RRT算法所出现的随机性太强,获得路径的时间长,搜索范围广和收敛慢等问题,提出了基于虚拟目标区域导航的bi-RRT算法,该算法继承了bi-RRT的随机性、兼顾小车的非完整约束。通过多路标区域的引导使算法不会在路口等狭窄位置重复搜索,使搜索快速通过路口,最后产生合理的路径,使得规划出来的路径更加满足实际的需要。通过仿真实验验证该算法的有效性,对于提高小车在实际路径规划具有实际意义。2.2 引导点的选择

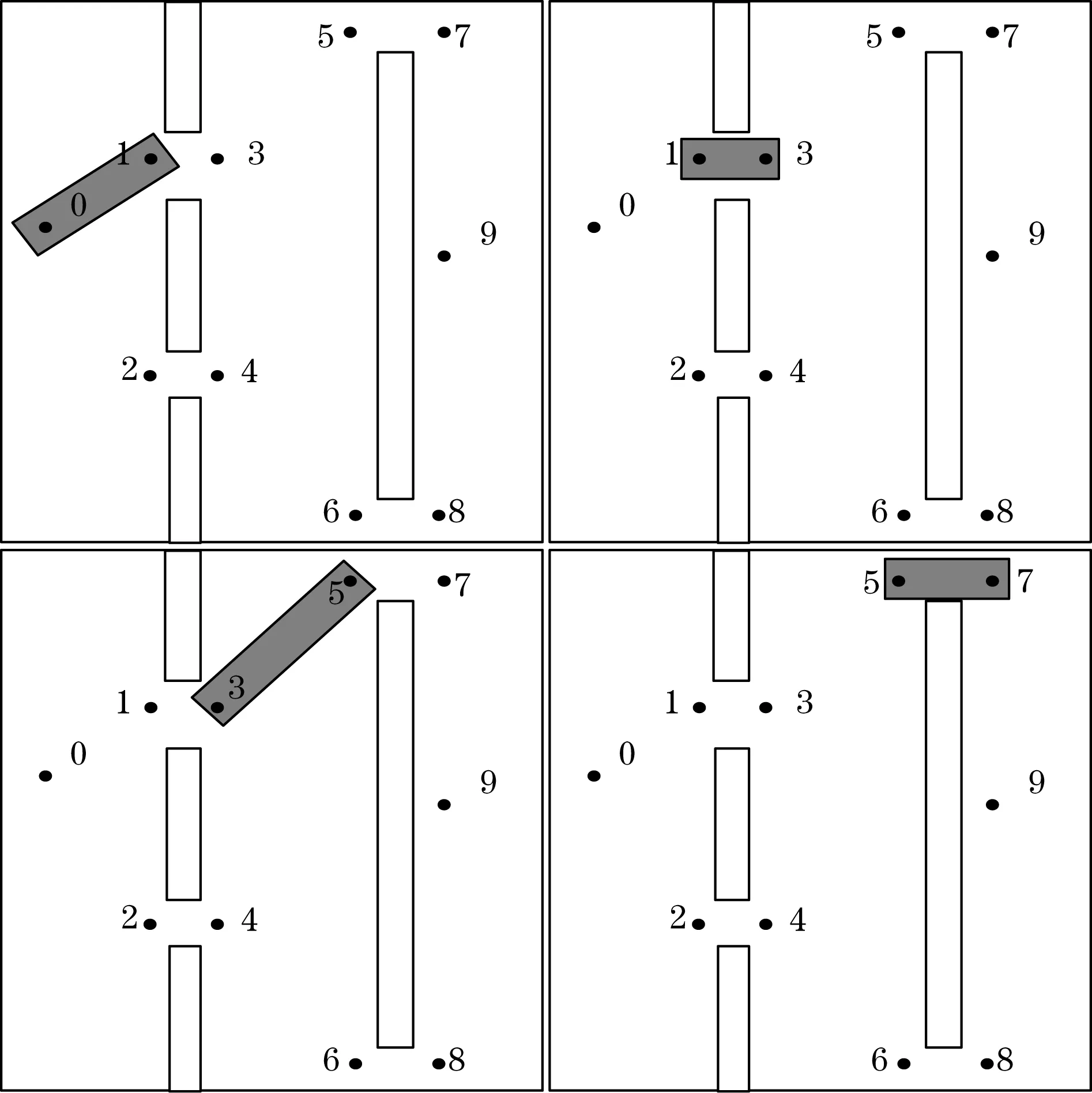
2.3 bi-RRT-MAGR算法
3 仿真实验与分析





4 结论
