正余弦优化算法在多阈值图像分割中的应用

鲍小丽　贾鹤鸣　郎春博　彭晓旭　康立飞　李金夺

摘 要：阈值的选取对图像分割后的效果有重要的影响， 在传统的图像分割中存在分割结果单一，灵活度不强，以及容易陷入局部最优的问题。为了确定图像分割的最佳阈值， 本文针对图像分割过程中涉及的阈值选取问题， 提出一种基于正余弦优化算法（sine cosine algorithm， SCA）的多阈值图像分割方法。该算法以最大类间方差作为正余弦算法的适应度函数，通过正弦函数和余弦函数的变化来更新当前解在每一维度上的位置，候选解利用多个随机算子围绕最优解进行正余弦的波动来完成每一次的寻优过程，通过迭代计算更新最优解的位置， 从而确定图像分割的最佳阈值。选取4幅标准测试图像进行实验，通过与粒子群优化算法进行峰值信噪比、结构相似法和寻优时间3方面的对比，结果表明：将正余弦优化算法应用在图像分割中可以获得更准确的分割阈值和更高的分割效率，具有很强的实用性。

关键词：图像分割;多阈值;最大类间方差算法;正余弦优化算法

中图分类号：TP391.41   文献标识码：A  文章编号：1006-8023（2019）04-0058-07

Application of Sine Cosine Optimization Algorithm to Multi-threshold

Image Segmentation

BAO Xiaoli， JIA Heming*， LANG Chunbo， PENG Xiaoxu， KANG Lifei， LI Jinduo

（College of Mechanical and Electrical Engineering， Northeast Forestry University， Harbin 150040）

Abstract：Threshold selection has an important impact on the effect of image segmentation. In traditional image segmentation， there are some problems such as single segmentation result， weak flexibility and easy to fall into local optimum. In order to determine the optimal thresholds for image segmentation， a multilevel-thresholding image segmentation method based on sine cosine algorithm （SCA） is proposed in this paper. The method takes the between-class variance as the fitness function of the sine-cosine algorithm， updates the position of the current solution in each dimension by changing the sine function and cosine function. The candidate solution uses multiple random operators to carry out sine-cosine fluctuation around the optimal solution to complete each optimization process， and updates the optimum through iterative calculation. The optimal thresholds of image segmentation are determined by the location of the solution. Four standard test images are selected for experiment and compared with PSO algorithm in peak signal to noise ratio， structural similarity method， and optimization time. It shows the application of sine-cosine algorithm in image segmentation can obtain more accurate threshold and higher segmentation efficiency， which has a strong practicability.

Keywords： Image segmentation; multilevel thresholding; Otsu method; sine cosine optimization algorithm

0 引言

图像分割可以将图像细分成多个互不相交的子区域，从而提取出有意义的目标，是图像处理和前期视觉中的基本技术。图像分割的自适应性和正确性在一定程度上影响着目标检测和识别的智能化程度，直接决定了图像分割的质量[1-2]。

阈值法是一种简单有效的图像分割方法，它利用图像中目标与背景在灰度特性上的差异，通过选取合适的灰度阈值对图像进行分割，从而将目标从背景中区分出来。其中利用最大类间方差准则来确定最优阈值是常用阈值分割方法之一[3-5]。該方法在一定程度上可以解决阈值分割中门限的选取问题，但是对于一些灰度直方图的灰度级分布谷底不明显的图像，如果单一的使用最大类间方差法即Otsu算法，就很难达到满意效果，容易陷入局部最优，而且难以适应实时的处理，运行速度较慢，图像分割的质量下降[6];多阈值分割在求解问题时采用的是穷举搜索法，随着分割阈值个数的增加，其计算量呈指数增长，这也直接影响了图像分割的效率[7]。

在正余弦优化算法（Sine Cosine Algorithm， SCA）中会生成多个初始随机候选解，并使它们基于正弦和余弦的数学模型向外波动或向最优解的方向波动，利用多个随机变量和自适应变量来计算当前解所在位置，从而可以搜索空间中的不同区域，有效地避免局部最优，收敛于全局最优。针对上述多阈值图像分割中存在的问题，本文提出一种结合Otsu和正余弦算法的阈值优化选取方法。通过将正弦余弦算法与多阈值图像分割相结合，可以找出灰度区域内最优的阈值组合。与粒子群优化算法（Particle Swarm Optimization， PSO）对比分析[8-9]，记录两个算法的寻优时间，并且利用峰值信噪比和结构相似法对分割后的图像进行评价，通过对数据进行分析比较可知，SCA算法具有原理简单，易于实现，收敛速度快，鲁棒性较好等优点。

1 正余弦优化算法

正余弦优化算法是一种随机优化算法，具有高度的灵活性，原理简单，易于实现，可以方便的应用于不同领域的优化问题。正余弦优化算法的寻优过程可分为两个阶段，在探索阶段，优化算法通过结合某随机解在所有随机解中快速寻找搜索空间中的可行区域;到了开发阶段，随机解会逐渐发生变化，且随机解的变化速度会低于探索阶段的速度。在正弦余弦算法中，首先候选解会被随机初始化，然后会根据正弦或者余弦函数并结合随机因子来更新当前解在每一维度上的值。其具体更新方程为：

Xt+1i=Xti+r1×sin（r2）×r3Pti-Xtir4<0.5Xti+r1×cos（r2）×r3Pti-Xtir4>0.5。（1）

式中：Xti是当前个体的第i维第t代的位置;r2為0到2π的随机数;r3为0到2之间的随机数;r4是0到1的随机数，Pti表示在t次迭代时最优个体位置变量的第i 维的位置。

r1=a-taT。（2）

式中：a是一个常数;t为当前迭代次数;T为最大迭代次数;参数r1表示下一个解的位置区域在当前解和最优解之内或者之外，较小的r1的值有助于增强算法的局部开发能力，较大的r1的值有助于提高算法的全局探索能力，同时r1的值随迭代次数逐渐减小，平衡了算法局部开发和全局搜索的能力;r2，r3和r4为随机因子，参数r2定义了当前解朝向或者远离最优解多远;参数r3为最优解给出一个随机权值，是为了随机强调（r3>1） 或者忽略（r3<1）最优解在定义候选解移动距离时的影响效果;参数r4平等地切换正弦和余弦函数[10]。

对于给出的问题，正余弦优化算法会随机创建一系列候选解，并且根据正弦和余弦函数更新每个候选解在所有维度上的值，正弦和余弦函数的循环模式允许一个解在其他解的周围被重新定位，这能够保证在两个解之间的空间进行搜索。可以更快地收敛于全局最优。

正余弦的寻优过程如图1所示，当正弦或余弦函数返回值在-1和1之间时，候选解可以较好搜索前景的空间，使其得到充分开发;当正弦或余弦函数返回一个大于1或小于-1的值时，候选解可以在探索所定义的搜索空间之外的区域进行全局搜索;SCA算法在定义的空间区域范围内利用正弦和余弦函数可以平缓地从探索阶段过渡到开发阶段;在优化过程中全局最优解的地点被存储为一个可变目标点而不丢失;在优化过程中，候选解总是在当前最优解周围更新他们的地点，并不断趋向于搜索空间中的最佳区域[11]。

2 多阈值Otsu图像分割

最大类间方差法即Otsu算法的基本原理是采用穷举法选取最佳的阈值组合，将图像按灰度级的不同分成多个部分，使分割后的图像存在最大的类间方差[12-14]。对于一幅图像（大小为M×N）的灰度级为L，图像中各个灰度值为0到L-1。图像中灰度值为i的像素总数为ni，像素总数可以表示为：

N=∑L-1i=0ni。（3）

像素灰度值为i出现的概率为：

pi=niN。（4）

假设要将图像分成n部分，则阈值可以表示为T1，T2……Tn-1，使用n-1个阈值进行图像分割结果可表示为：

G0=（0，1，…，T1）。

G1=（T1+1，T1+2，…，T2）。

……

Gn-1=（Tn-1+1，Tn-1+2…L-1）。（5）

对于这n个部分来说，每部分总像素出现概率是P1，P2，…，Pn-1。其中：

Pk=∑Tk+1i=Tk+1pi。（6）

μk=1Pk∑Tk+1i=Tk+1ipi。（7）

σ2k=∑Tk+1i=Tk+1i-μk2piPk。（8）

图像的灰度均值为：

μ=∑L-1i=0ipi 。（9）

类间方差为

σ2b=∑n-1i=0Pi（μi-μ）2 。（10）

图像的类间方差越大，错分的概率越小，所以使σ2b达到最大的阈值组合即为所求的最佳阈值。

3 SCA改进的Otsu图像分割

为了解决传统多阈值分割中存在的寻优速度慢，易陷入局部最优，抗噪性能差等问题，许多学者引入智能优化算法来寻找合适的阈值组合，如2006年何庆元[15]提出基于粒子群算法的Otsu法图像阈值分割。马文[16]提出基于遗传算法的Otsu法在图像分割中的应用。本文采用正余弦算法对图像分割的阈值选取过程进行优化，在SCA算法中，无论是正弦还是余弦优化，每一代候选解都会与最优解进行信息交流。利用正余弦函数的震荡特性使算法逐步收敛于全局最优，有效避免陷入局部最优，在保证程序运行时间的同时提高了寻优的精度。利用标准测试图像进行实验加以证明。

SCA算法流程如下：

Step1：种群初始化。设种群的群规模为m在[0，255]范围内随机生成m个解，并且随机设定各解的初始位置。

Step2：计算所有解的适应度。 Otsu法的基本原理是根据最大类间方差来选择最佳门限阈值，将计算类间方差的函数作为适应度函数。适应度函数值越大，类间方差越大，图像的分割效果也就越好。

Step3：解的位置的更新。根据r4值选择相应的位置更新公式，更新候选解在每一维度上的位置，重新计算所有候选解的适应度值 ，从而得到每个解的适应度以及本次全局最优位置的适应度。

Step4：比较并更新全局最优解的位置。将更新后的每一个解的适应度值与全局最优解的适应度值进行比较，如果当前解的适应度值大于全局最优的适应值，则更新全局最优解的位置。

Step5：算法终止条件。当最优解的位置在40次迭代均不发生改变时或者达到最大迭代次数时则终止迭代，此时把寻得的最优解在每一维度上的值作为图像分割的最佳阈值。

算法实现流程图如图2所示。

4 图像分割实验与分析

4.1 实验准备

为验证SCA算法在图像分割上具有的优点，本次实验对四幅图像进行阈值分割并将结果进行对比分析，如图3和图4所示，分别展示出原图与其灰度直方图，直方图是通过统计每个灰度级出现的概率来反映图像中灰度分布情况。4幅图像中均存在噪点多，光照不均等问题，若使用传统的阈值分割方法提取目标，难度会明显提高而且准确性会降低。为了证明SCA算法在处理实际问题中的优越性，本次实验对每幅图像分别进行4、6、8、10个这4种类型阈值的分割，并且与基于PSO的图像分割进行对比分析，两种算法分割后的图像如图8所示，分别记录两个算法的寻优时间。

图像质量的评价是一种衡量图像质量好坏的指標。为了对图像分割后的效果进行评价，需记录图像的PSNR和SSIM的值。峰值信噪比（PSNR）[17]是基于图像像素灰度值进行统计和评论计算，是用来衡量图像失真的指标之一，PSNR的值越大，表示图像的失真程度越小。结构相似法（SSIM）[18]是从原始图像的对比度、结构信息以及亮度的角度出发，比较衡量两幅图像相似度的指标，SSIM指标的结果数值范围为0到1，当两幅图像相同时，SSIM 的值等于1。

4.2 结果与分析

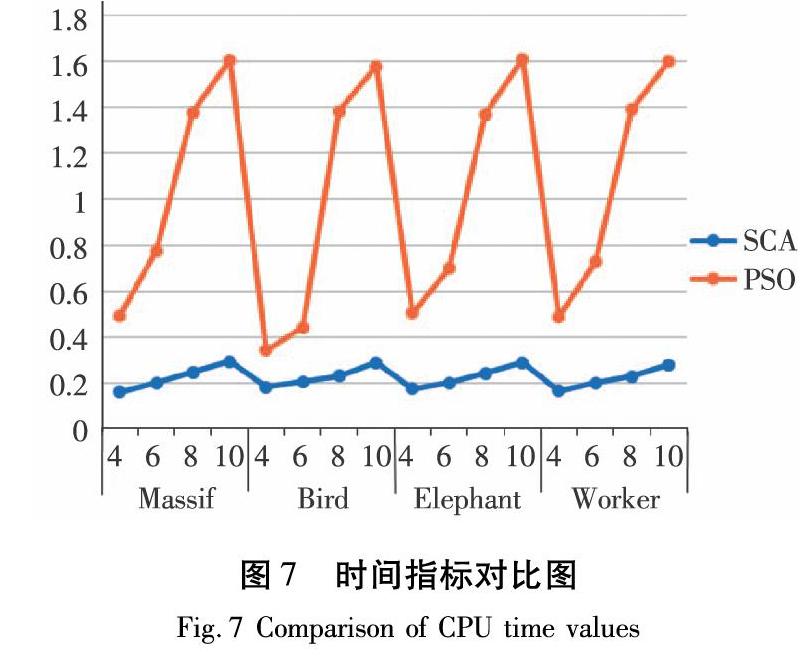
将本文提出的方法与基于PSO优化算法的多阈值图像分割进行对比，记录算法运行的时间、PSNR、SSIM三个指标并利用折线图的方式呈现出来，如图5～图7所示，可以更直观地观察到两个算法在多阈值图像分割中的差异性。进行15次实验，见表1，分别记录三个指标在不同阈值个数下的平均值和标准差，通过对实验数据的分析可知，正余弦优化算法应用在图像分割中具有更好的稳定性。

通过对实验数据的分析，在利用4、6、8、10个阈值进行图像分割时，SCA优化的多阈值图像分割中的PSNR和SSIM值均大于利用PSO算法进行优化得到的值，这说明利用SCA算法寻优后得到的图像的失真程度更小，与原图更加相似，表现出了SCA算法在图像分割多阈值选取问题中的优越性。随着分割阈值个数的增加，图像的层次分布越来越明显，视觉效果也在不断提高。在低阈值时，图像分割效果差异并不明显、数据结果相差也比较小，但在较高阈值时，SCA算法的优势显著增加，而且通过与原图比较可以看出个体区分变的更加明显。而且从两个算法10次运行的平均时间上来看，SCA优化算法在每次个体迭代寻优时速度都要比PSO优化算法更快些，由图7可得，SCA算法的运行效率高，且随着阈值个数的增加，SCA算法与PSO算法的差距越来越大，本文提出的方法优势越来越明显。提高了该算法在图像分割中的寻优效率，同时SCA优化算法借助其随机性，在很大程度上避免了寻优过程中陷入局部最优，影响图像分割的效果。综上所述，从图像的分割效果和数据的对比分析来看，利用SCA算法优化算法进行多阈值图像分割，不仅提高了图像分割的质量，而且大大缩短了寻优时间，从而验证了SCA算法在图像分割问题中的有效性和正确性。

5 结论

本文结合正余弦优化算法来确定最大类间方差法的最佳阈值，通过全局探索和局部开发来寻得最优阈值组合。基于正余弦优化算法的图像分割不仅能较好地改善传统多阈值分割计算量大，消耗时间长的缺点，而且还可以解决在较高阈值时分割效果差以及容易陷入局部最优的问题。实验通过对图像分割中寻优时间、PSNR和SSIM三个指标的分析，表现出正余弦算法应用在图像分割中具有原理简单、参数少和鲁棒性好等优点，与粒子群算法相比，能够获得更好的图像分割质量，可靠性好，有利于图像的后续处理;为多阈值图像分割提供了一种更精准的解决方案。

【参 考 文 献】

[1]李磊.图像分割研究现状概述[J].信息技术与信息化，2015，22（3）：85-87.

LI L. An overview of the research on image segmentation[J]. Information Technology and Informatization， 2015，22（3）： 85-87.

[2]李玲，张旭，贾磊磊.火焰图像分割算法研究[J].科技视界，2015，5（33）：105-106.

LI L， ZHANG X， JIA LL. Research on flame image segmentation algorithm[J]. Science and Technology Horizon， 2015，5（33）：105-106.

[3]刘超，蔡文华，陆玲.图像阈值法分割综述[J].脑知识与技术，2015，11（1）：140-142.

LIU C， CAI W H， LU L. An overview of image segmentation threshold method[J]. Brain Knowledge and Technology， 2015， 11（1）：140-142.

[4]申铉京，潘红，陈海鹏.基于一维Otsu的多阈值医学图像分割算法[J].吉林大学学报，2016，54（2）：344-348.

SHEN X J， PAN H， CHEN H P. Muti-threshold medical image segmentation algorithm based on one-dimensional otsu[J]. Journal of Jilin University， 2016， 54（2）：344-348.

[5]程玉柱，蔡云飞.基于分数阶CV模型的木材缺陷图像分割算法[J].林业机械与木工设备，2018，46（4）：44-47.

CHENG Y Z， CAI Y F. Wood defect image segmentation algorithm based on fractional order CV model[J]. Forestry and Woodworking Equipment，2018，46（4）：44-47.

[6]陈峥，石勇鹏，吉书鹏.一种改进的Otsu图像阈值分割算法[J].激光与红外，2012，42（5）：584-588.

Chen Z， Shi Y P， Ji S P. An improved threshold Segmentation for otsu images [J]. Laser and Infrared，2012，42（5）：584-588.

[7]吴军，王龙龙.基于双鸟群混沌优化的otsu图像分割算法[J].微电子学与计算机，2018，35（12）：119-124.

WU J， WANG L L. Otsu image segmentation algorithm based on double Bird Group chaos optimization[J]. Microelectronics and Computer， 2018，35（12）： 119-124.

[8]赵乃刚，邓景順.粒子群优化算法综述[J].科技创新导报，2015，12（26）：216-217.

ZHAO N G， DENG J S. An overview of particle swarm optimization algorithm[J]. Scientific and Technological Innovation Guide， 2015， 12（26）：216-217.

[9]李海楠，张学良.基于群体适应度方差的粒子群优化算法[J].计算机仿真，2007，24（5）：158-161.

LI H N， ZHANG X L. Particle swarm optimization algorithm based on variance of population fitness[J]. Computer Simulation， 2007， 24（5）：158-161.

[10]MIRJALILI S. SCA：a sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems， 2016， 96：120-133.

[11]刘勇，马良.转换参数非线性递减的正弦余弦算法[J].计算机工程与应用，2017，53（2）：1-5.

LIU Y， MA L. A sinusoidal cosine algorithm for nonlinear decrement of transfer parameters[J]. Computer Engineering and Application， 2017， 53（2）：1-5.

[12]孙俊，宋佳，武小红.基于改进Otsu算法的生菜叶片图像分割方法[J].江苏大学学报，2018，39（2）：179-184.

SUN J， SONG J， WU X H. Segmentation of raw vegetable leaf image based on improved otsu algorithm[J]. Journal of Jiangsu University， 2018， 39（2）：179-184.

[13]王裔，段会川.Otsu方法在多阈值图像分割中的应用[J].计算机工程与设计，2008，29（11）：2844-2845.

WANG Y， DUAN H C. Application of otsu method in multi-threshold image segmentation[J]. Computer Engineering and Design， 2008， 29（11）：2844-2845.

[14]OTSU N. A threshold selection method from gray-level histogram[J]. IEEE Transactions on System， Man， and Cybemetics， 1979， 9（1）：62-66.

[15]何庆元，韩传久.基于粒子群算法的Otsu法图像阈值分割[J].桂林电子科技大学学报，2006，26（5）：355-358.

HE Q Y， HAN C J. Application of otsu method based on particle swarm optimization in image segmentation[J]. Journal of Guilin University of Electronic Science and Technology， 2006，26（5）：355-358.

[16]马文，周绍光，丁慧珍.基于遗传算法的Otsu法在图像分割中的应用[J].沿海企业与科技，2005，10（8）：160-161.

MA W， ZHOU S G， DING H Z. Application of otsu method based on genetic algorithm in image segmentation[J]. Coastal Enterprises and Science and Technology， 2005，10（8）：160-161.

[17]SHEIKH H R， SABIR M F， BOVIK A C. A statistical evaluation of recent full reference image quality assessment algorithms[J]. IEEE Transactions on Image Processing， 2006， 15（11）：3441-3452.

[18]WANG Z， BOVIK A C， SHEIKH H R， et al. Image quality assessment： from error visibility to structural similarity[J]. IEEE transactions on image processing， 2004， 13（4）：600-612.