温度与压力场作用下枪管耦合场分析

2019-06-07薛洪彬

沈阳理工大学学报 2019年6期

郭创,杨丽,2,薛洪彬

(1.沈阳理工大学装备工程学院，沈阳110159；2.重庆建设工业(集团)有限责任公司，重庆 401300；3.重庆红宇精密工业有限责任公司,重庆402760)

自动武器射击时，通过机械作用将底火引发，随后迅速点燃发射药。火药点然后释放大量的气体和能量；火药燃气瞬间膨胀，产生高温和高压，使得弹丸快速的沿着枪管内膛向前运动。这个过程中枪管内火药燃气混合气体温度超过2500K，压力超过250MPa。连续射击时，内膛长时间处在高温高压环境中，表面金属有可能出现融化现象，同时，火药燃气混合气体产生的巨大压力会对铬层表面产生烧蚀磨损，烧蚀磨损的存在大大缩短了枪管的使用寿命。在物理与化学破坏的共同作用下，枪管铬层将发生烧蚀磨损和破坏。随着枪管内壁破坏的不断加剧，其弹道性能将会受到严重影响，如射击精度、弹丸初速、横弹率等。如果发生严重烧蚀磨损未及时发现，将会导致使用时枪管发生破裂，严重影响武器使用者的安全[1]。因此,研究单发、连续射击时，温度和膛压共同作用下枪管耦合场的变化规律非常重要,王菲等[2]，运用 ANSYS软件建立了枪管二维轴对称有限元模型，确定枪管的边界条件，得到了单发时枪管的温度分布和连发时的温度及应力分布。顾祖成等[3]利用 ANSYS 软件建立某小口径自动步枪身管有限元模型，对身管内外壁的对流传热和身管壁内的热传导进行仿真，计算求解得到了不同射击模式及不同环境温度下身管内外壁温度的变化规律，结果表明，射速增大、环境温度越高，身管温度上升越快。

本文以某机枪为例,采用有限元分析法，对枪管在单发、连续发射过程中，温度和膛压共同作用下，枪管耦合场进行数值分析；将数值计算结果与试验数据进行比较，为枪管的设计提供参考。

1 温度场、应力场主要参数的确立

1.1 枪管受热过程

首先是火药燃气对枪管壁的加热：火药燃气以紊流流动方式在枪管轴线上流动，其特点是火药燃气混合气体在膛内以螺旋状运动，故火药燃气的混合气体是以对流放热方式向内壁传热的。其次，枪管铬层向钢层传热：武器在连续发射时，枪管内壁需承受周期性的剧烈温度变化，热量不断由枪内膛铬层向枪管钢层外壁传递，枪管外壁与自然环境进行热交换。当外壁与自然环境产生足够大温差时，会发生大气自然对流换热情况[4]。

1.2 边界条件的确定

火药燃气的混合气体温度及放热系数决定武器枪管温度场和应力场的求解，准确计算这两个参数对求解计算影响很大[5]。

1.2.1 火药燃气温度历程

火药燃气混合气体温度历程共有两个阶段，分别是内弹道期和后效期。内弹道期：弹丸点火发射、火药燃气温度从环境温度快速上升至爆温；后效期：弹丸从枪口射出后，残留火药燃气混合气体继续向枪管内壁传递热量。

第一阶段火药燃气温度为

Tg(t)=[1-(k-1)φqv(t)2/(2fωψ)]Tbw

(1)

式中：v(t)为弹丸在枪管膛内稳定运动的速度；q为弹丸在膛内运动时的质量;ω为弹丸发射时装药量；k为绝热系数；φ为虚拟系数；ψ为火药燃去部分的百分比；Tbw为火药燃气混合气体爆温；f为火药力；t为内弹道期的时间。

第二阶段火药燃气温度为

Tg(t)=Tbwe-AtB

(2)

式中：A、B为拟合指数，B=ln[ln(TK/Tbw)/ln(Ta/Tbw)]/ln[tndd/tndd+thxq]

式中：Tk为内弹道结束时枪管中火药燃气和空气混合气体的平均温度；Ta为后效期终止时膛内火药燃气和空气混合气体的平均温度；tndd为内弹道存在的时间；thxq为枪管内膛后效持续时间[6]。

1.2.2 火药燃气的放热系数

自动武器射击时,火药燃气混合气体瞬间达到较高温度与枪管内壁产生巨大的温差，发生热交换。火药燃气混合气体与枪管内膛铬层以强迫对流换热的方式进行热交换[7]。

弹丸发射期间，放热系数根据热力学相关原理进行计算。

(3)

由式(3)可得

h(x,t)=0.023Kg(t)/d[Vg(t)ρg(t)d/μg(t)]×[Cpg(t)μg(t)/Kg(t)]0.4Kc

(4)

式中：Re为雷诺数；Pr为普朗特数；Vg(t)、Kg(t) 、ρg(t) 、μg(t) 、Cpg(t)分别为火药燃气在膛内的运动速度、热导率、密度、动力粘度和比热容；Kc为热辐射更正系数，取值为1.15～1.2[8]。

枪管后效期火药燃气混合气体放热系数为

h(x,t)=0.002[V*dρg(t)/2μg(t)]×ρg(t)V*/2cpg(t)

(5)

1.2.3 自然对流系数

连续射击时，火药燃气混合气体产生的热量不断传递给枪管内壁，然后由枪管内壁铬层传向钢层外壁。随着时间推移，热量不断传递，外壁温度不断地升高，与周围环境存在一定温差，由于温差的存在，自然对流换热将产生。自然对流换热也发生在连续射击间隙。自然对流换热系数为

α1=0.54(GrPr)1/4λ/d

(6)

式中：Gr=βΔTd3/V2，为Grashof数；β=1/(T+273)，为空气容积膨胀系数；T=(T0+Tb) 为定性温度；T0为293K；Tb为武器枪管外壁温度；T为枪管开始冷却时外壁与环境的温度差值；V为空气动黏度；λ为空气热导率；d为枪管外径；Pr为普朗特数。

2 数值模拟方案

2.1 有限元模型的建立

考虑枪管工作时的状态和受力情况，将机枪枪管简化为二维轴对称模型。

2.2 材料模型设置

铬层和钢的材料参数如表1所示。

表1 材料性能与物理参数

2.3 边界条件

(1)火药燃气的压力历程如图1所示。

图1 火药燃气压力-时间曲线

由图1可以看出，枪管在短时间充满大量气体，产生巨大压力；内膛火药燃气压力先迅速升高，在0.001s时达到峰值，为430MPa，然后缓慢下降。

(2)火药燃气温度历程如图2所示。

由图2可知，火药燃气温度开始时达到2700K，随后不断下降，直到接近室温。

图2 火药燃气温度-时间曲线

(3)火药燃气放热系数如图3所示。

图3显示，火药燃气放热系数在0.001s时达到峰值，为17200Wm2K-1，此时火药燃气向内膛传递热量速度最快。

2.4 仿真结果

2.4.1 温度场分析

将温度载荷施加于枪管内膛,进行温度场的求解。温度场计算结果如图4～图7所示。

图3 火药燃气放热系数-时间曲线

图4 单发时铬层温度-时间曲线

图5 单发时钢层温度-时间曲线

图4为单发射击时，铬层在极短时间内达到最高温度750K，然后不断衰减直至室温；图5的基体钢层在0.04s时到达到最高温度340K，枪管内壁铬层温度高于钢层温度。铬层表面温度迅速升高，是由于火药燃气在很短时间内加热铬层，又因为热量无法在铬层内快速传播，致使热量大量堆积在枪管铬层表面，使枪管铬层表面温度快速升高。随着热量不断地传递，钢层温度也逐渐开始升高，枪管内部温度分布不均的程度开始减少。

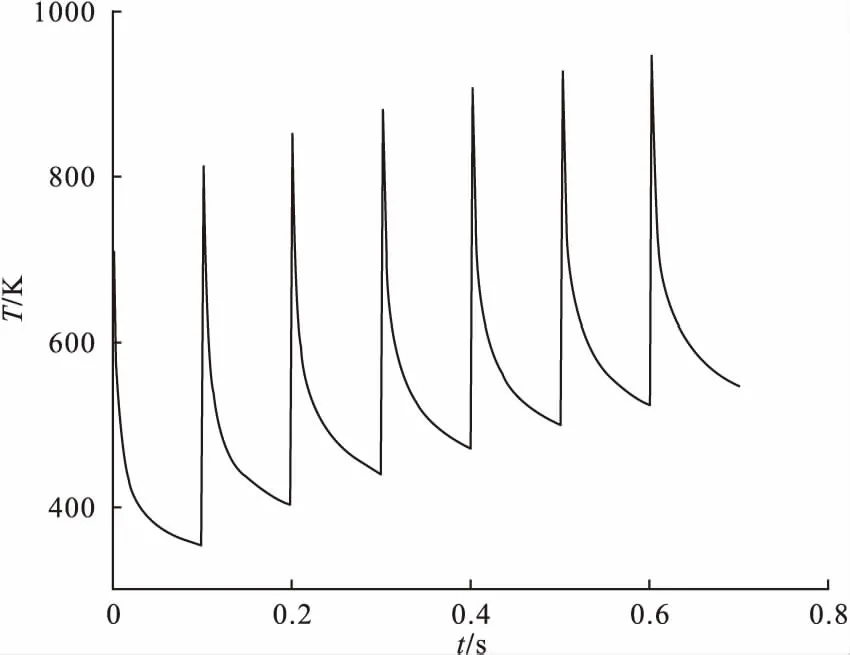
图6 连发时铬层温度-时间曲线

图7 连发时钢层温度-时间曲线

图6为连发时，铬层在0.6s时达到最高温度930K；图7为基体钢层温度0.6s达到450K，远远小于铬层温度。铬层温度呈现规则的周期性变化规律，其频率与射弹频率相同。随着射弹数的增加，脉冲峰温度呈现先迅速的增加，随后逐步趋缓，脉冲振幅逐渐减小，但内膛表面温度大幅增加，剧烈变化的区域主要集中在铬层表面。根据热力学公式可知，枪管吸收热量的多少取决于枪管内火药燃气与铬层温差的大小，即温差越大铬层吸收的热量就越多。连续射击时，由于铬层不断吸收热量，使得温度不断地上升，同时铬层与火药燃气的温差不断地减少，导致铬层吸收的热量不断减少，表现为铬层温度峰值增幅趋缓。温度是影响烧蚀的主要原因，控制内膛温度可以减缓内膛烧蚀。有关研究表明[9]：枪管烧蚀量的大小与枪管内膛最高温度有直接关系。

2.4.2应力场分析

施加温度载荷和膛压载荷于模型上，进行应力求解。结果如图8～图11所示。

图8 单发时铬层表面应力-时间曲线

图9 单发时钢层应力-时间曲线

图8为单发时铬层最大应力600MPa；图9为钢层最大应力460MPa。应力特点是先上升，然后下降。由铬层到钢层，应力峰值迅速减小，钢层应力峰值小于铬层应力峰值，使得铬层有效的保护了钢层。

由图10可知，连续射击时，铬层应力呈现先上升后下降的规律。铬层表面是应力集中的区域，即枪管内膛表面。通过图10图11可知，在枪管连续射击情况下，铬层和钢层最高应力分别为1200MPa和1000MPa，由于弹丸发射间隔较短，膛内热量还未消散，下一发弹丸又开始射击，导致内膛的温度持续上升，使得枪管的热应力也持续上升，进而影响耦合应力的峰值持续增加，直至达到内外温度平衡，耦合应力停止增加。枪管铬层应力很大，且沿枪管径向(铬层到钢层)逐渐衰减，这种循环应力是枪管产生裂纹的直接诱因。在连续射击过程中，产生的裂纹会逐渐贯通，形成烧蚀坑，进而造成更大的烧蚀磨损。