微球聚焦测井仪推靠系统运动及动力性能

任 涛，冯 斌,2，张 飞，孙 文

(1.西安石油大学 机械工程学院，陕西 西安 710065；2.西安华燕航空仪表有限公司，陕西 西安 710000)

0 引 言

微球聚焦测井仪是石油测井领域内一种十分重要的测井设备。微球推靠系统是安装在测井仪上，辅助微球测井仪完成井下测井任务的辅助测井设备[1]。其作用机理如下：微球推靠系统通过电机驱动，可在井下实现推靠臂的张开动作，将安装在推靠极板上的微球测试极板推送至贴靠井壁位置，并与井壁保持有一定的推靠力，以实现对地层井况参数的有效采集。测井完成后，推靠系统在电机驱动作用下，可以实现推靠臂的收拢闭合，使微球测井极板脱离井壁，并贴靠推靠主体保持聚拢状态，以便保证测井仪器整体的上提回收。

近年来，国内针对测井仪推靠系统开展的理论与实践研究较多，像杨柏青对单臂推靠器的力学性能进行了探讨分析[2]。通过对推靠器进行受力分析，对影响推靠器的各因素进行分析并对其存在的理论关系进行研究，为设计出可靠的推靠系统建立了理论依据。受限于当时的技术条件，其仅仅从静力分析出发，未考虑推靠系统的动力参数，因此具有较大的局限性。王会来等关于新型测井仪推靠装置的设计和分析[3]；纪新福关于推靠器中多功能连杆机构的设计及应用[4]；赵斌基于MATLAB的VSP测井仪推靠机构的优化设计[5]；邢家乐，刘立等应用ADAMS运动仿真平台，进行了对新型VSP仪器推靠机构的仿真与优化等；取得了丰硕的成果[6]。

上述大多是偏向于工程应用方面的研究，并且受限于当时的技术背景，并未建立系统的理论分析及优化模型，因而无法保证推靠系统的性能优越性及工作稳定性。无法准确描述测井推靠系统的运动规律和真实的运动状态，而推靠系统极板运动性能的好坏与测井数据的准确性密切相关。调研发现针对测井推靠系统机构运动平稳性，机构初始传动角，极板推靠力以及推靠系统整体的结构参数优化方面的系统性研究与工程实践还不多见。根据新时代背景下的油田测井作业要求，并且从提高测井结果的可靠性，提高测井仪器工作的有效性、减少设备的运营及维修成本、提高测井数据的准确性、稳定性方面来说，有必要从推靠系统机构运动平稳性，机构初始传动角，极板推靠力以及推靠系统整体的结构参数优化方面入手，进行深入的研究。

1 微球聚焦测井推靠系统结构模型

微球聚焦测井仪推靠系统主要机构组成如图1所示。由电机带动丝杠转动，丝杠螺母副推动推力棒水平移动，推力棒上的连接杆连接推力棒与链接臂，将丝杠螺母副的直线运动传递给链接臂转化为复合运动，链接臂推动推靠内臂转动，推靠内臂带动推靠极板、推靠上臂运动，推靠极板运动到位后，通过行程限位开关控制传动系统自锁装置实施自锁，电机停转。储能弹簧作为极板辅助控制机构，在电机运转过程中进行储能，电机停机后，通过储能弹簧来控制推靠极板的微调以规避井下岩壁的磕损。

图1 微球聚焦测井仪推靠系统结构模型Fig.1 Structure model of push system for microsphere focusing logging tool1 电机 2 联轴器 3 丝杠 4 套筒 5 丝杠螺母 6 传动系统自锁装置 7 向心球轴承组 8 推力棒 9 中接头 10 密封螺钉 11 支撑套 12 压力帽 13 套环 14 连接杆 15 链接臂 16 推靠上臂 17 推靠极板 18 极板滑槽 19 推靠内臂 20 储能弹簧 21 止推块 22 推靠主体

2 推靠系统运动学分析

推靠传动装置在任意时刻的位置如图2所示。利用矩阵解析法对机构进行运动分析，根据图示列出机构的封闭矢量位置方程。

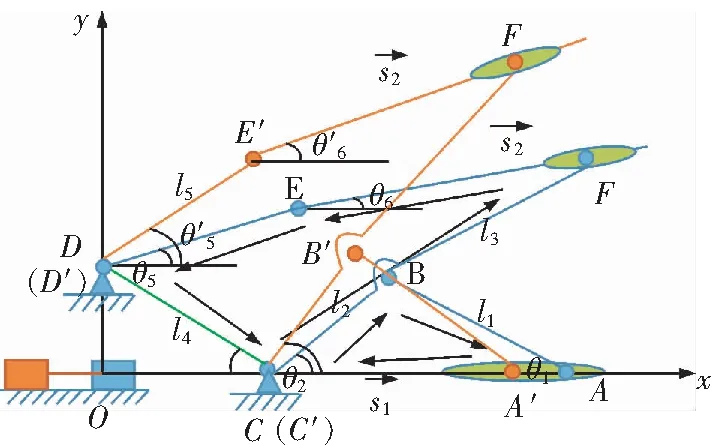
图2 推靠系统运动状态Fig.2 Motion state diagram of push-back system

2.1 系统的位置方程

如图2所示，各杆长矢量及角度位置参数如图中标注，这样就形成由各杆矢量组成的2个封闭矢量多边形[7-9]。即封闭矢量三角形CBAC和封闭矢量四边形FEDCF.

由矢量封闭三角形CBAC可得封闭矢量方程式

(1)

将式封闭矢量方程式(1)写成在坐标上的投影式，即得

(2)

式中s1，l1，l2均为已知量；θ1，θ2为未知量。

在封闭矢量四边形FEDCF中，可列出如下封闭矢量方程式

(3)

将式封闭矢量方程式(3)写成在坐标上的投影式，即得

(4)

式中l3,l4,l5,θ2,θ4为已知量；s2,θ5,θ6为未知量。

2.2 运动分解矢量方程

在微球推靠系统传动机构中存在A，F两处柱销滑槽副，使得固定尺寸参数的七杆机构在运动过程中存在变尺寸参数杆EF，成为变参数七杆机构[10]。微球聚焦测井仪的测试对象是裸眼井，井臂经初始钻挖后未作任何处理，因此井壁粗糙并且局部区域可能会出现坑洞或者垮塌的现象，造成测井仪在井下作业过程中的目标测试位置会根据井壁结构的变化而产生突变[11]。从而造成推靠系统的整体运动规律发生变化具有了不确定性。对此，为分析方便，实现这些不确定性问题的确定解，需要对运动过程进行分解，根据不同过程中的运动特性及其相应的约束状态，可以对某些参数进行固定，从而得到未知参数的确定解[12]。分析过程如下：

2.2.1 起始位置

起始位置推靠系统运动状态如图3所示。

从图3可以看出，在初始时刻，由于推靠传动系统自身结构的特殊性，推靠上臂与推靠极板可看作一个连杆绕D点转动，其初始位置与测井仪轴心线平行。此时推靠内臂、推靠上臂以及推靠极板的运动规律等同于导杆机构[13-14]。

根据前面的分析，在矢量三角形ACBA中可得如下方程式

(5)

其投影式如下

(6)

式中l1，l2均为已知量；s1-0，θ1-0，θ2-0为未知量；s1-0为初始时刻柱销滑槽副A距固定铰接C的长度,mm；θ1-0为初始时刻链接臂AB与x方向的夹角，(°)；θ2-0为初始时刻推靠内臂CBF与x方向的夹角，(°)。

回到封闭矢量三角形△CDF中，可得封闭矢量方程式

(7)

将封闭矢量方程式沿坐标方向投影可得

(8)

此时θ5-0=0，则s2-0=l4cos(θ4)+l3cos(θ2-0).

式中s2-0为初始时刻柱销滑槽副F距固定铰接E的长度,mm；θ5-0为初始时刻推靠上臂DE与x方向的夹角,(°)。

2.2.2 中间过渡阶段

图4为推靠系统机构运动到第一运动状态末时刻的位置图示。从初始时刻到第一运动状态末过程中，推靠上臂与推靠极板作为一个整体可以看作一个连杆绕D点转动[15]。

图4 推靠系统运动状态(第一运动状态末)Fig.4 Motion state diagram of push-back system (The end of the first state of motion)

从图4可以看出，在中间过渡阶段，测井推靠极板上触头接触井壁，形成新的支点，导致推靠上臂与推靠极板的运动状态发生变化，推靠上臂沿D点转动，推靠极板在井壁约束下作平面运动。此时推靠内臂、上臂以及推靠极板的运动规律等同于双摇杆机构[16-17]。其中R0表示测试井径的半径。根据封闭矢量多边形FDCF，可列出如下封闭矢量方程

(9)

将其沿坐标方向投影可得

(10)

式中l3，l4，l5，θ2-1，θ4，θ5-1为已知量；s2-1为未知量；s2-1为第一运动状态过程中柱销滑槽副F距固定铰接E的长度，mm；θ2-1为第一运动状态过程中推靠内臂CF与x方向的夹角,(°)；θ5-1为第一运动状态过程中推靠上臂DE与x方向的夹角,(°)。

2.2.3 终止位置

图5为推靠系统的终止时刻的位置图示。从第一运动状态末到终止位置过程中这里称之为第二阶段运动状态。

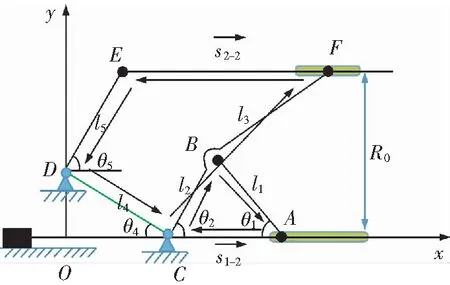
图5 推靠系统运动状态(第二运动状态末)Fig.5 Motion state diagram of push-back system (The end of the second state of motion)

从图5可以看出，推靠极板与井壁贴合并保持与测井仪轴心线平行[18]。根据封闭矢量多边形FEDCF，可列出如下封闭矢量方程

(11)

将其沿坐标方向投影可得

(12)

式中l3，l4，l5，θ2-2，θ4，θ5-2为已知量；s2-2为未知量；s2-2为第二运动状态过程中柱销滑槽副F距固定铰接E的长度，mm；θ2-2为第二运动状态过程中推靠内臂CF与x方向的夹角,(°)；θ5-2为第二运动状态过程中推靠上臂DE与x方向的夹角,(°)。

从第一运动状态末到第二运动状态末过程中s2，θ5的连续变化可通过下式求得

(13)

从式(13)可得

(14)

3 动态静力分析

对推靠系统主要杆件进行受力分析，其受力情况如图6～8所示，分别以各杆件为研究对象建立力平衡方程[19-20]。

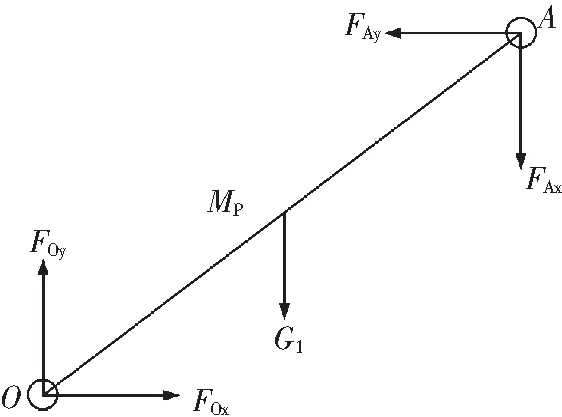
图6 推靠上臂OA的受力分析Fig.6 Force analysis of push arm OA

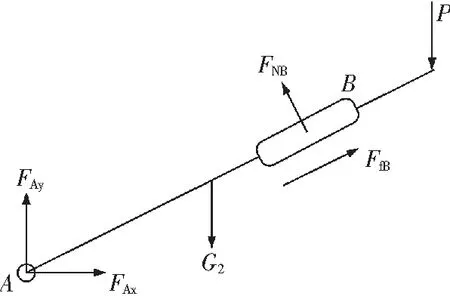
图7 推靠极板AB的受力分析Fig.7 Force analysis of pushing plate AB

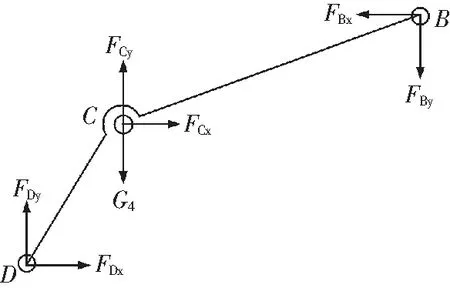
图8 推靠内臂BCD受力分析Fig.8 Force analysis of BCD pushing the inner arm

1)取推靠上臂OA为研究对象。分析推靠上臂OA的受力，根据受力分析情况列出如下力平衡方程。

∑MO→FAxyA-FAyxA-G1x1=0

2)取推靠极板AB为研究对象。

3)取推靠内臂BCD为研究对象。

4 实例分析

推靠系统中各杆件尺寸参数如下：链接臂80 mm，推靠内臂短节46 mm，推靠内臂375 mm，推靠内臂固定铰接点到推靠上臂固定铰接点距离96 mm，推靠上臂279.4 mm，推靠极板294 mm，推靠上臂铰接点距测井仪轴心线的竖直距离36.4 mm，裸眼井井径8.5 in(25.4*8.5 mm)。

推靠极板质心点位移、速度、加速度曲线如图9所示，推靠系统在机构张开过程中推靠极板的推靠力曲线及主传动机构传动角曲线如图10，11所示。

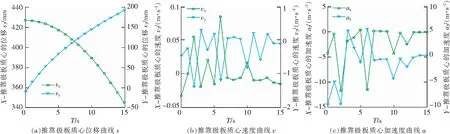
图9 推靠极板质心运动曲线Fig.9 Moving curve of centroid of polar plate

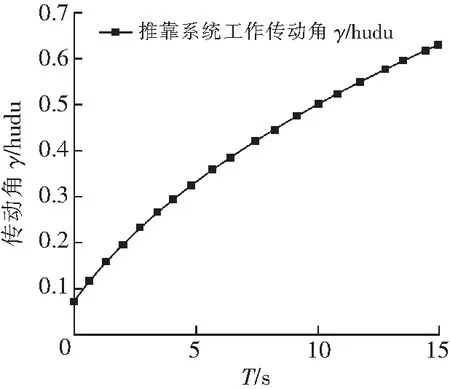
图10 推靠系统传动过程中主传动机构传动角曲线Fig.10 Driving angle curve of main transmission mechanism in the course of driving system

图11 推靠系统传动过程中推靠极板的推靠力Fig.11 Pushing force of the pole plate in the driving process of the push system

5 仿 真

5.1 推靠系统仿真模型

微球聚焦测井仪推靠系统动力学虚拟样机模型如图12所示。推靠系统是贯穿在测井仪器串中下入井内，仪器通过分布在测井仪各段的扶正器扶正，将测井仪的中轴线保持在井径中心位置。当测井仪下放到目标测试段时，通过人为控制电机作用，使得推靠系统开始工作。由于该测井仪器测试对象为裸眼井，井内岩壁未作处理，因此井内局部区域可能会存在坑、洼区块，从而造成区域井径的突变。从而就给推靠系统带来了不确定外部井径约束[21-22]。除此之外，主要约束有柱销滑槽副A在推靠主体上的移动副、柱销滑槽副F在推靠极板滑槽上的移动副，丝杠螺母的螺旋副与圆柱副以及各连接处的铰接副。

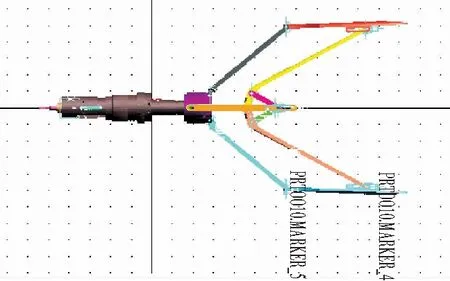
图12 微球聚焦测井仪推靠系统动力学分析模型Fig.12 Dynamic analysis model of push-system for microsphere focusing logging tool

5.2 推靠系统运动及动力学仿真

5.2.1 推靠极板位移，速度，加速度仿真曲线

经过虚拟仿真求解，微球推靠极板的运动仿真曲线如图13～15所示。

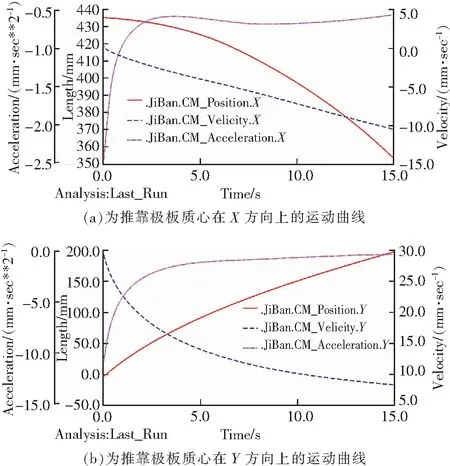
图13 推靠极板质心方向运动曲线Fig.13 Moving curve of center of mass of polar plate

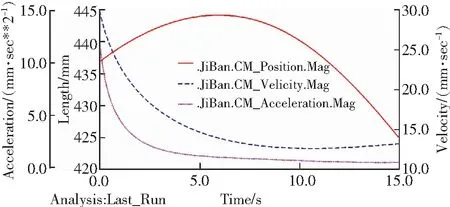
图14 推靠极板质心综合运动曲线Fig.14 Comprehensive motion curve of centroid of polar plate

图15 推靠极板上铰接点F处滑槽副的运动曲线Fig.15 Motion curve of hinge point F on pushing plate

5.2.2 分析讨论

对比实例分析获取的推靠极板运动规律曲线图9与虚拟仿真模拟所得到的推靠极板运动曲线图13～15可以发现推靠系统的位移轨迹曲线基本拟合，推靠系统的速度及加速度曲线两者的分析结果有较大差别。理论分析的结果基本符合虚拟仿真结果，能够正确反映出实际的运动轨迹与趋势，但是在推靠极板度速度及加速度的线连续性方面，理论分析存在一些不足，没有虚拟仿真结果平滑，对于造成数理分析曲线与模拟仿真差别的原因，这里分析有以下4个方面。一是由于在数理建模过程中，为分析方便将滚珠丝杠螺母用滑块替代(将其旋转推进作用直接用滑块的水平移动来替代)、柱销滑槽副用铰接点替代；二是在数理模型分析过程中，对于推靠系统的实际井下约束工况是无法保障的，而在物理仿真模拟过程中，则是按照真实的结构原型以及真实的工况约束进行实际的工作拟合；三是由于仿真模拟是连续的过程，而数理模型的求解是通过过程阶段分析，通过分段点的参数固定来求解各杆件参数关系，相对于方仿真模拟的连续过程，这里的分析是离散化的；四是仿真曲线中的速度、加速度是在软件自带的内置函数多次迭代下取得的，已对曲线进行了光滑处理，而实际的数理模型分析则是在推靠系统的全运动周期中截断选取，参照有限元分析的微元法，保证在所取的节段上满足可导，连续，然后进行曲线的整合分析输出的结果。因此，两者输出的结果在曲线上存在一定的区别度。

6 结 论

1)对比数理分析与仿真模拟曲线可以发现，抛开曲线的连续性及光滑度，单从推靠系统速度及加速度曲线的数值上分析，实例分析结果以及仿真结果有着相似的规律。首先从运动起始点开始，0～5 s的时段内，仿真与数理分析的加速度曲线具有相似的变化趋势，加速度曲线的跳动持续时间更长，幅度更大。但是，经过这一时段之后，其加速度无论是数理分析结果亦或是虚拟仿真结果，都在围绕0基准线进行靠拢。满足推靠系统的实际工作情况。所以从整体轨迹轮廓上来看，两者的结果是相互拟合的，验证了推靠系统数理模型的合理性。

2)从推靠极板的运动特性仿真曲线中可以发现，其速度在整个运动过程是稳步增加的，加速度也没有大的跳动。而在数理模型的分析结果中，极板的速度，加速度都有较大的冲击与跳动。说明柱销滑槽副的连接方式，改善了推靠极板与井壁的贴靠过程，使得极板在整个推靠过程速度，加速度能够保持平稳，减小了极板贴靠井壁的刚性接触为推靠系统带来的冲击与振动，延长了推靠系统的工作寿命，也保证了推靠系统的运动平稳性。证明了柱销滑槽副对推靠系统运动状态改善的有效性。

3)在推靠系统的工作行程内，传动角处于持续增大过程，但是初始传动角较小，并且传动角增速较慢，不利于推靠系统的力学性能传递。推靠极板的推靠力在0～10 s维稳在较小的范围内，在10～15 s突变，这对于推靠系统的运动平稳性来说具有一定的冲击，不利于推靠系统平稳的工作。并且通过浮标点发现推靠极板在贴合井壁时推靠力在211.9 N(期望推靠力240 N)，未到达实际测井要求，从而可能导致安置于推靠极板上的微球极板不能紧密的贴合井壁，造成测井数据的失真，导致测井作业失效。因此，需要对推靠系统传动机构进行结构改进、优化处理，以改善其工作性能，保障测井准确性。