平面电磁波极化场矢量的时空机理

2019-06-06田一涵

西安科技大学学报 2019年3期

田超，田一涵

(1.西安交通大学城市学院，陕西西安 710018；2.西安科技大学通信与信息工程学院，陕西西安 710054)

0 引言

均匀平面电磁波是电磁波理论分析、工程实践中应用得最多的。无线通信、遥控、遥测等信息工程技术中，凭借平面电磁波传递信息，它是整个系统中的重要环节。电磁波不同的极化方式，其时空关系不同，决定了电磁波的不同性质，在电磁波发射、接收的过程中作用不同，这些重要的物理关系，在如天线工程技术中尤为重要。对极化作用的定义，电磁波场量的时空分布，运动方式，这些较复杂抽象的时空关系，建立正确清晰的概念，是诸多信息、通信、遥控遥测等工程实践中充分发挥电磁波功能的前提。笔者查阅了上世纪40年代至今，70多年数十种重要的国内外文献，多是在电磁波前进方向的一个垂直截面上，分析并定义了线极化、圆极化以及圆极化的旋向，而对于电磁波场量在时间上、空间上的分布相互关系，电磁波运动方式究竟如何，则未见到进一步深入分析讨论的相关论述。极化场矢量的时空关系，线极化和圆极化具有代表性，它们的场矢量在时间上在空间中分布如何，随着时间推移如何运动，圆极化旋向的时空关系，都是电磁波运动的基本性质，这些重要的概念，理应厘清，这是分析研究的一个重点。同样也着重指出，电磁场是一种物质，这种物质以不同的大小和方向，从发射装置中发射出来，形成电磁波的强度和极化方向。以均匀平面电磁波为例，波一经形成之后，就始终保持着原来的不变的形状、大小和方向，在无耗均匀媒质中运动。电磁波作为物质波，波的运动即形成这种波的物质的运动。声波、水波与电磁波，有着表面相似的方程，但声波、水波是介质粒子在各自平衡位置附近的纵向或横向振动形成的表象，介质是不随波一同前进的，在这点上电磁波与声波、水波有着本质上的完全不同。电磁波的波动方程E(r)=Emsin(ωt-βz)ax及其物质性的性质，体现了电磁波的本质特征，通过对方程及其参数的认真分析及计算，是建立正确的电磁波时空科学概念的重要且可靠的方法。

1 线极化电磁波

1.1 线极化正弦电磁波分析

正弦电磁波的线极化分析。在各向同性、线性、均匀介质中，均匀平面电磁波是横向电磁波(TEM波)。由于电、磁场量有确定关系，这里仅就电场矢量来分析[1-3]。设电磁波中电场强度矢量为

E(z,t)=Ey(z,t)ay=Emsin(ωt-βz)ay

(1)

即电磁波沿z方向前进，矢量E(z,t)指向y轴方向，随时间按正弦变化的波幅值Em为定值。式(1)表明，在任意某z处，垂直z的波阵面上所有点上，在任意t时刻，场矢量E(z,t)均有相同大小和方向[4]。

任取t=t1时刻，场量仅是z的变量的正弦函数，矢量E(z,t)的矢端轨迹是一条处于yz平面上的正弦曲线。此时，任一点z的场量的大小，由该点相位φ1如式(2)所示的决定

φ1=(ωt1-βz)

(2)

取电磁波上任一点z=z1，此处相位为

φ11=(ωt1-βz1)

(3)

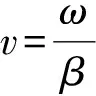
φ22=(ωt2-βz2)

(4)

将t2=t1+Δt，z2=z1+Δz两式代入式(4)有

φ22=(ωt1-βz1)+(ωΔt-βΔz)

(5)

因为

(6)

可得

φ22=(ωt1-βz1)=φ11

(7)

因为t1，z1是在正弦电磁波上任意取的，式(7)表明了一个重要结论，就是线极化电磁波上，任何一点在整个运动过程中，相位始终不变[5-7]。由式(1)可见，上述结论保证了电磁波场矢量在电磁波运动时其值大小不变，而电场矢量E(z,t)的方向是不变的，这样，线极化电磁波的所有电场矢量，在电磁波直线运动的全过程中，始终保持着各自的大小、方向不变，沿着波前进方向的所有平行直线上，全部场矢量，自始至终一直保持着不变的正弦分布状态，在yz平面中以相速v前进[8-11]。正弦波形的所有部分，均没有随时间自身上下起伏波动的情况。

1.2 电磁场量、功率流、能量关系

取在某个z处垂直于波前进方向的平面上，当电磁波经过时，观察到随时间推移形状不变的正弦分布着的所有场矢量，次第经过平面，在y方向上产生一个随时间变化的时变正弦场量，并在垂直平面(xoy平面)上划出一条长为2Em，y方向上的直线段轨迹，这正是线极化名称的由来[12-15]。

平面电磁波推进的过程中，空间连续分布的正弦场量，进入介质时，随时间推移，介质各点，不断感受着时变正弦电磁场[16-17]；若电磁波进入导体或天线，则在其中各点产生相应频率时变电磁场引起的电流等相关的电磁变化[18-21]。在某个z处出现的时频电磁场既不是某一个场矢量单独随时间作正弦变化形成的，也不是自身随时间上下起伏波动的系列场量所致。在真空中行进的平面电磁波，其所有场矢量都保持着自身的大小及方向前进;在介质或导体中则引起随时间变化如极化、衰减等情况，这才是事实的真相。

以上讨论是就电磁场强度矢量而言，根据麦克斯韦方程

(8)

将式(1)代入式(8)展开等式左端，对等式积分可得

H=-Hmsin(ωt-βz)ax

(9)

可见磁场矢量H与电场矢量E同为正弦函数，且相位(ωt-βz)相同，仅矢量方向相差90°[22-23]，其与电场矢量运动的时空关系相同。

均匀平面电磁波的坡印廷矢量为

E×H=EmHmsin2(ωt-βz)az

(10)

其电磁场能量体密度为

(11)

对于电磁场上任一点相位为(ωt1-βz1)，经过Δt时间，该点到达z2点，Δz=z2-z1=vΔt，这时式(10)、(11)中正弦函数平方因子

sin2(ωt2-βz2)=sin2(ω(t1+Δt)-β(z1+Δz))=sin2(ωt1-βz1+(Δωt-βΔz))=sin2(ωt1-βz1)

(12)

可见不论是电磁波的功率流密度，还是电磁能量体密度，在电磁波运动中，都保持着正弦量平方的空间形态，以速度v直线前进[24-28]。这也再次体现了电磁波(场)的物质性。

2 圆极化电磁波

2.1 圆极化电磁波的形成

设有水平和垂直方向的两个线极化波Ex(z,t)，Ey(z,t)，它们振幅相等，Ey(z,t)相位超前Ex(z,t)90°，二者起始位置、计时时刻相同如式(13)所示。

(13)

它们的合成矢量为

E(z,t)=Ex(z,t)+Ey(z,t)=Em[sin(ωt-βz)ax+cos(ωt-βz)ay]

(14)

可见合成矢量E(z,t)与y轴夹角为

γ=ωt-βz

(15)

矢量幅度仍为Em.

当在某个确定的z0处垂直z轴的平面上，观察场量随时间的变化，矢量与y轴夹角

γ1=(ωt-βz0)

(16)

看到电场矢量幅度Em=常数，夹角随时间t以角速度ω旋转，矢量的矢端轨迹是一个圆，称为圆极化[29-31]。圆形成时有不同的旋向，当垂直线极化波Ey(z,t)导前水平极化波Ex(z,t)90°时，顺着波前进的方向看时，圆是逆时针旋转，称为左旋圆极化；当水平线极化波Ex(z,t)导前垂直线极化波相位90°时，圆是顺时针旋转的，称为右旋圆极化波[32-36]。

2.2 圆极化波电磁场量的时空关系

为了厘清概念，下面从分析圆极化波的空间分布着手，分析圆极化电磁场波的时空分布运动关系。

设在某个t=t0时刻，合成矢量为

E(z,t0)=Em[sin(ωt0-βz)ax+cos(ωt0-βz)ay]

(17)

矢量E(z,t0)与y轴夹角

γ2=(ωt0-βz)

(18)

仅是z值的函数，合成电场矢量E(z,t0)，是以系数(-β)随z值变化着与y轴夹角，形成一个以y轴为中心的空间的螺旋面分布[37-42]。E=(z,t0)的矢端轨迹是一个空间的螺旋线。

现在设以t=0，z=0为计算起始点，选择任意时刻t=t1，螺旋形上任一点z=z1，该处场矢量相应的空间夹角为

γ1=ωt1-βz1

(19)

电磁波以相速v运动后，同一点在t=t2时刻到达z=z2处，这时该点矢量的夹角为

γ2=ωt2-βz2

(20)

时间经过了t2-t1=Δt，电磁波沿z轴前进了z2-z1=Δz，代Δt，Δz关系入式(20)类似得到

γ2=ω(t1+Δt)-β(z1+Δz)=(ωt1-βz1)+(ωΔt-βΔz)=ωt1-βz1=γ1

(21)

(21)式说明，螺旋形上任意一点z处，电磁波运动的全过程中，任一场矢量的空间夹角γ=ωt-βz没有变化，螺旋形分布的电场矢量作着沿z轴直线平动的运动[43-45]。

2.3 圆极化电场矢量时空旋向的关系

以右旋螺旋空间分布的电场矢量为例，设t=t1,β>0，这时场矢量依z值由大处往z值小处看去，电场矢量与y轴夹角，γ=ωt1-βz按逆时针方向逐渐增加。因为z值大处的场矢量，较早通过某确定z0处的垂直平面，z值小处的场矢量较晚通过垂直平面，顺z轴正向看去，在以垂直平面上形成了逆时针旋转的圆形矢端轨迹，即左旋圆极化[46-48]。同样的道理右旋圆极化的空间矢端轨迹为左旋螺旋线[49-51]。磁场矢量时空旋向关系与电场相同。