一个数列问题的源与流

胡卫祖

(新疆博乐第五师高级中学 833400)

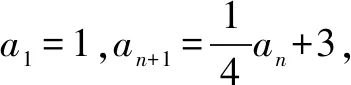
学生已有的基础是学习了等差、等比数列及其性质，对求数列通项主要会以下几类：根据等差、等比数列定义直接用公式求an；累加法求通项an；累积法求通项an；已知Sn根据an=Sn-Sn-1(n≥2)求an.但对上面提出来的问题用上面提到的方法都难奏效.如何能有效地求出an，使得教学自然合理，需要进行合理的教学设计.

一、回到基本概念中去寻找问题的答案

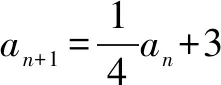
二、求实数k构造等比数列

三、总结提升，举一反三

推广：若已知数列{an}首项为a1，满足an=pan-1+q(n≥2),p,q∈R,p≠1，p,q为常数，求通项an

分析同上面的例题分析，我们希望构造出等比数列，即an=pan-1+q可化为an+k=p(an-1+k)，展开得an=pan-1+(p-1)k.

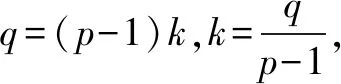
其基本原理是利用了待定系数法，构造出了等比数列.

四、巩固练习

练习题在于进一步理解问题，掌握该类型问题的转化与解答.课堂上应给予学生比较充分的时间练习，可以让学生上黑板板演.当然还可以多出几个练习题进行课堂练习.

五、延伸拓展

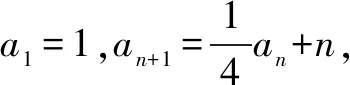
3.(高中数学人教A版必修5 P69第6题)已知数列{an}中a1=5,a2=2,an=2an-1+3an-2(n≥3)，对于这一数列的通项公式做一研究，能否写出它的通项公式？

分析同上面方法，我们尝试去构造等比数列，设an+α·an-1=β(an-1+α·an-2)，即an=(β-α)an-1+αβ·an-2，又an=2an-1+3an-2(n≥3)，故(β-α)=2,αβ=3，解得：α=1,β=3或α=-3,β=-1.

另解同上，取α=1,β=3，可得

an+an-1=7×3n-2①.

再取α=-3,β=-1,则有

an-3an-1=-(an-1-3an-2).

用上述方法可求得

an-3an-1=-13×(-1)n-2②.

将①与②联立，消去an-1,得

注：此题两次构造等比数列求通项an，但都是利用了等比数列的定义.

设计一个问题要善于回到基本概念中去，回到学生已有的知识体系中去，把看似高、大、上的问题化成很自然的学生能接受的知识.适当的归纳能够深化学生对知识的理解，适当的引申则是创新能力创新精神的体现.善于将知识的源与流进行合理设计，是教师上好课的努力的方向，也是教师价值的一种体现.