一类热工不稳定对象的抗重复扰动控制

马增辉，董 芳，徐慧仪



一类热工不稳定对象的抗重复扰动控制

马增辉1，董 芳2，徐慧仪1

（1.海南热带海洋学院海洋信息工程学院，海南 三亚 572022； 2.西安热工研究院有限公司，陕西 西安 710054）

本文针对不稳定的热工非自衡对象提出了一种控制方法，该方法对重复性扰动具有较突出的抑制能力。通过反馈补偿可以将含有积分环节的不稳定滞后过程IPDT模型补偿为二阶非最小相位对象。然后通过设计二阶系统的动力学通用控制器实现对IPDT模型的控制。同时，充分利用IPDT模型自身特性使系统对周期性重复扰动具有一定的抑制能力。仿真实验证明了该方法具有良好的控制特性和鲁棒性能。本文提出的方法结构简单，设计简便，容易在工程实践中推广应用。

热工控制；不稳定过程；非自衡对象；反馈补偿；通用控制器；重复扰动

非自衡对象是热工控制中一类较难控制的不稳定过程，如给水量扰动下的锅炉汽包水位控制，一直是学者研究的热点。文献[1]通过PD反馈补偿将非自衡对象转换为有平衡能力的等效对象，然后再使用预测函数的控制策略，该系统可以达到稳定状态，较快地跟踪设定值，但文献未对扰动的抑制能力进行讨论；文献[2]针对一类低增益非自衡对象，得到控制器参数整定经验公式，该经验公式仅提供了参数选取的大致范围，而且整定过程复杂，不利于工程推广应用；文献[3]设计了一种非自衡对象二自由度PID控制策略，其中低通滤波器参数决定了系统性能，且未给出确定的滤波器参数整定公式；文献[4]针对一类非自衡对象，在内模控制原理的基础上，导出一种基于典型反馈模型的PID参数整定策略，从仿真结果看，未达到最佳的抑制扰动效果，超调量过大，且系统整定参数较多。

工程中控制对象往往受到某一类扰动的频繁干扰，在一段时间周期内，可以将这类扰动视作重复性的干扰信号。在控制策略中，希望系统能够快速、无差地跟踪任意周期的扰动信号。也就是说，系统克服重复性扰动的能力至关重要。文献[5]将未知扰动视为仅沿时间轴变化的扰动与随时间轴和迭代轴均变化的扰动的叠加，针对一类单输入单输出高阶非线性系统，设计了滑模鲁棒迭代学习算法；文献[6]将改进型分数阶PID控制与重复控制结合，利用重复控制与周期性输入或复杂干扰信号的跟踪和抑制能力来提高系统的快速响应能力和抗干扰性；文献[7]针对一类周期参考信号下不确定离散系统的跟踪控制问题，将误差动态补偿方法用于构造理想误差动态方程以设计重复控制器；文献[8]在系统前端通过重复控制对误差信号进行周期性补偿，在系统后端设计了基于扰动频率自适应的扩张状态观测器，提出了一种基于重复控制和自抗扰理论的控制器设计方案；文献[9]提出了一种基于重复自抗扰控制的感应电机矢量控制方法，通过融入重复控制，提升了传统感应电机自抗扰控制系统抗扰动的能力；文献[10]设计非线性扰动观测器用于估计外界干扰，并在非线性最优控制律中进行干扰补偿；文献[11]针对具有执行器故障和外界扰动的线性重复过程，给出一种鲁棒迭代学习容错控制策略；文献[12]在趋近律中嵌入扰动抑制措施，设计重复控制器抑制周期性扰动。

本文通过反馈补偿将不稳定的非自衡过程，补偿为二阶非最小相位对象，通过设计二阶系统的动力学通用控制器来实现非自衡过程的控制，同时利用时滞学习环节提高系统抑制周期性扰动的能力。

1 动力学通用控制器

文献[13]根据稳定时不变二阶对象提出了一种基于动力学通用控制器，即

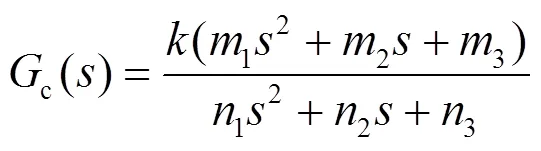
式(1)表示通过系统的运动位置3、速度2和加速度12的负反馈作用使系统达到预期的控制效果。加速度12的负反馈作用非常重要，它能够提高系统的控制品质和鲁棒性。

PID控制器的传递函数为

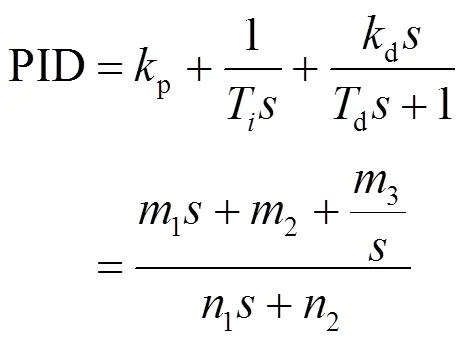
式(2)是当=1、3=0时通用控制器式(1)的一个特例，它没有加速度控制作用。

对于不稳定对象，可以先设计动态补偿器使之稳定，然后再进行通用控制器设计。将系统的输出与期望的闭环系统的输出相比较容易得到式(1)中、1、2、3、1、2、3的值。

2 非自衡对象分析

含有积分环节的不稳定滞后对象IPDT模型为

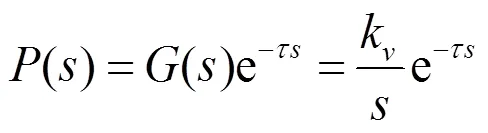
由于()含有一个=0的极点，若要系统闭环稳定，则需要设计补偿器，最简单的办法是配置一个零点=0，用以抵消IPDT模型中不稳定的极点。

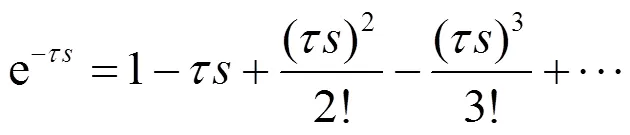
在反馈回路设计补偿器[14]如图1所示。

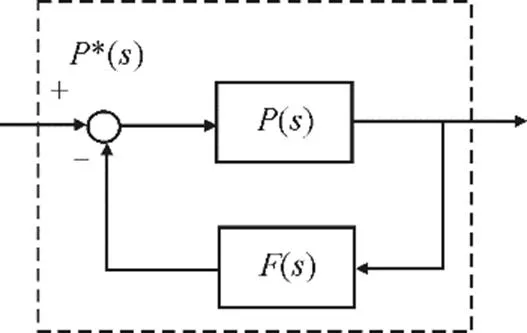
图1 反馈补偿对象

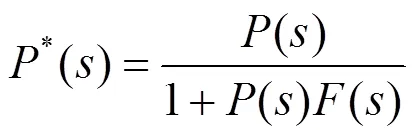
将式(3)、式(5)代入式(6)得

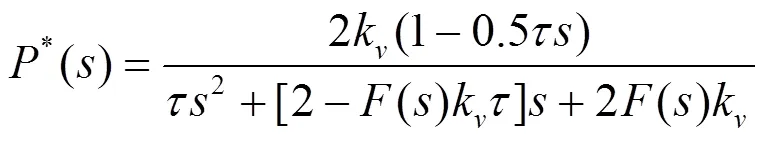
由式(7)可以看出，只要设计补偿器()为一个比例环节即可将原来的不稳定系统转变为一个二阶非最小相位对象，而对于含有右半复平面零点的非最小相位系统的控制可以通过设计二阶系统的通用控制器来实现。

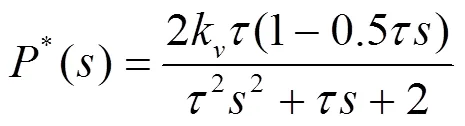
3 非自衡对象控制方案

3.1 二阶控制器整定

由以上分析可知，非自衡对象的控制可以转化为非最小相位对象的二阶控制器设计问题，控制方案如图2所示。

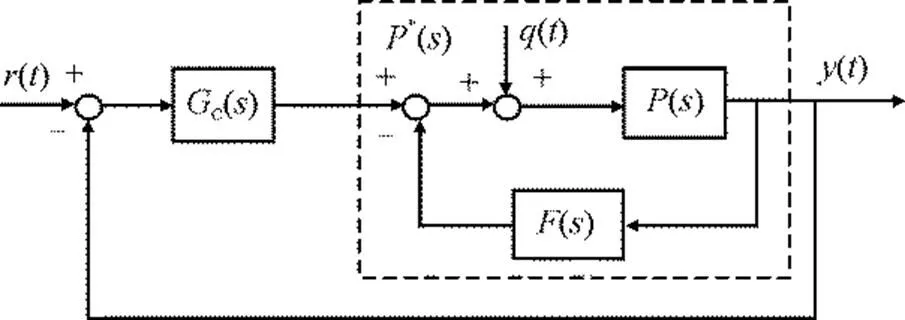
图2 非自衡对象控制方案

二阶通用控制器设计步骤如下：

2）式(1)中，3=0，系统无差；

3）2=1.5，1=2，=1, 2, 3…，考虑到系统稳定性，建议取稍大值，通常选取=8~10；

4）1=2，2=1.5，3=1；

5）通用控制器比例系数和可通过选取不同的目标函数求得，如选取ITAE指标(integrated time absolute error criterion)即可。

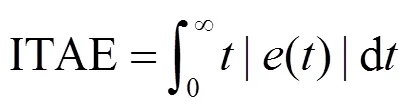
3.2 扰动抑制分析

内部模型定理[15-16]：假设图2所示的闭环系统是稳定的，则控制对象的输出()无稳态偏差地跟踪参考输入()的充要条件是环路传递函数()=c()*()包含有参考输入()的产生模型R()=-1[()]。

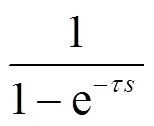
图2中扰动量()经过()反馈到控制器c()的输入端。相当于扰动量()经积分环节1/反馈到控制器的输入端。扰动()充分利用了对象时滞环节的记忆特性，利用1个周期以前的信息()不断学习积累从而获得高精度的跟踪性能；对象的积分环节1/恰恰也提高了在扰动激励作用下的系统控制品质。所以该方法对一定周期的重复性扰动具有良好的抑制作用。特别是，满足≤，是重复性扰动信号的周期，对扰动的跟踪能力最强，该系统对扰动的抑制能力也最明显。

4 仿真实例

4.1 仿真结果

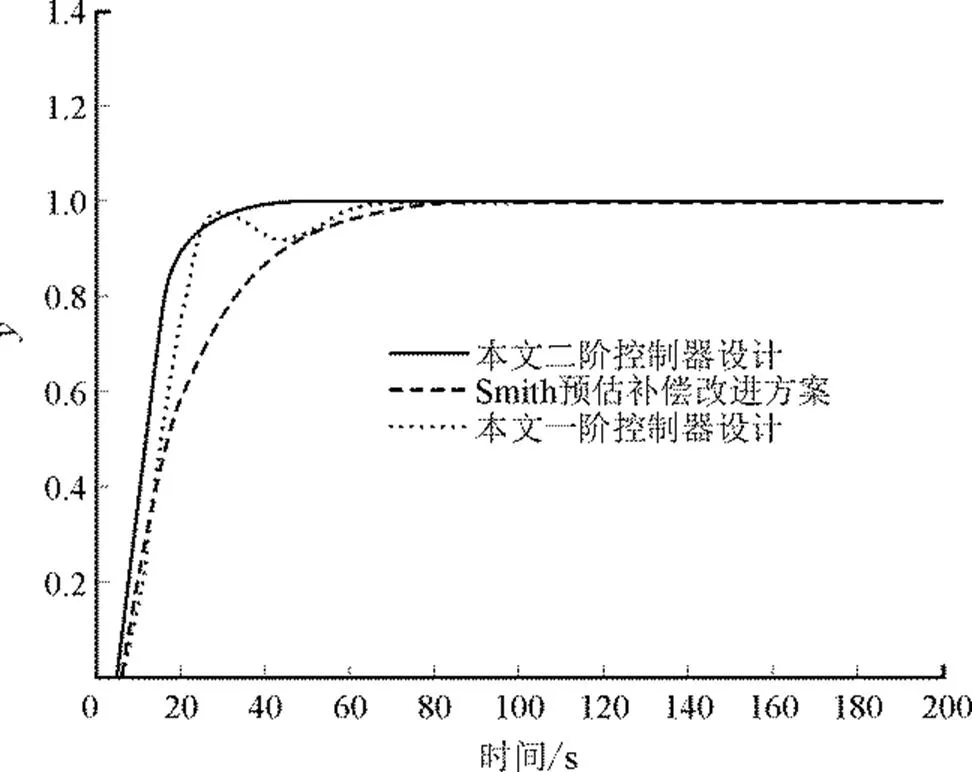
图3 3种控制器仿真结果对比

4.2 鲁棒性检验

控制器参数保持不变，对象()的参数k和滞后时间分别增大和减小10%和20%，系统的仿真结果如图4所示，当对象参数k和增大20%时，系统出现了一定的波动，可以通过调整二阶控制器前置系数来解决。对模型不确定性而言，系统的鲁棒性较好。

4.3 周期性扰动测试

在端分别加入幅值20%的正弦和锯齿波扰动，正弦扰动见表1，仿真结果如图5所示。

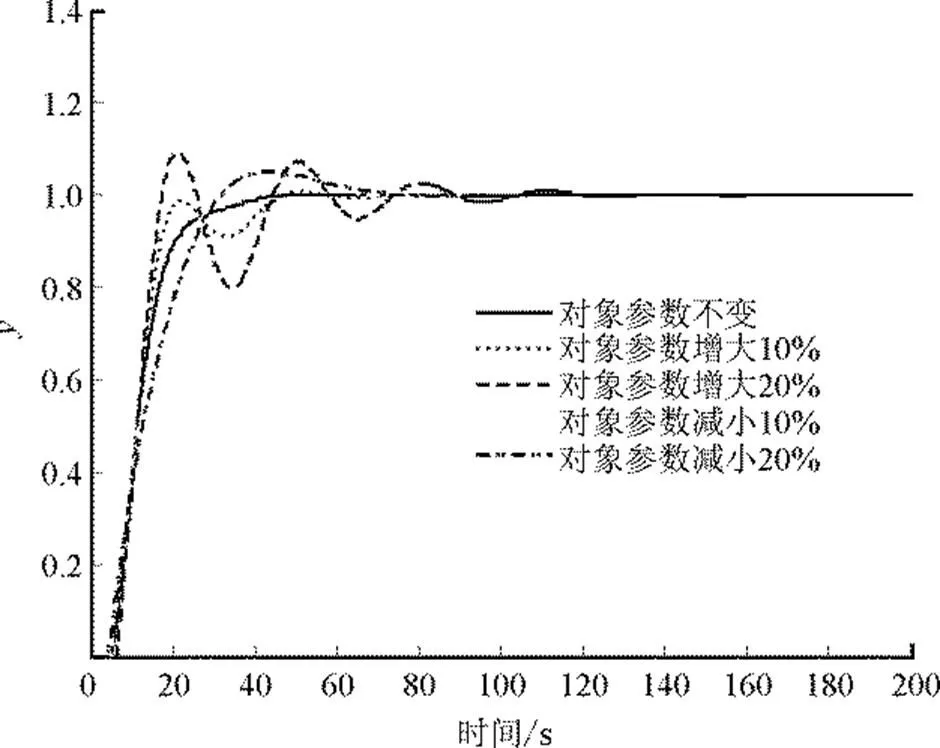
图4 鲁棒性检验

表1 正弦扰动参数

Tab.1 The sinusoidal disturbance parameters

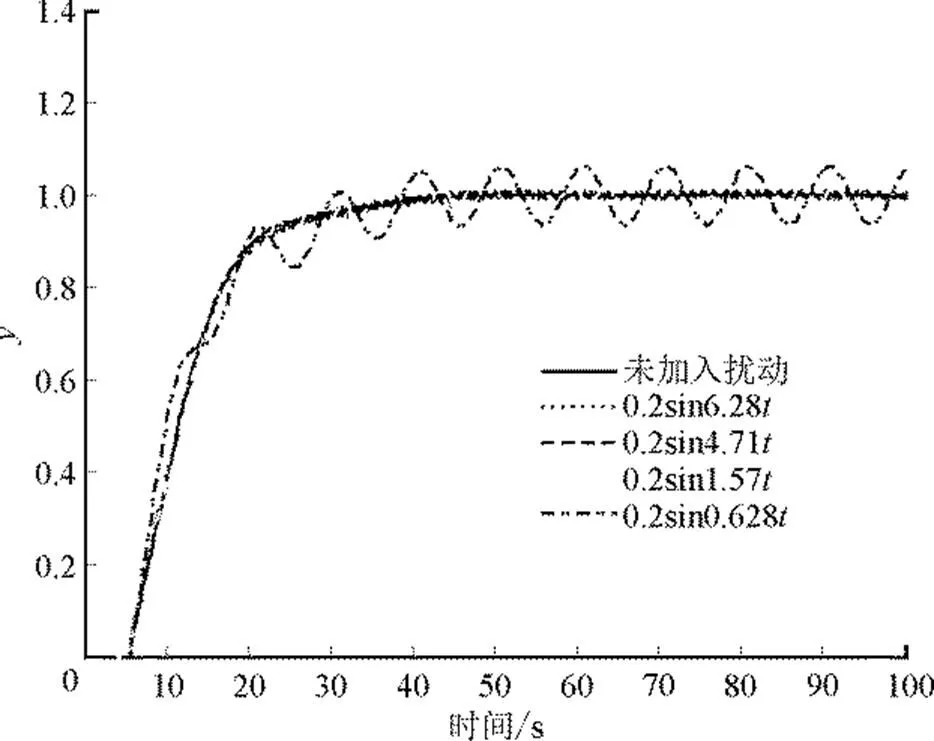
图5 正弦扰动仿真结果

在扰动端加入幅值20%，周期分别为2、5、10、15 s的锯齿波，仿真结果如图6所示。

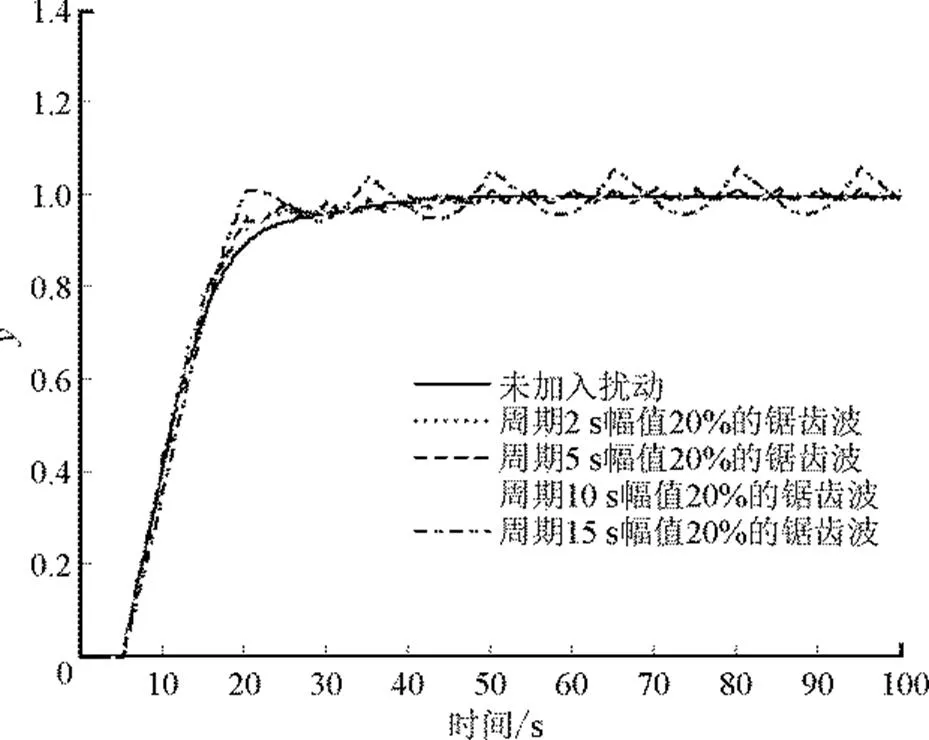
图6 锯齿波扰动仿真结果

由图5和图6可以看出，当扰动周期≥2时，系统对周期性扰动的抑制能力逐渐变弱。

5 结 论

1）通过反馈补偿可以将含有积分环节的不稳定滞后过程（IPDT模型）补偿为二阶非最小相位对象。对于含有右半复平面零点的非最小相位系统的控制可以通过设计二阶系统的通用控制器来实现。仿真结果表明，二阶控制器由于含有系统运动的加速度项，控制效果要优于一阶控制器；同时，本文提出的方法设计简便，控制效果优于Smith预估补偿的方法，而且具有较好的鲁棒性能。

2）扰动量充分利用对象滞后环节的记忆特性，经积分环节反馈至控制器的输入端，能够快速、无差地跟踪任意周期的扰动信号。仿真结果证明该方案对周期性的重复扰动具有一定的抑制能力。

［1］ 何同祥, 房芳. 一类非自衡对象的预测函数控制[J]. 仪器仪表用户, 2016, 23(3): 46-48.

HE Tongxiang, FANG Fang. Predictive functional control in a kind of no self-regulating process[J]. Instrumentation, 2016, 23(3): 46-48.

［2］许向阳, 刘业彬, 杨忠琳, 等. 针对非自衡对象的蝎子控制算法研究[J]. 化工自动化及仪表, 2016, 12(2): 1281-1285.

XU Xiangyang, LIU Yebin, YANG Zhonglin, et al. Research of the scorpion algorithm for an integrator process[J]. Control and Instruments in Chemical Industry, 2016, 12(2): 1281-1285.

［3］温馨, 石红瑞. 积分过程的二自由度PID控制及应用[J]. 控制工程, 2013, 25(增刊1): 206-217.

WEN Xin, SHI Hongrui. Two degree of freedom PID control for integral processes and its application[J]. Control Engineering of China, 2013, 25(Suppl.1): 206-217.

［4］冀晓翔, 汤伟. 一类非自衡对象的典型反馈型PID控制[J]. 计算机测量与控制, 2012, 20(5): 1265-1275.

JI Xiaoxiang, TANG Wei. Typical feedback PID control for a class of process with integrator and dead time[J]. Computer Measurement & Control, 2012, 20(5): 1265-1275.

［5］吕庆, 方勇纯, 任逍. 含非严格重复扰动的抗扰迭代学习控制[J]. 控制理论与应用, 2014, 31(9): 1190-1197.

LYU Qing, FANG Yongchun, REN Xiao. Anti-disturbance iterative learning control for nonlinear systems with time-iteration-varying disturbances[J]. Control Theory & Applications, 2014, 31(9): 1190-1197.

［6］刘春芳, 刘志. 基于分数阶PID和重复控制的快速刀具伺服系统[J]. 沈阳工业大学学报, 2017, 39(5): 486-490.

LIU Chunfang, LIU Zhi. Fast tool servo system based on fractional order PID and repetitive control[J]. Journal of Shenyang University of Technology, 2017, 39(5): 486-490.

［7］周文委, 孙明轩, 张有兵. 带扰动补偿的无抖振离散重复控制器设计[J]. 控制与决策, 2017, 32(3): 467-473.

ZHOU Wenwei, SUN Mingxuan, ZHANG Youbing. Chatting-free discrete-time repetitive controller design with disturbance compensator[J]. Control and Decision, 2017, 32(3): 467-473.

［8］魏伟, 戴明, 李嘉全, 等. 基于重复-自抗扰控制的航空光电稳定平台控制系统设计[J]. 吉林大学学报(工学版), 2015, 45(6): 1924-1931.

WEI Wei, DAI Ming, LI Jiaquan, et al. Design of airborne opto-electric platform control system based on ADRC and repetitive control theory[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(6): 1924-1931.

［9］杜超, 尹忠刚, 李艳琴, 等. 基于重复自抗扰控制的感应电机矢量控制方法[J]. 电工技术学报, 2017, 32(19): 81-89.

DU Chao, YIN Zhonggang, LI Yanqin, et al. Research on repetitive-auto disturbance rejection control strategy for induction motors based on vector control[J]. Transations of China Electrotechnical Society, 2017, 32(19): 81-89.

［10］ 余光学, 李惠峰. RLV抗扰动非线性最优控制器设计[J]. 控制与决策, 2015, 30(3): 513-518.

YU Guangxue, LI Huifeng. Anti-disturbance nonlinear optimal controller design for RLV[J]. Control and Decision, 2015, 30(3): 513-518.

［11］ 陶洪峰, 邹伟, 杨慧中. 执行器故障重复过程的鲁棒迭代学习容错控制方法及应用[J]. 控制与决策, 2016, 31(5): 823-828.

TAO Hongfeng, ZOU Wei, YANG Huizhong. Robust iterative learning fault-tolerant control method and application for repetitive process with actuator fault[J]. Control and Decision, 2016, 31(5): 823-828.

［12］ 孙明轩, 王辉, 范伟云. 以幂次趋近的离散变结构重复控制[J]. 控制理论与应用, 2012, 29(11): 1426-1432.

SUN Mingxuan, WANG Hui, FAN Weiyun. Discrete-time variable-structure repetitive control with power-rate reaching[J]. Control Theory & Applications, 2012, 29(11): 1426-1432.

［13］ 刘建民, 韩璞, 开平安, 等. 基于动力学等价的一种通用控制器设计[J]. 控制理论与应用, 2008, 25(6): 1155-1157.

LIU Jianmin, HAN Pu, KAI Ping’an, et al. Design of a general controller based on dynamics identity[J]. Control Theory & Applications, 2008, 25(6): 1155-1157.

［14］ NORMEY-RICO J E, CAMACHO E F. Control of dead-time processes[M]. London: Springer-Verlag, 2007: 256-258.

［15］ 钟庆昌. 时滞控制及其应用研究[D]. 上海: 上海交通大学, 1999: 103-104.

ZHONG Qingchang. Time delay control and its applications[D]. Shanghai: Shanghai Jiao Tong University, 1999: 103-104.

［16］ BENGTSSON G. Output regulation and internal model: a frequency approach[J]. Automatica, 1975, 13: 333-345.

Repetitive disturbances rejection control for a class of thermal unstable process

MA Zenghui1, DONG Fang2, XU Huiyi1

(1. College of Marine Information Engineering, Hainan Tropical Ocean University, Sanya 572022, China; 2. Xi’an Thermal Power Research Institute Co., Ltd., Xi’an 710054, China)

A control method for unstable thermal non-self-balancing objects is proposed, which has remarkable ability to restrain repetitive disturbances. In this method, the IPDT model of unstable hysteresis process with integral link can be equivalent to a two-order non-minimum phase system through feedback compensation. Then, by designing a dynamics general controller, the IPDT model can be controlled. At the same time, by making full use of the self-characteristics of the IPDT model, the system has a certain ability to inhibit the periodic repetitive disturbances. Simulation test results show this method has good control performance and robustness, it is simple in structure and design, and easy to be popularized and applied in engineering practice.

thermal engineering control, unstable process, non-self-balancing object, feedback compensation, general controller, repetitive disturbance

TP273; TK323

A

10.19666/j.rlfd.201809116

马增辉, 董芳, 徐慧仪. 一类热工不稳定对象的抗重复扰动控制[J]. 热力发电, 2019, 48(5): 145-149. MA Zenghui, DONG Fang, XU Huiyi. Repetitive disturbances rejection control for a class of thermal unstable process[J]. Thermal Power Generation, 2019, 48(5): 145-149.

2018-09-18

海南省自然科学基金资助(619MS070)

Natural Science Foundation of Hainan Province (619MS070)

马增辉(1977—)，男，博士，高级工程师，主要研究方向为火电厂热工自动控制、节能优化理论等，mzh_1220@126.com。

（责任编辑 杜亚勤）