深空机动对运载火箭发射火星探测轨道研究

2019-06-05耿光有张志国王建明田继超

宇航学报 2019年5期

耿光有，王珏，张志国，王建明，田继超

(1.北京航空航天大学宇航学院，北京 100191；2.北京宇航系统工程研究所，北京 100076；3.中国运载火箭技术研究院，北京 100076)

0 引言

运载火箭发射火星探测器等深空任务时，通常需要先进入低高度地球停泊轨道，待火箭滑行至预定位置后再次点火，从而将探测器送入奔赴火星的转移轨道，新一代低温长征火箭从海南发射火星探测器时，除了受到航落区安全及地面测控等因素的限制外，还有低温入轨级两次起动间最长允许滑行时间的严格限制[1-2]，使入轨点位置(或近地点幅角)的调节范围较为有限，为满足2～3周的有效发射日期窗口[3]，通常解决方法是加大射向(对应出发轨道倾角)或增加出发点速度能量，但加大射向会受到航落区限制，增加出发点速度能量一般也将增加探测器抵达火星时需要的制动速度增量，因此工程实现效果并不十分理想；而成功解决上述问题获得更多优质发射机会，是促成火星等深空探测工程顺利实施的重要衡量指标；如果能在探测器从地球至火星耗时数月的转移轨道途中，通过施加一合适的速度增量以解决上述问题，工程意义将是重大的；本文研究化学推进的火星探测器深空机动指可以等效为速度脉冲增量的中途机动。Fimple[4]曾提出在深空轨道与黄道面的升(或降)交点处，增加一次轨道面机动可以减小总速度增量，耿长福[5]、戴光明[6]介绍并推广了这一思想，但考虑多天体摄动等影响因素后，最优深空机动点位置可能已偏离轨道升(或降)交点很远，而由于机动点具体位置和时刻一般相互独立，因此很难用简单的一维搜索予以解决；注意到深空机动的位置完全可能大幅度变化，因此在获得一个良好的猜测初值前，综合机动点位置与时刻四维搜索需要的计算量一般难以被接受。Lawden[7]提出主矢量法用于转移轨道机动分析，Lion等[8]据此分析了非最优轨道，文献[9-10]推广了应用，Conway[11]指出当不满足Lawden必要条件时，通过增加深空机动是有用的，Iorfida等[12]采用极坐标开展了轨道面内、外中途修正(或深空机动)的进一步研究；Glandorf[13]将主矢量法拓展到圆锥曲线[14]轨道拼接，Navagh[15]、Olympio等[16]采用主矢量法分析了多天体借力飞行时深空机动的优化问题，Olympio等给出了利用深空机动减小行星借力飞行中总速度增量的算例，并指出地球到火星借力飞行中一般仅需要一次深空机动，只有与黄道面近乎垂直的转移轨道需要两次深空机动，基本不需要两次以上深空机动；乔栋等[17]采用主矢量法分析了深空多脉冲机动下的发射机会搜索，沈红新[18]对脉冲推力最优轨迹的Hamilton边值统一性问题进行了分析，潘迅等[19]将主矢量法应用于月地平动点双脉冲转移轨道的寻优快速确认中；但上述文献均没有行星引力影响球内飞行段的详细分析研究，而对于长征运载火箭发射火星探测任务来讲，深空机动能否降低运载火箭出发与探测器抵达火星的总速度增量，能否通过深空机动解决受运载火箭最长允许滑行时间与航落区限制下的发射日期窗口拓展等工程设计问题，亟需深入开展研究。

综上，结合工程实际，本文采用主矢量法结合序列二次规划[20]寻优算法，完成了包括运载火箭地面发射起飞至探测器抵达近火点目标轨道，通过火星探测器转移轨道深空中途增加一次速度脉冲机动(以下称深空机动)下的系统优化研究。

1 分析模型及算法

当确定了运载火箭的发射日期与探测器抵达火星日期，一般即可以开展无深空机动下，运载火箭发射火星探测转移轨道的优化分析计算。

1.1 火星探测发射轨道设计基本力学模型

采用火星探测器近火点目标轨道参数，由运载火箭完成抵达近火点的直接转移轨道详细设计分析可参见本人新近另外著述等，限于篇幅，此处仅给出扼要介绍。

在起飞时刻地心惯性系下，运载火箭穿越大气飞行段的质心动力学矢量方程[21-22]为：

(1)

(2)

从探测器分离开始，整个地火转移轨道都在日心J2000坐标系下完成积分，动力学方程如下：

(3)

采用双向微分修正算法进行计算，其思路见文献[23]，此算法与文献[25]的直接打靶法有相通之处，优点是便于增加深空速度脉冲后的深入优化。

(4)

在近地出发点，存在3个约束：

(5)

在火星进入段，双曲线轨道的三个约束：

(6)

正反双向积分的相遇历元时刻为Tm时：

(7)

式中:上标“+”表示正向积分轨道，上标“-”表示反向积分轨道，分析表明，连接点可以较大自由度选择，初值不妨取Tm=(T1+T2)/2，即中间历元时刻。

在方程(5)～(7)中给出了12项约束，采用牛顿迭代求解雅可比矩阵就可以完成运载火箭火星探测发射轨道分析设计。

1.2 主矢量算法猜测深空机动最优初值

1.2.1主矢量理论及特性

Bryson和Ho[26]给出了动力学方程(8)下的哈密顿方程(9)：

(8)

式中：X为状态量，rt为t时刻位置矢量，Vt为t时刻速度矢量，g(rt)为引力加速度，Γ为脉冲推力加速度，u(t)为推力的单位方向矢量。

(9)

式中：λr，λv为协态变量。

对于脉冲推力情况，增加一次深空机动后，成本函数为沿转移轨道脉冲速度增量累计和[10-11]：

(10)

根据极小值原理，方程(9)的伴随方程为：

(11)

λ(t)≜-λv(t)

(12)

(13)

综合式(11)～(13)，有：

(14)

对于最优转移轨道，主矢量满足以下四个必要条件[7,10]：

(1)主矢量与它的微分处处连续；

(2)转移期间主矢量模不超过1；

(3)如果存在中间推力脉冲时刻，主矢量方向与推力一致，其模为1；

(4)所有中间推力脉冲时刻的主矢量导数为0。

通过沿转移轨道积分获取λ(t)曲线，可以快速判断转移轨道是否最优，按照条件(1)～(2)判定是否需要增加中途机动完成发射转移轨道进一步优化，对符合条件的采用主矢量法可快速完成最优机动初值猜测，因此主矢量法已逐渐演化成一种重要的轨道中途机动优化方法。

根据主矢量必要条件可以给出主矢量边界条件[11]，定义主矢量初值及终态分别见式(15)、(16)：

(15)

(16)

式中:下标0表示起始状态，f表示终端状态，下同。

由方程(14)可得：

(17)

由式(17)可知，

(18)

1.2.2分析参考轨道主矢量曲线及转移矩阵

依据主矢量特性，采用式(19)～(21)沿参考轨道得状态转移矩阵φ(t,t0)。

φ(t0,t0)=I

(19)

(20)

(21)

根据主矢量定义，结合式(15)～(18)，采用式(22)得λ(t)曲线。

(22)

1.2.3增加一次脉冲机动后最优初值猜测

对于两脉冲转移轨道，成本函数为：

(23)

采用Jezewski[10]的思路，当增加一次中途脉冲机动后，成本函数变为：

(24)

式中:右上角“+”表示脉冲机动后，“-”表示脉冲机动前，下同。

dJ=J1-J0

(25)

结合伴随方程式(26)：

(26)

当起止端位置固定，在一阶摄动下，可得式(27)：

(27)

将式(25)采用幂级数展开至二阶项，再结合式(26)，写成c的二次方程，并取∂(dJ)/∂c=0，得摄动速度c：

(28)

(29)

(30)

(31)

此时，脉冲机动后最优轨道所需位置rdsm与原指定参考轨道位置rnom和摄动量∂rm见式(32)～(33)：

rdsm=rnom(tm)+∂rm

(32)

(33)

对于工程中感兴趣的地火直接转移轨道，一般可以通过式(28)～(33)获得深空机动最优猜测初值。

1.2.4多中心天体引力下状态转移矩阵

由于工程中需要考虑地球或火星引力影响球内飞行段，经推导分析，对地球至火星转移轨道，采用主矢量算法需要补充以下内容。

引力梯度矩阵式(21)需要修正为式(34)，式中ri为运载火箭或探测器相对地球(i=E)或火星(i=M)的位置矢量：

(34)

数值计算情况下，穿越影响球边界时的6×6阶状态转移矩阵：

(35)

式(35)对引力影响球边界具体尺度不是特别敏感，以地球为例，设置距地心1000000 km处，注意到此式引起的主矢量一阶导数不连续是由于引力中心坐标转换引起，因此与Lawden主矢量特性必要条件并不抵触；但新情况下需要深入具体分析。

当飞出地球影响球时，设t=t1，此时：

(36)

当飞入火星影响球时，设t=t2，此时：

(37)

其中,

(38)

式(36)～(38)中：P*,Q*分别指探测器在地球(或火星)引力边界处相对日心的位置及速度；式(38)中“+”表示离开影响球，“-”表示进入影响球；式中右上角标“+”表示过影响球边界后，“-”表示之前。

这样，从地球停泊轨道出发到进入环火星目标轨道，涉及到的总过渡转移矩阵为：

ψ(tf,t0)=φ(tf,t2)w(t2)φ(t2,t1)w(t1)φ(t1,t0)

(39)

与式(39)相匹配时，式(24)代表的累计速度指相对于地球停泊轨道出发速度增量、抵达火星目标轨道速度增量和中途深空机动脉冲速度增量。基于当前文献中多以忽略引力影响球内飞行段，即以引力影响球边界处速度增量为关注点，为便于对比，需将式(24)变为式(40)：

(40)

式中:下标E0指相对于地球中心，下标Mf指相对于火星中心。

1.2.5起始、抵达时刻与深空机动时刻的调整优化

对于满足主矢量必要条件，但总速度增量仍明显高于所在年份最低速度增量[27]的转移轨道，说明增加深空机动难以进一步降低成本函数，此时需要进一步优化起始与抵达时刻，分析如下。

对于包含一次深空脉冲机动下，t时刻状态量的Lambert求解问题：

(41)

在数值寻优状态下，成本摄动函数表示为：

(42)

式中:下标m表示脉冲机动状态，下同。

对于从初始轨道转移至目标轨道的一般问题，根据式(9)哈密顿函数，结合主矢量定义及伴随方程式(26)，在滑行段，有：

(43)

沿着Jezewski[10]的思路，对于地球到火星转移轨道，速度脉冲作用下，得成本摄动函数式：

(44)

1.2.6采用主矢量猜测最优初值算法步骤

采用主矢量算法获得深空机动最优猜测初值的算法步骤见图1，图中关于“需调整出发抵达日期”主要指式(44)描述的转移轨道情况。

图1 采用主矢量算法获得深空机动最优猜测Fig.1 Obtaining initial guess of DSM via primer vector

1.3 序列二次规划数值寻优算法

利用深空机动最优猜测初值，进一步采用序列二次规划(SQP)寻优算法[6,20]完成数值优化；其非线性规划的描述为：

(45)

基于关注的工程目标关系，式中t1，t2分别表示地球与火星引力影响球边界跨越时刻。

约束条件为：

(46)

式中:ΔVmB表示允许的深空机动最大速度值。当限定运载火箭在停泊轨道的最长滑行时间时，需增加：

Th≤ThB

(47)

式中:ThB表示为限定运载火箭在停泊轨道的最长滑行时间。

由于机动点速度与机动时刻相互独立，故取优化变量为：

(48)

因为不同机动时刻所需要的ΔVm变化幅度较大，所以tm变化后，轨道基准点需要根据上一时刻地火转移轨道获得：

(49)

式中:上标“′”表示轨道新时刻基准点。

2 仿真分析与算例

本文分析算例中，初始轨道以长征火箭从海南发射场起飞，设定一初始射向A0(对应相应轨道倾角)，停泊轨道暂设为高度200 km圆，探测器分离时真近点角约25°；探测器抵达近火点的目标轨道高度为500 km圆，近火轨道倾角93°，到达近火点成为圆轨道时优化结束。

2.1 地球或火星逃逸速度与近地点或近火点速度

根据近地点或近火点与引力影响球半径处速度关系：

(50)

式中：下标p表示近地点或近火点，∞表示引力影响球半径处。

相对近行星点时刻圆轨道的速度增量为：

(51)

由式(51)可知，近地点(或近火点)速度增量与地球(或火星)引力边界逃逸速度不是简单的线性关系，故采用不同优化目标J2或J1得到的结果将存在一定差异。

2.2 地球到火星探测轨道深空机动分析算例

以2020年7月23日出发，约340天转移，2021年6月28日中午抵达近火点目标轨道的计算为例，主矢量曲线图如下。

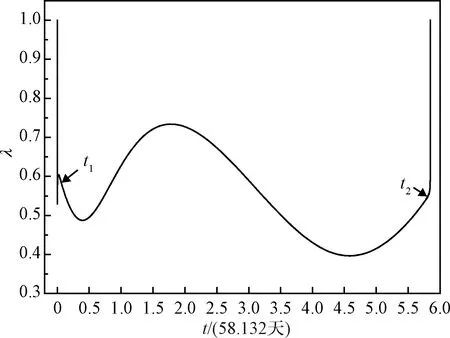
图2 参考轨道的λ～t曲线Fig.2 History of primer vector on reference trajectory

从图2可以看出，算例中从地球出发到抵达近火点轨道转移过程中的主矢量峰值小于1，但结合主矢量定义及穿越引力影响球对主矢量参数曲线计算的影响，再从地球引力影响球边界到火星引力影响球边界的过程来看，很可能存在通过深空机动进一步降低成本函数的可行性，具体需要采用数值寻优算法进一步分析确认。

图曲线Fig.3 Primer history of on reference trajectory

从图3结合式(44)来看，调整出发与抵达日期均可以使转移轨道发射总能量进一步降低，尤其是调整出发日期可以更明显降低转移轨道发射总能量,篇幅所限,此分析从略;下面重点关注深空机动后的效果影响,在主矢量法最优猜测初值基础上，依据不同优化目标及约束，采用SQP算法数值寻优结果，具体优化结果见表1。

表1中，J1=ΔVEp+ΔVm+ΔVMp，指相对地球及火星停泊轨道速度增量与深空机动速度三者累计和；J2=ΔVE0+ΔVm+ΔVM0，指地球及火星引力影响球边界速度增量与深空机动速度三者累计和；表头中“J1目标Th≤400 s”指采用J1目标进行优化且限定运载火箭停泊轨道滑行时间限定为不超过400 s；表中计算约束除采用射向A0=107°，对应出发轨道倾角25.5°外，其它如近地点高度等均同前述。

从表1可以看出，在设定的近地点与近火点轨道约束，以及限制运载火箭停泊轨道最长滑行时间条件下：

1)最优猜测初值给出的优化时机在出发后第101.9天，具体设计轨道约束下，采用SQP算法数值寻优结果为141.8天到149.8天，即采用主矢量法获得了良好初值。

表1 采用SQP算法数值寻优结果Table 1 The numerical optimal results using SQP

2)采用J2为优化目标，可将初始轨道的J2=7562.8 m/s降低到J2=6758.0 m/s，降低了804.8 m/s，虽然J1仅降低了8.6 m/s，但总的优化效果巨大。

3)采用J1为优化目标，可将初始轨道的J1=6377.1 m/s降低到J1=6347.7 m/s，降低了29.4 m/s，J2也降低了514.4 m/s，故优化效果明显。

4)采用J1为优化目标且同时限定火箭停泊轨道最长滑行时间不超过400 s，则可以优化到J1=6367.5 m/s，相比初始轨道可以降低9.6 m/s，相比不约束状态多消耗了19.8 m/s，即通过深空机动完全可以调整运载火箭发射探测器入轨点的位置，而且消耗的总发射能量在可接受范围内，故通过深空机动有效拓展发射日期窗口的优化效果明显。

注意到上述优化求解是在严格限定近地点与近火点高度、倾角与真近点角约束下获得的，而大多数行星际借力飞行等任务，只需要近星点最低高度约束，因此一般更易获得进一步优化的结果。

此外，研究分析发现：对地球到火星转移轨道，只要主矢量曲线形状能如图2所示，即从地球引力影响球边界t1到火星影响球边界t2间，主矢量曲线中有高于t1或t2处的峰值，则如果以J2为优化目标，一般均能找到更优目标；而同等情况若以J1为优化目标，除非总速度增量已接近(调整出发与抵达日期后得到的)最优解[27]外，则一般也总能通过深空机动找到更优解(如算例所示)。通过上述分析表明：深空机动对于降低运载火箭出发与探测器抵达火星的总速度增量，解决运载火箭受最长滑行时间与航落区限制下的发射日期窗口拓展等问题，意义显著，虽然考虑引力影响球内飞行过程的优化求解是非常复杂的。由于进一步的具体分析是非常复杂的工程问题，限于篇幅等因素，这里不再赘述。

综上分析，可以得出结论：

1)利用主矢量法判断并获取猜测初值、再进一步由序列二次规划算法完成精确数值寻优，可以很好地实现多中心天体引力下的轨道优化。

2)采用J1、J2或J1且限定运载火箭停泊轨道最长滑行时间等不同优化目标，所得到的最终优化点存在差异，故具体优化目标需要视工程情况而确定。

3)采用深空机动可以降低总速度增量，但要想大幅度降低近地点出发与抵达近火点的速度增量是困难的，原因与卫星轨道近地点加速时更易提高飞行轨道能量本质原理一致。

4)采用深空机动，通过深空中途小幅速度机动，可以调整对运载火箭入轨点位置的需求，即深空机动可以扩展发射日期窗口机会。