不同加载速率下砂岩弯曲破坏的细观机理*
2019-06-05李柯萱
李柯萱,李 铁
(1.北京科技大学金属矿山高效开采与安全教育部重点实验室,北京 100083;2.北京科技大学土木与资源工程学院,北京 100083)
岩石是由一种或几种矿物或玻璃按照一定的方式组成的集合体,因而岩石具备各种孔隙、孔洞、裂隙及各种成岩缝。在荷载作用下岩石会出现宏观破坏,这与其内部微裂纹和孔隙等缺陷的分布以及微裂纹的产生发育、扩展、聚集和贯通密切相关[1]。因此,岩石断裂是外部力学加载及内部结构共同决定的,岩石断口表面形貌通常能揭示其变形破坏的本质,是联系岩石断裂宏观力学行为和微观破裂机制间的桥梁[2]。近年来,学者们对岩石断口细观形貌进行了研究,取得了一定的成果和进展[3-5]。但多数集中在对岩爆、动态荷载作用下断口的细观形貌和力学行为之间联系的研究[6-8]。如李德建等[1]对岩爆碎屑表面电镜扫描图片进行裂纹分析,计算细观裂纹分形维数,表明岩爆裂纹的分形维数与岩爆发生过程的应力转化过程密切相关。朱珍德等[9]对大理岩破断面进行电镜扫描,得出莫尔强度包络线在低围压作用下几乎为线性,在高围压作用下则呈非线性;探讨了高围压高水压作用下破裂的微观损伤特性和微观损伤力学机理。Li等[10]对动荷载作用下岩石破裂过程中的能量特征进行了定量分析,得出了细观形貌特征受能量影响的结论,因此岩石破裂过程中吸收的能量越多,岩石碎裂程度越高。赵康等[11]对岩爆岩石的断口进行了扫描电镜细观分析,发现巷道围岩劈裂产生的多为台阶状脆性断裂纹,岩石细观成分对岩爆有较大的影响,结晶程度高、结构致密的硬脆岩石更易发生岩爆。
但是目前的研究中关于扫描电镜(SEM)图像的描述以定性为主,岩石作为一种天然材料,内部含有大小不同的孔隙和层次多样的微裂纹,具有一定的分形结构[7,12-13],且岩石从小尺度微断裂到大尺度整体破坏的损伤发展是一个分形过程。近年来,研究人员开始将分形理论应用到岩石力学当中,如彭瑞东等[14]通过带SEM的伺服试验机对岩石进行拉伸实验,得到分形维数可作为岩石表面细观形貌的参数。黄冬梅等[15]应用分形几何原理对大理岩单轴压缩下的破坏裂纹细观图像进行计算,得出断口的分形维数与破坏荷载之间有一定的关系。但综合现有文献资料,对岩石损伤细观裂纹的分形特征研究仍较少,对于砂岩弯曲荷载下的断裂破坏细观描述则更为少见。
本文以某煤矿关键层砂岩为研究对象,对砂岩施以不同加载速率的弯曲荷载直至断裂,分别对弯曲断裂破坏面细观结构进行扫描电镜观察,对其细观形态和微破裂形式进行分析,利用分形理论计算扫描电镜下的裂纹分形盒维数,分析不同加载速率下砂岩弯曲折断破坏面的分形特征,分析砂岩弯曲破裂面分形维数与加载速率之间的关系,为研究顶板破断而引发的动力灾害机理提供理论支持。
1 砂岩三点弯曲实验
1.1 实验样品
本实验采用的砂岩为淡褐色细粒砂岩,经实验分析,全岩样品矿物中石英、长石、云母、黏土矿等的质量分数分别为59%、16%、10%、15%。从取样点采集完样品后,运送至实验室,精加工成符合标准的样品,试件表面平整,各边互相垂直,标准尺寸为50 mm×50 mm×250 mm的长方体,尺寸误差为±0.3 mm,无预制缝。
1.2 三点弯曲实验
实验采用WDW-50微机控制电子万能试验机对样品进行三点弯曲实验,实验前对该试验机进行标定、设置,并在底部承压端两侧设置支撑底座,底座为圆柱形,支点跨距为200 mm。采用负荷控制方式进行加载,在砂岩长轴中央施以弯曲荷载,分别选取0.1、0.4、1、10、30、60 N/s的加载速率对6组样品进行连续加载。实验前先将电子万能试验机的压头与试件中部轴线上放置的圆柱形细钢件轻微接触,保证加载系统与试件为线接触,且在试件中央。每组3个试件,匀速加载直至试件破断,记录各试件的破坏荷载,实验结果离散性大则增加样品,所有实验数据如表1所示,选取离散性小的3组数据取平均值进行分析,各组数据误差棒如图1所示。
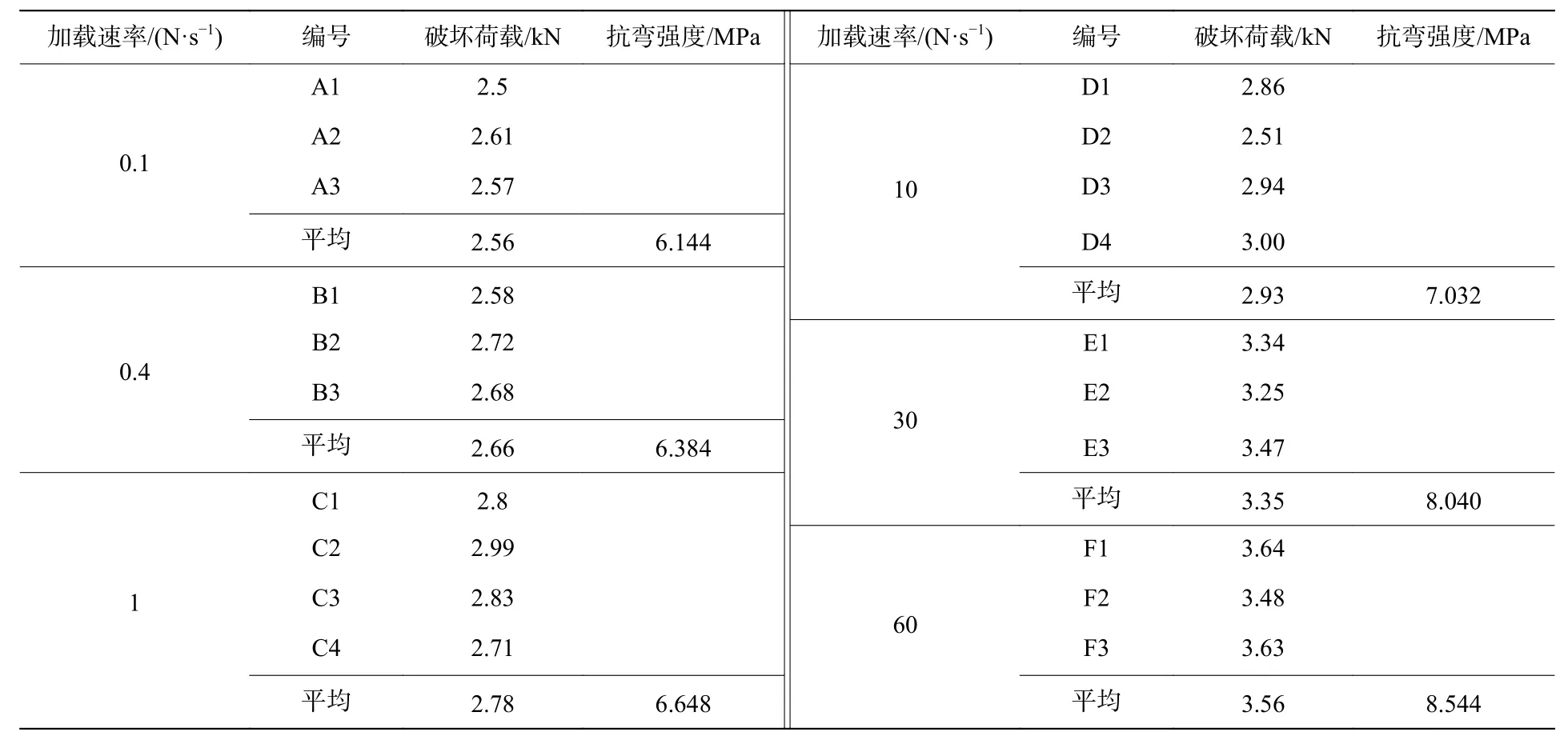
表1 岩石三点弯曲实验力学参数Table 1 Mechanical parameters of rock three-point bending testing
实验得到各组的弯曲破坏荷载,可计算出岩石在该加载速率下的抗弯强度:

式中:Rt为试件抗弯强度,Pt为试件弯曲破坏荷载,L为弯曲跨度,a为长方体断面宽,b为长方体断面高。
图1显示,在实验的加载速率范围内,不同加载速率下砂岩弯曲破坏荷载(或抗弯强度)并非恒定,而是与加载速率有关的变量,随加载速率的增大破坏荷载(或抗弯强度)呈正相关增大,具有显著的加载速率效应,随着加载速率增大,岩石损伤和灾变相对滞后,样品破坏荷载(或抗弯强度)较高,岩样在高速加载条件下的损伤具有一定的时滞性。
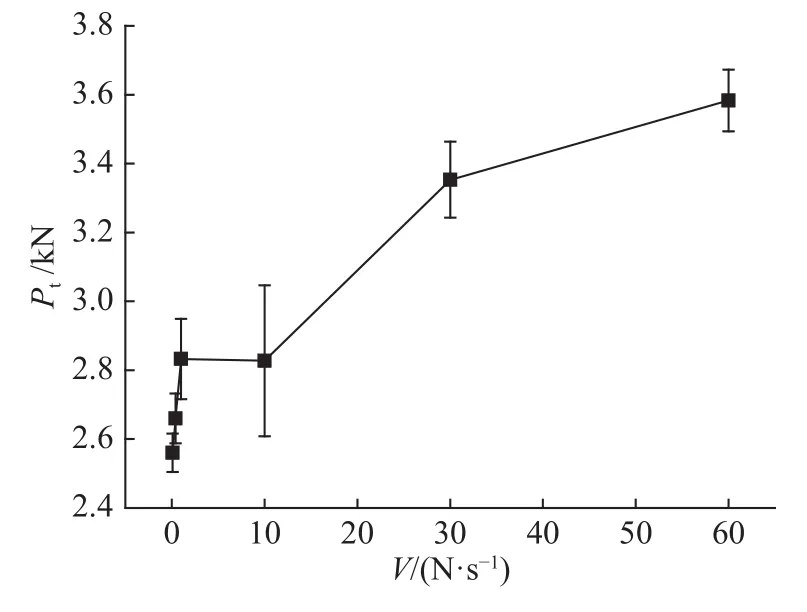
图1 破坏荷载的加载速率效应Fig.1 Loading rate effect of failure load
1.3 不同加载速率下样品破坏特征
实验采用6级加载速度,对不同加载速率下岩样破坏形式和特征进行观察和记录。
加载速率较慢时(0.1、0.4、1 N/s),样品在完全破裂前出现破裂声,下部裂纹显现并迅速发展至完全断裂;加载速率较高时(10和30 N/s),样品下部裂纹的扩展情况无法用肉眼观测到,样品直接脆断,样品破裂宏观上无任何先兆表现;加载速率升高至60 N/s时,样品的破坏形式更剧烈,样品破断声更大,并有少量碎屑从样品下部断口处崩出,断裂口亦较大,如图2所示。

图2 0.1、10和60 N/s加载速率下样品破坏照片Fig.2 Specimen destruction under loading rates of 0.1, 10 and 60 N/s
2 扫描电镜实验
2.1 样品
本文主要利用二次电子成像对砂岩弯曲断裂破断面进行裂纹特征分析。选取三点弯曲实验中各加载速率下断裂的岩样,确定弯曲断裂面为观察面。由于样品起裂点损伤区更大,且脆性岩石裂纹发展较快,裂纹孕育时间较长,因此选取靠近起裂点的样品底部位置为主观察区,用切割机将断面切割成1 cm×1 cm的小薄片,厚度不超过0.5 cm[16]。实验采用FEI Quanta250环境扫描电镜,挑选切割较为平整的样品块顺次放置于样品台上,用导电胶粘好,并对样品进行喷金处理,以增加岩样的导电性。
2.2 砂岩断口特征分析
在扫描电镜上对实验样品不同部位进行不同放大倍数下的观察,先将放大倍数调至50倍,选择裂纹集中的区域进行进一步观察并拍摄扫描电镜照片,分别进行100、200、400倍拍摄,依次选取多个观察点进行拍摄比较,得到不同速率下砂岩断口SEM图,见图3。
由图3可以看出:砂岩内部结构较复杂,主要由各种砂粒胶结而成,黏土杂质含量较高,并含有大量微裂隙和杂质;砂岩弯曲荷载作用下的破裂面断裂形式为沿晶断裂(IG)和穿晶断裂(TG)耦合,整个断面呈现凹凸不平的形态,加载速率较低时,砂岩中沿晶断裂为主要破坏形式,相应的砂岩抗弯强度也较低;而中高速加载时,砂岩穿晶断裂比例明显上升,且穿晶裂纹趋于复杂,砂岩的弯曲破坏荷载呈现一个陡增的趋势,所需断裂能也随之升高。从岩矿结构角度解释,矿物沙粒之间无序紧密镶嵌,当某矿物受力时,必然牵动上下左右相邻矿物且相互传递,在接触胶结最弱部位产生绕晶微裂隙,随着加载速率的增加岩样内部沿晶微裂隙的扩展速度跟不上加载速率,未能进一步扩展,试图发生穿晶破裂,从而减缓了岩样的破坏速度,进而岩样的破坏荷载也随之提升。

图3 不同加载速率下样品的SEM图像Fig.3 SEM images of samples at different loading rates
对各加载速率下的砂岩断口样品的100倍电镜图样进行分析可得:0.1 N/s速率下的砂岩断裂模式以沿晶断裂为主,占90%以上,鲜见穿晶断裂,可观察到表面颗粒沉积硅质球;0.4 N/s速率下,沿晶断裂占80%左右,沿原有裂隙开裂的位置可观察到黏土矿物颗粒;当加载速率继续升高至1、10、30 N/s时,穿晶断裂占比也随之上升,达到40%~50%,并伴有部分解理断裂;加载速率为60 N/s时,穿晶断裂明显增加,且穿晶断裂面随之增大、聚集,断裂面也较之低加载速率下的更粗糙,可见明显的河流状和阶梯状裂纹,沿晶断裂只占到30%左右。由此可见,加载速率能在一定程度上影响砂岩弯曲折断的断裂形式,加载速率较低时,以沿晶断裂为主,随着加载速率的提升,穿晶断裂比例逐渐上升。
通过分析砂岩弯曲断裂断口形貌, 可知砂岩弯曲断裂的细观机制主要是在拉伸作用下岩石的脆性断裂。低速加载下,断口多在胶结处及薄弱晶间断裂;高速加载下,则出现部分河流状解理断裂,不同弯曲加载速率下的断裂均表现出较强的拉伸脆断特征。
3 砂岩弯曲破裂细观裂纹分形分析
3.1 细观裂纹处理
根据图3扫描电镜图像可以发现,穿晶断裂、微裂隙、孔隙的部位颜色相对较深,呈现黑色或深灰色,而穿晶断裂部分则颜色较浅,为浅灰色或白色。利用Photoshop图像处理软件对400倍下扫描电镜图像进行处理,将原灰度图通过寻找最优阈值合理转化为二值图,再对图像的亮度和对比度进行调整,反相后消除裂纹以外的干扰项,仅保留图像中的裂纹信息,提取只有黑白两色的裂纹信息图片。灰度处理过程图如图4所示:将原始扫描电镜图像图4(a)经过Photoshop处理得到图4(b),进而对图像进行反相处理得到图4(c),根据原始图像去除岩石晶粒、晶面暗域等不必要的信息,保留所需裂纹信息图像,并用Matlab描边进一步去除冗余信息后填充得到处理后裂纹图片图4(d)。
3.2 细观裂纹分形计算
分形几何是由Mandelbrot发展起来的[16],用来描述自然界的不规则和杂乱无章的现象和行为。而岩石断口轮廓具有一定的统计自相似性,岩石破裂断口分布的分形维数是岩石细观结构、加载方式及样品形状尺寸等因素的综合反映。
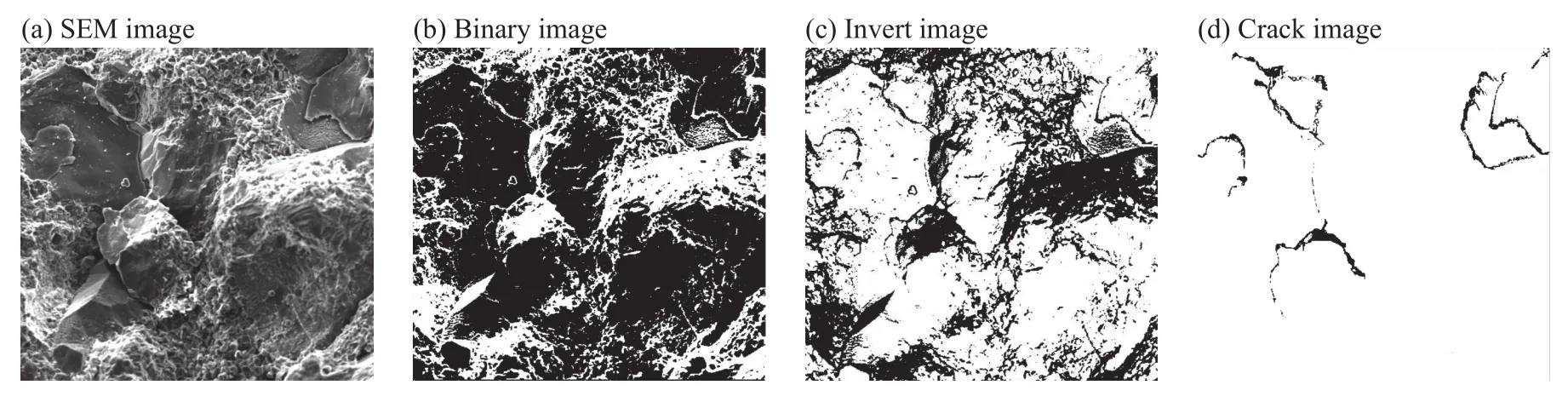
图4 SEM图像裂纹图像提取过程Fig.4 Crack image extraction process of SEM photos
目前用于材料断裂表面分形维数的计算方法有很多种,如周长-面积关系法、幂律谱法、自仿射分形法、盒维数法和Hausdroff维数法等[17]。其中盒维数法相对较为直观,易于进行程序化计算,且对图像的几何自相似性要求并不是很严格,得到了广泛应用,因此本文选取盒维数法进行计算。
盒维数分形法的定义为:设有边长为a的封闭盒子,有序排列覆盖在已有的二值化图像之上,盒子之间互不重叠,对内部包含黑色内容的盒子进行计数,总数记为N(a),当a趋向于0时,该极限值即为该图像的盒维数分形维数D:

式中:D为盒维数法计算得到的分形维数,a为盒子的尺寸。实际应用中,盒子的边长a只能取到有限的值,故通常利用最小二乘法对log(1/a)和logN(a)进行拟合,得到:

式中:斜率Ds即为盒维数法计算得到的分形维数值。
基于上述分形盒维数计算原理,利用Matlab数据处理平台进行编程,对处理后得到的二值化裂纹图像进行分形盒维数的计算。SEM图片经处理后的二值化图像是由一系列的像素点组成,可以看作是一个m×n的数值矩阵,在同一图像中以一个像素点为最小盒子,选取512×512像素区域,统计不同尺度下包含黑色像素的盒子个数N,计算logN和log(1/a),即可开得到相应的关系式。
在各加载速率下选取3张不同部位的电镜图进行处理,并求取平均值以减少误差。图5为0.1 N/s速率下3张样品裂纹图片经处理后得到的拟合直线及斜率,其分形维数即为斜率的绝对值。继续根据式(3)对图像裂纹信息进行线性拟合得到表2。
根据表2所示,砂岩的裂纹分形维数随加载速率的升高而逐渐增大,根据分形维数的概念,裂纹分形维数越大,说明裂纹越曲折复杂,裂纹越长或越宽,宏观上产生单位面积的裂纹所消耗的能量就越大,相应的,裂纹扩展所需的能量也越高[18]。因此,随着加载速率的增加,岩石的裂纹缺陷也随之增加,微裂纹在表面的占比也越高,可见砂岩损伤程度随之加深。分形维数与加载速率之间的关系如图6所示。
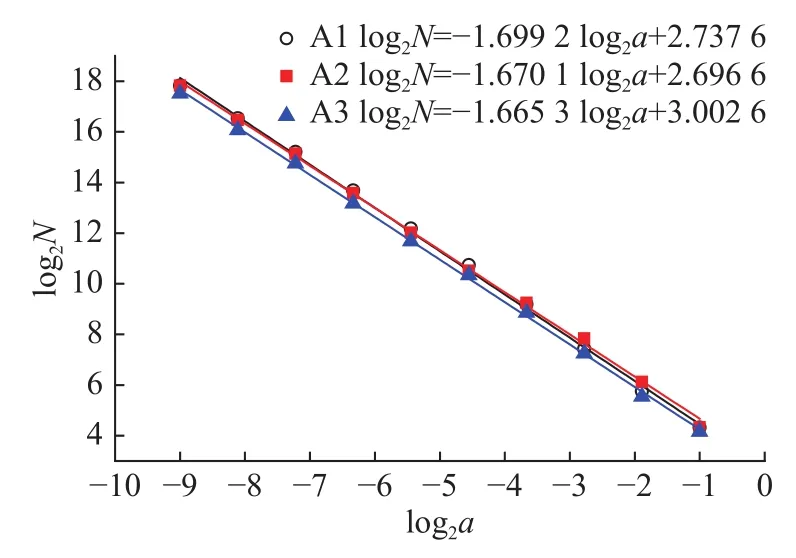
图5 分形盒维数法计算Fig.5 Fractal dimension calculation in box counting
由图6分形维数和加载速率图像可得,砂岩断裂面裂纹分形维数随加载速率的增量并不是一个常数,而是呈幂函数分布,对分形维数Ds和加载速率V进行拟合,得到函数关系式为(R2=0.949 88):

从总体趋势可见,加载速率越高,弯曲破坏荷载、抗弯强度越大,形成的弯曲破坏分形维数也越大,砂岩弯曲破断细观裂纹分形维数与加载速率有一定的关系。
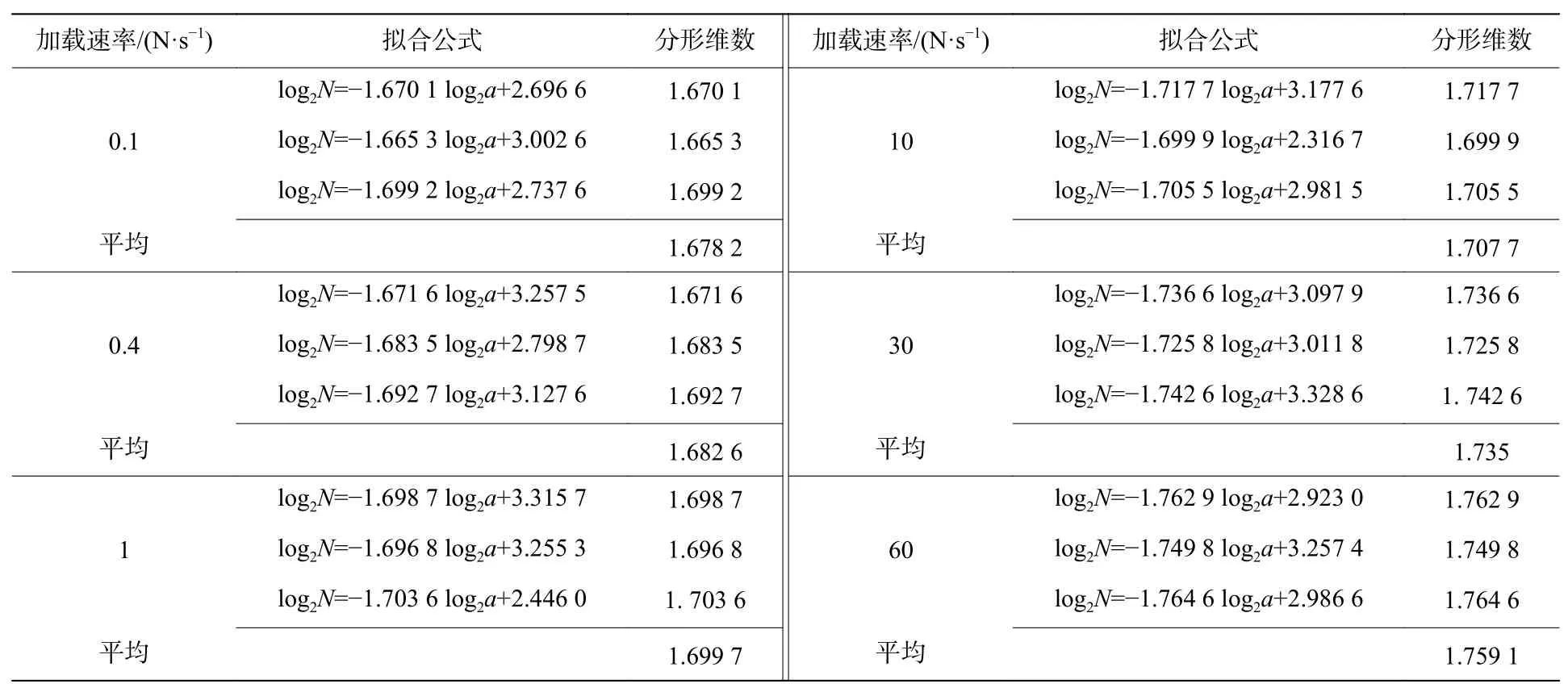
表2 砂岩试件裂纹分形维数Table 2 Fractal dimension of cracks of sandstone
砂岩弯曲荷载分形维数值与弯曲破坏荷载、抗弯强度呈正相关,如图7所示0.995 97),在本实验的加载速率范围内,弯曲破坏荷载越大产生的弯曲破裂分形维数值就越大,说明加载速率越快所积累的应变能越大,裂纹扩展所需能量越大,一旦发生断裂突然释放的能量也越大。因此,高速加载下,宏观上表现为岩石样品断口下端出现类岩爆现象。
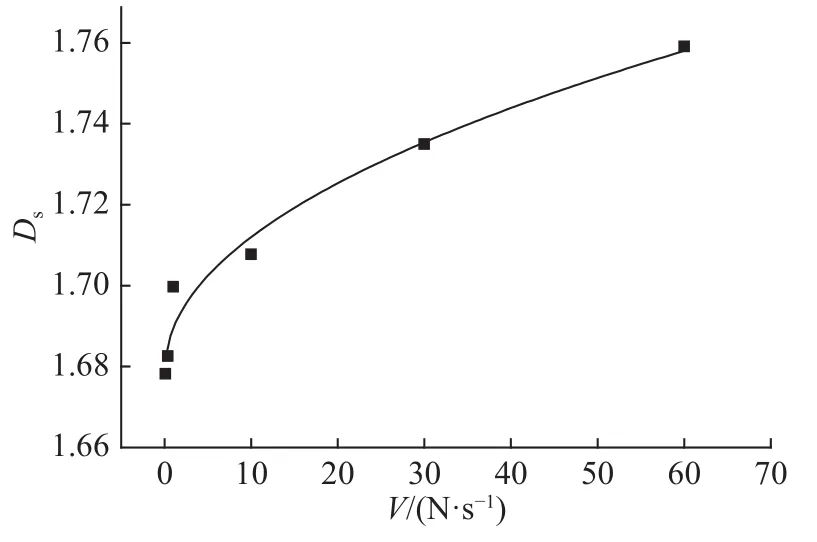
图6 加载速率和分形维数之间的关系Fig.6 Relationship between fractal dimension and loading rate

图7 破坏荷载(Pt)、抗弯强度(Rt)与分形维数(Ds)的关系Fig.7 Variation of failure load (Pt) and bending strength (Rt)with fractal dimension (Ds)
4 结 论
(1)砂岩三点弯曲实验显示,弯曲破坏荷载及抗弯强度随加载速率的增大而逐渐增大,岩样破坏过程的力学行为和加载速率有关,岩石弯曲破坏存在时间效应。
(2)低加载速率下,砂岩宏观断口较整齐;高速加载下,断口下端则部分呈现类岩爆现象,有碎石崩出。观察SEM图片,可见随着加载速率的增大,砂岩穿晶断裂的比率明显升高,裂纹趋于复杂,加载速率对砂岩的断裂方式有一定的影响。
(3)砂岩断裂方式主要为穿晶和沿晶断裂耦合,但沿晶断裂的占比相对较高。砂岩弯曲断裂的细观机制表现为拉伸作用下的脆性断裂。
(4)砂岩弯曲断裂破坏裂纹分形维数随加载速率的增大而逐渐增加,且与弯曲破坏荷载、抗弯强度呈正比,加载速率越快,破坏时释放的能量也越大,因此采矿速度是导致岩体动力灾变释放能量大小的因素之一,降低岩体能量释放,可从控制开采速度着手。
