基于分布式偏好信息的不确定性多属性决策方法

张孝琪

(安徽工程大学 管理工程学院，安徽 芜湖 241000)

在实际决策过程中，由于信息大多数具有不精确、模糊等特征，加上决策者对问题认识的局限性或自身知识的缺乏等原因，决策者获取的决策属性值和属性权重值大多数是不确定的。描述这些不确定的属性值信息和权重值信息常用的形式有：区间数、三角模糊数、语言评价值等等[1-3]。分布式偏好信息能够充分刻画不精确、模糊的决策信息，它通过评估等级与隶属于等级的概率来联合描述不确定性信息[4]，自提出以来在决策领域得到广泛关注，已逐渐成为多属性决策研究中的一个热点。相关学者对此纷纷展开研究，取得了一些研究成果，大致可以分为两类：第一类研究是通过分布式偏好信息构造类似于层次分析法(Analytic Hierarchy Process,AHP)中的模糊判断矩阵来进行决策。如付超[5]等利用分布式偏好信息表示方案间两两相互比较关系，并将其转化为得分值区间，然后通过一致性直觉判断矩阵的决策方法来进行排序。常文军[6]等提出具有一致性的两两方案间分布式偏好信息矩阵，并结合可能度法得到排序结果；另一类研究是将分布式偏好信息作为决策属性下的评估信息，进而构建出传统多属性决策方法中的决策矩阵，然后通过属性权重对决策信息集结后进行决策。如习扬[7]等将在线评价信息化为分布式偏好信息，研究了不完全信息下权重确定问题。Gong[8]等以区间数权重为决策变量，将证据推理方法(Evidential Reasoning,ER)和DEA交叉效率(DEA Cross-efficiency)方法相结合，分析和探讨决策方案存在竞争关系的排序问题。Wang[9]等将分布式偏好信息用于桥梁风险评价并进行排序。

上述诸多方法从不同的视角研究了含有分布式偏好信息的多属性决策问题，模型和方法在很多情况下具有较好的适用性。但是目前研究还存在某些局限性，如第一类方法在处理含有大量决策方案时，决策者需要进行很多次的相互比较，判断矩阵的一致性问题难以保证；第二类方法采用非线性信息融合方法，计算过程较为复杂，而且算法中还需要确定的权重信息，在面对权重信息未知或者部分已知的情况下需要结合其他方法方可进行决策。为此，为减少决策的复杂程度，在第二类方法的基础上，提出一种不完全信息下基于分布式偏好信息的多属性决策方法。

1 决策问题

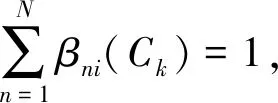
决策问题是：在权重完全未知或者部分已知情况下，如何利用分布式偏好信息对决策方案集进行充分排序。

2 决策方法

2.1 属性优势度计算

为了实现不同分布式偏好关系的有效比较，按照文献[5]的思路将分布式偏好信息转换为效用值区间，并利用区间数距离进行比较，得到属性的优势度[10]。对于某个属性Ci，其效用值区间得分[umin(Ci),umax(Ci)]可由式(1)表示：

(1)

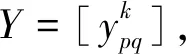
2.2 决策方法与步骤

针对权重完全未知和部分已知的情况，不同学者提出了相应的处理方法。在多属性决策中，对于权重完全未知的情况，相关研究多采用主观赋权、客观赋权、主客观赋权结合等方法[11]。这类赋权方法在不同情况下具有较好的实用性，但是也存在着一些弊端，如不同赋权方法得到的最优权重可能不同，进而可能导致决策结果发生变化，决策者在方法选择上存在困惑；对于权重部分已知的情况，相关研究多通过建立线性或者非线性规划模型来求解出最优权重，这类方法适用范围也有限，不能有效处理某些特殊情况的权重信息，如权重在约束外围内呈正态分布的情况。为解决上述两类方法存在的不足，用SMAA-2方法仿真模拟在权重约束下的最终效用值。SMAA-2方法是Lahdelma等在最初SMAA方法的基础上于2001年提出的决策方法，它是一种通过概率分布来近似描绘各种不确定形式的属性权重和属性值信息[12-14]。自提出以来，在设施位置选择、水库防洪调度等领域得到广泛应用[15-16]。

其主要思想为：随机生成某种符合权重约束的随机数权重，根据优势度矩阵得到各决策方案的整体优势度，并进行评价，经过多次迭代，利用统计学思想，得到决策方案排名第一或者其他名次的最优权重集和排名概率，依据排序权重得到最终的排序结果。具体SMAA-2方法如下：

基于随机生成的属性权重，决策方案Im的排名位置可由式(2)表示：

(2)

其中，u(Im,wm)为决策方案Im在权重偏好wm下的效用值，这里效用值由优势度来代替。假设决策方案排名最优名次为1，最劣名次为K。ρ(ture)=1;ρ(flase)=0。决策方案Im处于第k名时，此时的优势权重区域可由以下式(3)表示：

(3)

SMAA-2方法为决策者提供了多种辅助评价技术对各决策方案进行分析。

(4)

(5)

(6)

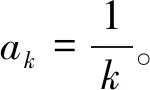
综上所述，给出不完全信息下基于分布式偏好关系的决策步骤：

Step 1:决策者根据专家意见或者在线评价系统，得到分布式偏好信息：各属性下的评价等级以及隶属度。

Step 2:将分布式偏好信息转化为区间得分，进而得到优势度矩阵。

Step 3:根据给定的权重分布情况，随机生成符合条件的权重，结合优势度矩阵，根据式(6)计算各决策方案的效用值，排序并标记名次。

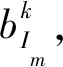
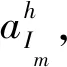
3 算例分析

根据文献[17]的数据和文献[18]的方法来说明该方法的有效性和可行性。从5家公司I1,I2,I3,I4,I5中选择投资对象，有4个评价准则：应对潜在风险能力C1、成长能力C2、未来持续盈利能力C3、经营环境C4。指标权重信息不完全：0.12≤w1≤0.20，0.12≤w2≤0.40，0.08≤w3≤0.25，0.10≤w4≤0.23。评价等级为7级，Hn=(H1,H2,H3,H4,H5,H6,H7)，对应的等级效用分别为(0.05,0.13,0.25,0.40,0.57,0.77,1)，决策矩阵如表1所示。根据上述决策步骤求解投资对象选择问题。

表1 被选企业的决策信息矩阵

利用式(1)将决策信息矩阵转化为评价得分值矩阵：

分别计算不同属性下的优势度，构造相对优势度矩阵为：

由于指标权重信息部分已知，以公司I4为参考点，利用Matlab 2016a软件进行蒙特卡洛仿真，模拟10 000次，计算得出所有决策方案在不同排序位置的概率(如表2、图1所示)。

与文献[17-18]的结果进行比较，评价结果一致，验证了该方法的有效性与科学性。通过对比分析也显现出研究中方法的两个优点：一是方法充分考虑了所有可能的权重信息，有效地避免了通过求解具体的权重进行决策，结果具有鲁棒性；二是通过可接受度指数等指标可以得到丰富的决策信息辅助于决策。

在不确定性多属性决策过程中，会存在多种排序结果。尽管在上述算例中决策者可以依据总体可接受度得到较为鲁棒的决策方案排序，但是决策者还应该全面分析所有的排序结果及其出现概率如表2所示。为此，对以I3为最优决策方案的排序序列进行全排序仿真，得到全面详尽的排序结果。在理论上，5个决策方案可能有120种排序结果，上述算例中，I3,I4,I5的位置相对固定，因此，只有两种排序结果，其排序结果与排序概率如表3所示。

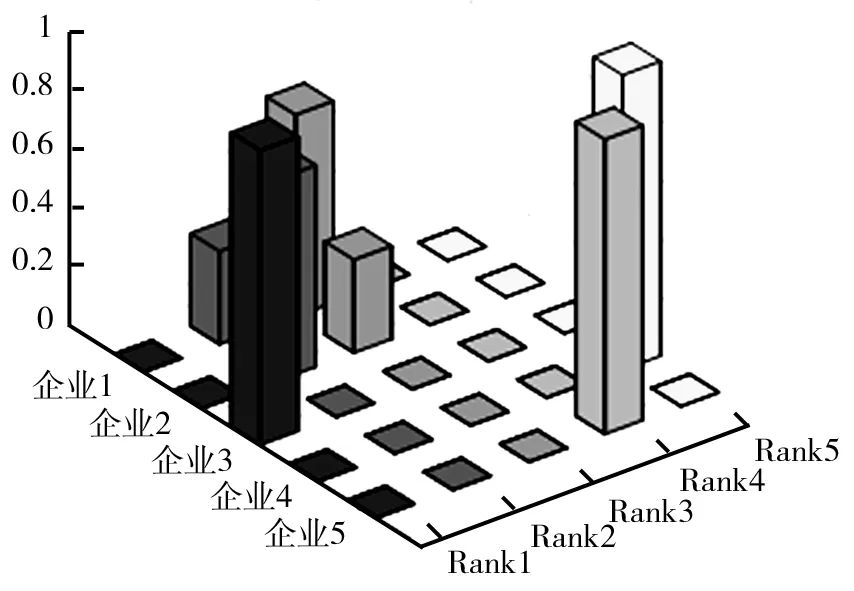
图1 不同排序位置上5个企业的可接受度

b1pkb2pkb3pkb4pkb5pkahImI100.31580.6842000.3859I200.68420.3158000.4474I3100001I4000010.2I5000100.25

表3 文献[14]、文献[15]方法与本研究中方法对比分析结果

4 结论

在多属性决策问题中，将分布式偏好信息转换成区间数，通过构造区间数的优势度，并基于SMAA-2模型提出一种不确定性多属性决策方法。该方法从仿真模拟的视角利用概率和分布函数去刻画属性权重的不确定性，并通过多次的模拟，得到不同排序位置的接受指数和总体可接受指数，进而得到鲁棒性排序结果。从算例看出，相对于其他传统决策方法，研究中方法提供的结果信息更为丰富，可以得到不同排序结果及其概率。分布式信息是基于确定值描述的，考虑区间数情况是下一步研究的方向。