基于GARCH族的VaR方法在上证市场中的风险度量

（新疆财经大学应用数学学院，乌鲁木齐市，830012） 张曼琳 王宇菲

1 引言

中国在2000 年加入WTO 以后，中国的金融市场逐步对外开放并且走向世界，随着经济全球化及投资自由化发展，我国金融市场的波动性日益加剧，金融风险管理已成为金融机构和企业管理的核心内容。VAR 理论用实际数据为投资者呈现出所面临的风险，在这些逐步成熟的理论指导下，我国股票市场的投资者也在积极使用并且改进风险管理方法，使得其自身在复杂多变的经济环境下能够有效规避风险，实现投资盈利。采用风险价值理论和实证相结合的想法，运用GARCH 模型和风险管理VAR 理论基于三种不同分布的假定下讨论了GARCH 类模型的VAR 计算哪个精准度最好，并从实际数据出发计算VAR值，研究结果对估计股市风险价值和投资者决策具有参考意义。

2 模型概述

2.1 GARCH模型

在金融理论模型里，扰动项 μt的条件方差会受到之前时刻变量的影响。描述资产收益率的波动性是需要精确的参数估计，其中容易受到约束条件的影响，GARCH 模型主要是针对金融数据的回归模型以及对波动性的分析研究，还可用来计算不同时期的波动形式，减少模型的复杂性，使结果看起来更加简单明了。

GARCH模型的基本原理：

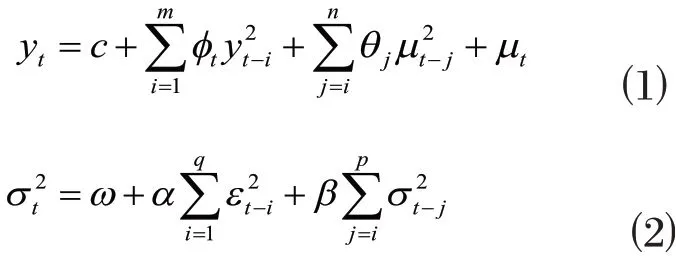
ω为常数项，p是GARCH项的最大滞后阶数，q是ARCH项的最大滞后阶数，α和β为系数。

与波动的聚集效应相同：伴随着较大的波动后可能是更大的波动，较小的波动后伴随着更小的波动，GARCH（p，q）模型是ARCH模型的扩展。

2.2 VAR模型

VAR（Value at Risk，在险价值）的定义是指在正常市场条件下给定了置信水平和持有期，某一金融资产或证券组合在未来的特定时期内的最大可能损失。用数学公式表示为：

其中 p( )表示资产价值的损失小于损失上限的可能概率，Δp表示资产组合在持有期内的价值损失量，c为既定置信水平。

3 实证分析

3.1 数据选取

对上证地产指数风险进行度量，采用Eviews软件对上证地产指数分析处理。选取2012年1月4日～2018 年4 月2 日的上证地产指数，共1 517 个样本数据。在实证分析前，对上证地产指数进行日对数收益率处理，计算出1 516个日对数收益率，表示为。其中 pt为上证地产指数的t日的收盘价；为 t -1日的收盘价。

3.2 数据分析

3.2.1 数据的统计特征

数据的基本统计特征如表1 所示。由表1 可知，上证地产指数日对数收益率偏度为-0.590 811，峰度为7.451 053，呈现出分布偏左现象，与之数据服从正太分布数值对比发现，上证地产指数日对数收益率有显著的尖峰后尾特征，不服从正态分布。

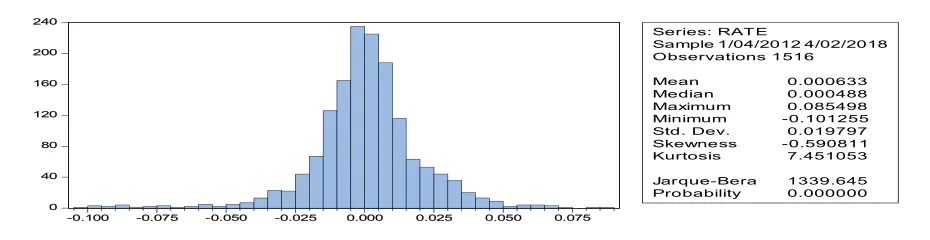
图1 数据基本统计特征

3.2.2 单位根检验

遵循AIC和SC最小原则，对上证地产指数日对数收益率进行ADF 单位根检验，结果如表1 所示。从表1 可知，ADF 的P 值为0.0 000，小于5%的显著性的临界值，满足数据平稳性要求，则说明上证地产指数日对数收益率序列是平稳的序列。

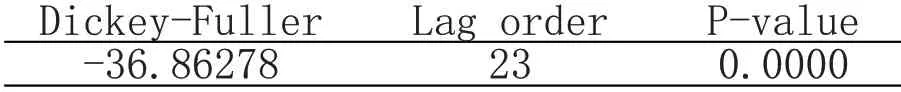
表1 地产指数日收益率自相关检验

3.2.3 自相关检验

对上证地产指数日对数收益率进行自相关检验，通过Eviews系统分析总结出上证地产指数36阶滞后的AC值和PAC值。P值接近零，高阶之后等于零，可见数据之间不存在明显的自相关，换句话说上证地产指数日对数收益率之间基本不存在自相关问题。（见表2）

表2 自相关检验结果

3.2.4 LM异方差检验

对上证地产指数日对数收益率的自相关检验，可以观察到指数的收益率滞后1阶存在自相关。

表3 地产指数日收益率ARCH模型

得到均值方程为：

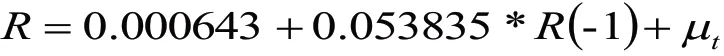
用Ljung-BoxQ 统计量对均值方程拟合后的残差及残差平方做自相关检验，结果表明残差不存在显著的自相关，而残差平方有显著的自相关。

图2 地产指数日收益率残差序列图

表4 地产指数日收益率ARCH效应检验

综上结果，AR(1)的参数值的P值小于显著性水平α，符合建立AR(1)模型。ARCH(1)的误差项进行自回归条件异方差(图2)，发现误差平方序列存在自回归条件异方差，从图2看出2017误差项年比其他年份比较波动幅度较小，2015 年中旬到2016 年初波动尤为突出，认为数据可以运用GARCH 模型进行分析。对序列进行ARCH 效应检验，从检验结果(表4)发现ARCH效应是显著的，说明上证地产指数日收益率序列可建立GARCH模型。

4 GARCH-VaR模型建立

对数据进行进本分析的记过可以判断出上证地产指数日对数收益率是平稳的，在不满足正态分布的同时不存在自相关，存在异方差并且具有ARCH 效应。利用Eviews 软件，对样本数据进行GARCH建模，可得表5：

表5 地产指数日收益率GARCH(1,1)模型检验

条件方差中ARCH 和GARCH 项都属于高度显著的，因此收益率序列具有明显的波动集簇性。其中ARCH 和GARCH 项系数之和为0.99＜1，则说明GARCH（1，1）过程是平稳的。经过ARCH-LM 检验，主模型不存在ARCH 效应（P 值为0.5 382，大于显著性水平）。所以样本数据模型均为GARCH（1，1）类模型。

（1）基于正态分布的GARCH 族模型参数。每个模型对应两行内容，第一行是模型参数值；第二行是Z 检验值（见表6）。由表6 可知，模型参数在5%的显著性水平都是显著的。由于常数项不影响效果的估计，故没有残留明显的异方差现象。这说明模型可以较好的拟合上证地产指数日对数收益率的异方差现象。 EGARCH 模型的系数γ=0.019491，即条件方差对冲击的反应是非对称的，根据模型的对数性质，可得出利好消息带给上证地产指数的波动比等量的利空消息更大，上证地产指数存在明显的杠杆效应。

基于GARCH 模型参数，计算得到VAR 的统计特征值及Kupiec 的检验结果（见表7），LR 值越小，说明模型的预测的准确性越高。在99%的置信水平下，通过正态分布GARCH 类模型得出的VAR 均值差别不大，最大值最小值分别差别也不大。由表7 可知，LR 检验的结果：在显著水平为1%的情况下，GARCH(1，1)、TARCH（1，1）和EGARCH（1，1）模型的LR 检验值显著小于6.635，通过了LR 检验，相对于没有通过检验的模型结果更加准确

（2）基于T 分布的GARCH 族模型参数。模型参数在5%的显著性水平下结果均较为显著，结果表明没有残留明显的异方差现象，因此模型可较好地拟合上证地产指数日对数收益率的异方差现象，并且从参数估计结果可以看出上证地产指数存在明显的非对称效应。

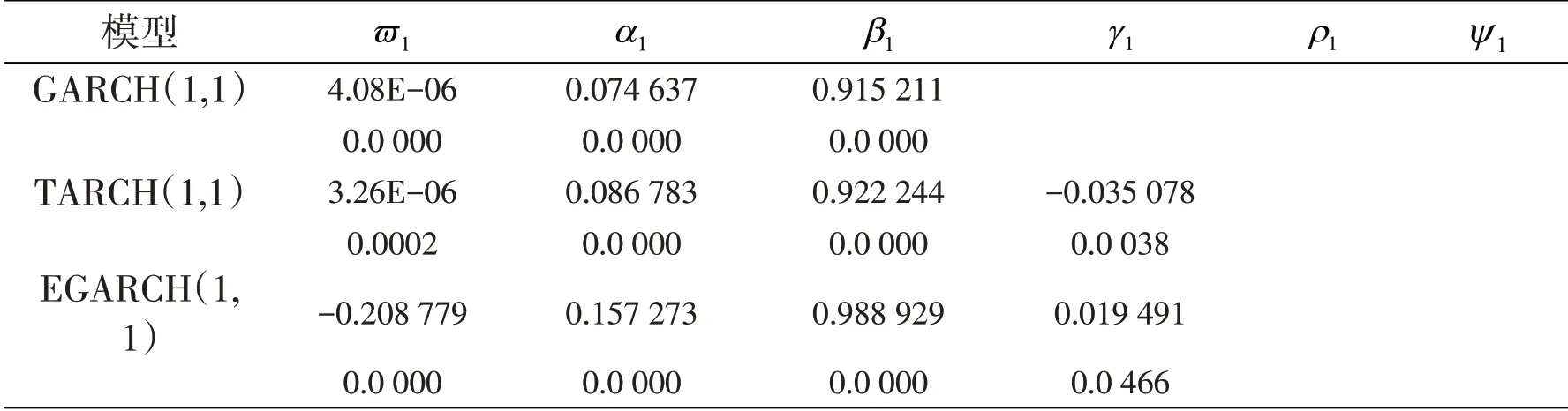
表6 基于正态分布的GARCH类模型参数值及Z值

表7 基于正态分布的GARCH类模型VAR返回检验值

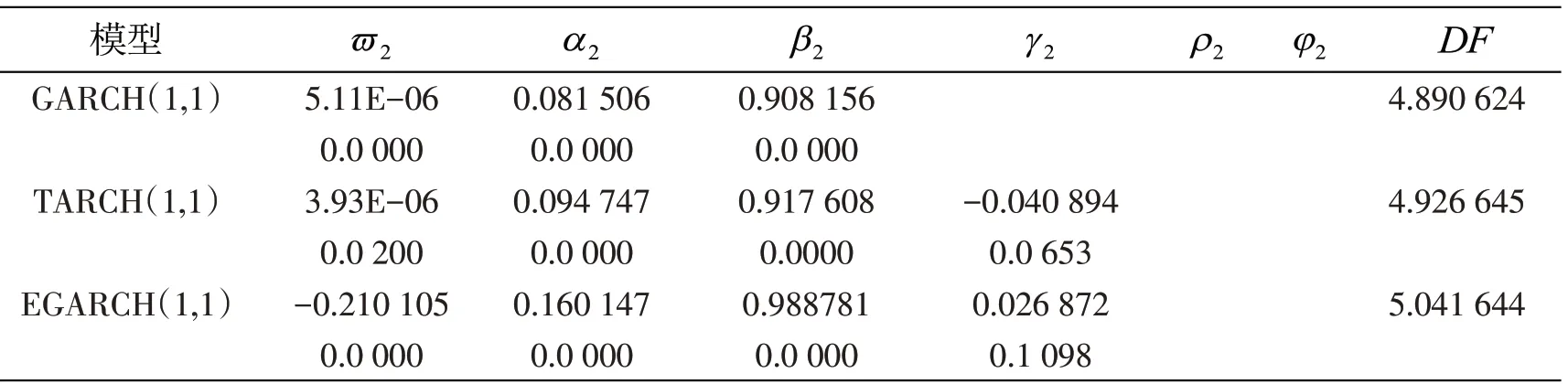
表8 基于T分布的GARCH类模型参数值及z值

表9 基于T分布的GARCH类模型VAR返回检验值

表10 基于GED分布的GARCH类模型参数值及Z值

由表9可知，在99%的置信水平下，各种计算出来的VAR均值之间差距不大。在1%的显著性水平下GARCH（1，1）、TGARCH（1，1）和EGARCH（1，1）模型的LR检验值均小于6.635，即在显著性水平在1%时接受原假设。基于T分布的上证地产指数计算出来的VAR 值结果都比较精确，说明GARCH（1，1）模型、TGARCH（1，1）模型和EGARCH（1，1）模型都能够比较好地拟合上证地产指数，并且其中EGARCH（1，1）模型LR 值最小，说明模型预测的准确性相对较高。

（3）基于GED 分布的GARCH 族模型参数。同样没明显的异方差现象，因此模型可较好地拟合上证地产指数日对数收益率的异方差现象，上证地产指数存在明显的非对称效应。GED 分布下个模型估值结果的尾部参数即V 值在1.24 上下波动，因此，相比较其他分部GED分布可以更好地刻画上证地产指数日对数收益率数据的厚尾特征。

基于GARCH模型参数在GED分布下计算得到VAR 的统计特征值及Kupiec 检验结果（见表11）。从表11可知，在99%的置信水平下，通过GED分布的GARCH 类模型得到的VAR 均值和最值差别不大，在显著性水平1%的情况下，TARCH（1，1）模型的LR检验值显著大于6.635；GARCH（1，1）和EGARCH（1，1）小于6.635，通过LR 检验，相对于没有通过检验的模型结果更加准确，说明上证地产指数日对数收益率在服从T分布时是不合理的。

5 结论

VAR是风险管理理论的最新发展，它能够综合反映市场各方面的风险状况，VAR理论用实际数据为投资者呈现出未来面临的风险度量结果，使得投资者在复杂多变的经济环境下能够有效地规避风险，实现投资盈利。选取上证地产指数分别在正态分布、T分布、GED分布假设下，运用GARCH类模型计算VAR值并进行Kupiec检验，对上证指数市场风险进行度量，对比分析在1%的显著性水平下的计算结果得到以下结论：

表11 基于GED分布的GARCH类模型VAR返回检验值

（1）分析上证地产指日对数收益率序列统计特征，得出上证地产指数日对数收益率有显著的尖峰厚尾特征，不服从正太分布，并且数据波动呈现出聚集性和持久性。

（2）正 态 分布 下 采 用GARCH（1，1）模 型、TARCH（1，1）模型和EGARCH（1，1）模型计算VAR值时得到的结果较为准确；基于T 分布的上证地产指数使用GARCH族模型计算出的VAR值得到的结果相对于正态分布下得到的VAR值更加准确；GED分布下采用GARCH（1，1）模型和EGARCH（1，1）模型计算VAR值得到的结果较为准确。三类GARCH模型计算得到的VAR 值、失败率、失败天数、VAR标准差和最值的差距都不大，并且EGARCH（1，1）模型在三种分布下都通过LR 值检验，模型的预测准确性相对其他三类GARCH模型较高。相对以上三种分布下，T分布下计算出的VAR值的失败率小于正态分布下计算出VAR值的失败率，更接近显著水平1%，虽然在99%置信水平正态分布和T分布下计算出的VAR值都通过了LR检验值，但秉着LR值越小、模型预测的准确性越高的原理，上证地产指数在T 分布下计算得到的VAR 值的结果相对精确性高。

（3）上证指数市场存在明显的杠杆效应及波动的非对称性，从模型参数可得出利好消息带给上证地产指数的波动比等量的利空消息更大，即正的冲击带来的波动大于负的冲击。

（4）在实际的投资决策过程中，投资者应根据理论基础选择投资观念，上证指数市场的杠杆效应提醒投资者需要理性投资，同时要考虑实际情况定制最优投资方案。