高速铁路网络复杂特性及其传播动力学研究

叶玉玲，李文卿，张 俊

(1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.广东省建筑设计研究院，广东 广州 510010)

近年来，高速铁路逐步形成网络化运营，高速铁路网络密度提高，整个网络上的节点和线路相互之间的关联性不断加强.研究高速铁路网络的拓扑结构和复杂特性，以及突发事件在网络上的传播扩散过程和影响机理，能够从突发事件预防的角度深入了解路网的性能，提高高速铁路应对突发事件的能力，保障整个路网的安全，为铁路部门建立应急预案提供科学依据.

随着复杂网络理论及其传播动力学的兴起，国内外学者对铁路和城市轨道交通等领域运用其方法来研究各类交通运输网络的结构特征，分析其复杂网络特性.Sen等[1]对印度铁路网络进行研究，得出该网络是具有小世界性质的无标度网络；Li等[2]统计分析中国既有铁路网络也具有无标度性质和小世界性质；叶婷婷[3]分析了全国既有铁路网络的静态统计特征，认为全国既有铁路网络的度分布可以用幂律函数拟合，与无标度网络相似；王伟等[4-5]从基础设施、列车停靠等多个角度构建了我国既有铁路的地理网和运输网的网络结构模型，并分析了这些网络的静态特性；张姝彬[6]对我国货运网络进行研究，得出地理网趋向于树状网络，而车流网的小世界性和无标度性都表现得更加明显；张兰霞等[7]对高速铁路网络进行研究，得出我国高速铁路服务网同样具有无标度和小世界性质.同时，对于传播动力学在轨道运输管理领域的应用研究上，张雅琴[8]将经典的传染病SIR(susceptible infected recovered)模型引用到铁路列车晚点研究中，得出在目前既有铁路网络的规模条件下，列车晚点一般只会造成初始晚点车站及其周边区域性的晚点；李朴[9]研究城市轨道交通大客流在网络上的传播特征，运用SIR模型进行分析，提出中间站与换乘站客流拥堵传播速度不同；吴璐[10]也引入SIR模型研究城市轨道交通网络中突发客流的传播扩散情况，得出传播速度主要取决于初始突发客流车站的最大客流处理能力.

国内外学者对于轨道交通网络拓扑结构的研究，一般都采用以实际信息进行抽象的方式对结构特征进行统计分析，得出相应的参数特征值，这对本文进行高速铁路网络拓扑结构具有一定的参考价值.而传播动力学作为新兴学科，目前涉及到轨道交通领域的研究，都是直接应用经典的SIS(susceptible infected susceptible)或SIR模型，没有考虑到这些经典模型的适用情况为均质网络，其假设条件并没有将网络的复杂特性与传播模型相结合.研究突发事件在高速铁路网络这一具有自身特性的拓扑结构中的传播影响规律，将是本文的研究重点和创新所在.

1 高速铁路网络模型的建立

根据《中长期铁路网规划(2016年版)》，我国将建设形成以250 km·h-1以上的“八纵八横”主通道为骨架、200 km·h-1及以下的城际铁路为补充的高速铁路网.所以，本文研究所选取的数据包括全路所有D、G字头列车和C字头列车及相关客运站.

将全国高速铁路抽象为由车站、线路和运行列车所构成的复杂网络拓扑结构.抽象后的高速铁路网络以2017年第二阶段调图后开通的全路707个高铁车站、线路及列车运行组织关系为基础.在未来，随着更多新建线路的开通，高速铁路网络也会有一定变化，运行图也会随之进行调整，因此在未来可能的计算分析中，可以将之前构建的高速铁路网络邻接矩阵进行修正，若存在新线路及列车能够连接以前不相连的2个车站节点，则将原矩阵中的0变为1，表示2个节点间存在边，然后再使用更新修正后的邻接矩阵进行计算.

1.1 高速铁路物理网络

将车站作为节点，每2个车站间实际连通的线路作为边，构建高速铁路物理网络.物理网络是高速铁路提供旅客运输服务的基础设施和基本条件.由于高速铁路是复线运行，所以将物理网络看作无向网络模型.

为方便统计计算，将物理网络中的节点与节点间的边构建为邻接矩阵.物理网络由无向图Gp=(Vp,Ep)表示.其中，Vp={vp,1,vp,2，…,vp,n}，是高速铁路客运站的集合；Ep={ep,1,ep,2，…,ep,n}，是相邻车站间的线路集合；ap,ij表示节点vp,i和vp,j间是否存在边，可取值为0或1，由ap,ij构成矩阵Ap=(ap,ij)n×n，其中ap,ij取值如下：

(1)

1.2 高速铁路运输网络

将车站作为节点，任意2个站点之间只要有同一车次的列车分别停靠这2个车站，则将这2个车站相连并作为边，构建高速铁路运输网络模型.高速铁路运输网络也为无向网络模型，绝大部分列车车次在上下行停靠车站相同，个别列车上下行停靠车站有所不同时以上行列车停靠情况为主.

同样地，运输网络可由无向图Gt=(Vt,Et)表示.其中，Vt={vt,1,vt,2，…,vt,n}，是高速铁路客运站的集合；Et={et,1,et,2，…,et,n}，是同一列高铁列车经过车站间的连线集合；at,ij表示节点vt,i和vt,j间是否存在边，可取值为0或1，由at,ij构成矩阵At=(at,ij)n×n，其中at,ij取值如下：

(2)

2 高速铁路复杂网络特性分析

2.1 度及度分布

度是节点的基本属性之一，节点的度ki定义为与该i节点连接的其他节点的数目，也即该节点连接的所有边数之和.网络中所有节点的度的平均值称为网络的节点平均度.节点的度分布用分布函数P(k)表示，它表示某一节点有k条边的概率.

在物理网络中：度数为1的车站为线路的起始、终点站；度数为2的车站最为普遍，代表着两端各连接1个其他车站的大多数中间车站；度数为3及以上的车站连接了2条或2条以上的线路，旅客可以在这些车站进行换乘.经统计，度数最大为7，最小为1，平均度数为2.17，具体度数及其分布统计见图1.度数最大的3个站点分别是武汉站、南京南站及郑州东站，代表其所在城市在高速铁路网络中具有明显的交通优势.度数为2的车站在所有车站中所占比例最多(约为3/4)，表明当前单条线路通过的普通中间车站在网络中仍占绝大部分.

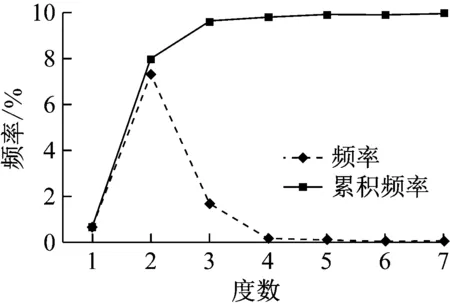
图1 高铁物理网络节点度分布情况Fig.1 Node degree distribution of HSR physical network

对物理网络的节点累积度分布取双对数进行拟合，所得图形如图2所示.双对数坐标下拟合曲线近似为1条斜向下的直线，符合幂律分布的特征.

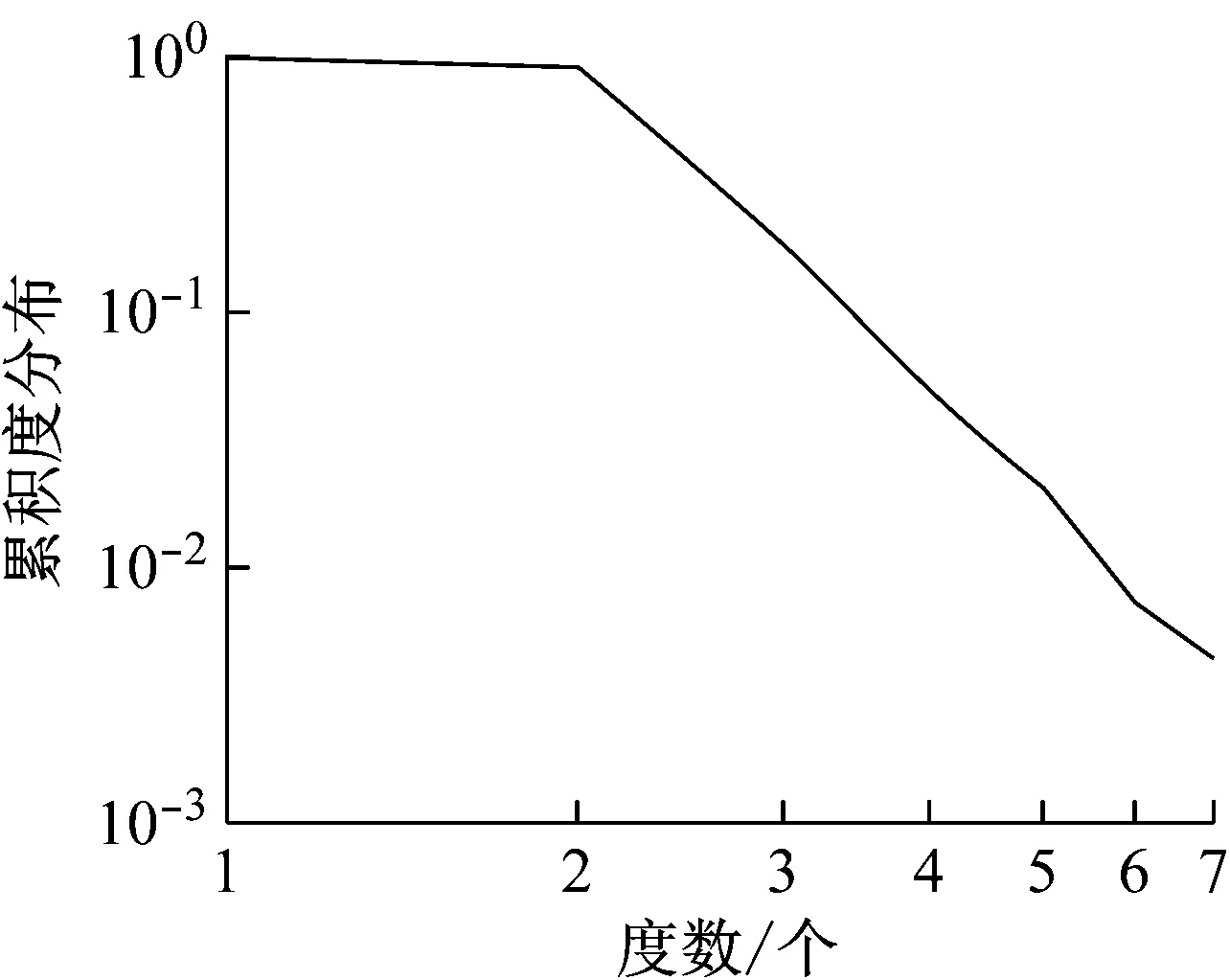
图2 高铁物理网络累积度分布双对数拟合Fig.2 Bi-logarithmic fitting cumulative degree distribution of HSR physical network

在运输网络中：节点是否相连取决于2个车站间是否存在列车开行往返2个车站，且在2个站均停站办理旅客上下车作业.若某节点的度数为k，则表示旅客从该车站乘车可以直接前往k个其他车站而不需要在途中进行换乘.运输网络度数分布统计如图3所示，平均度数为72.33，即网络中任一车站平均可以不需换乘直接乘车到达约73个其他车站.度数最大的车站为上海虹桥站，旅客从该站出发可以直接前往整个网络中大约50%的其他车站；其次是南京南站、武汉站和郑州东站.

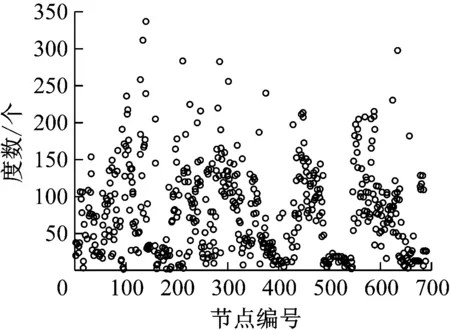
图3 高铁运输网络节点度情况Fig.3 Node degree distribution of HSR transportation network

图4显示双对数坐标下运输网络的节点累积度分布情况，其分布更近似1条曲线而非1条直线.表明其节点度累积分布符合指数分布的特征.

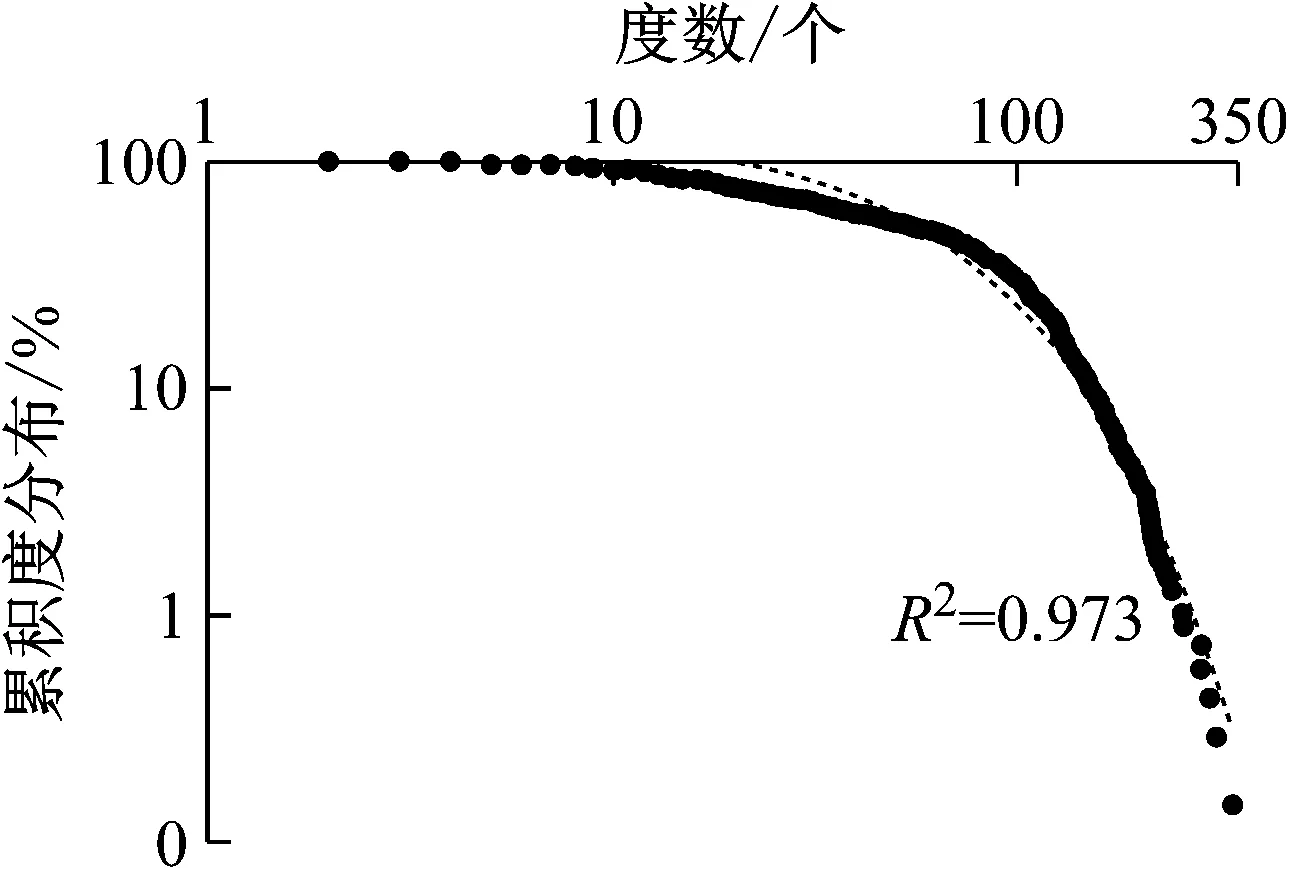
图4 双对数坐标下运输网络节点累积度分布Fig.4 Cumulative degree distribution of HSR transport network under logarithmic coordinates

2.2 聚集系数

聚集系数是描述网络中节点聚集情况的指标参数，是指网络中1个节点相邻的所有其他节点之间的连接情况.某个度为ki的节点i有ki条边将其与其他k个节点相连，这k个节点之间实际存在的边数Ei与其总的可能存在的边数的比值即为节点i的聚集系数.聚集系数越大，说明节点与其相邻节点间的连接紧密度越高.

(3)

式中：Ci为节点i的聚集系数；ki为节点i的度数；Ei为节点i周围k个节点之间实际存在的边数.

对物理网络的聚集系数求解，发现超过90%的车站节点其聚集系数为零，说明大多数车站是两两相邻，较少存在3个车站之间互相连接的情况，整个物理网络全部节点的平均聚集系数为0.030 8，说明当前高铁物理网络密度较低，如果某个节点发生运行中断，列车一般需要绕行才能完成原定计划.图5为高速铁路物理网络聚集系数频率分布图.

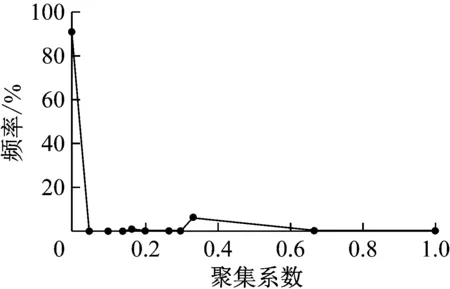
图5 物理网络聚集系数频率分布图Fig.5 Frequency distribution of clustering coefficients in physical network

对运输网络进行聚集系数的求解，其分布情况见图6.与物理网络相比，运输网络的聚集系数明显较高，所有车站节点的聚集系数均在0.26以上，整个网络的平均聚集系数为0.699 9，表现出运输网络的高聚集性质.

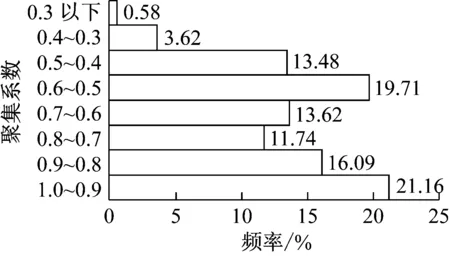
图6 运输网络聚集系数分布情况Fig.6 Frequency distribution of clustering coefficients in transportation network

2.3 平均最短路径长度

在复杂网络中，2个直接相邻的节点间的距离都为1而非其实际地理距离.任意两点间的最短路径长度dij指的是从一个节点i到另外一个节点j所经过的最短距离，即连接这两个节点所需的最少的边的数目.网络的平均最短路径长度是指网络所有N个节点中任意2个节点之间最短路径长度的平均值.其计算公式如下：

(4)

式中：L为整个网络平均最短路径长度；N为网络中的节点个数；dij为节点i和j的最短路径长度.

在物理网络中，2个节点间的最短路径长度所代表的实际含义为旅客从一个车站到另一个车站所需要经过的最少车站个数(即需要通过多少车站的路程)，因此该指标也可以间接反映物理网络的便捷性.

计算得到物理网络的最短路径长度范围为1～91(见图7)，表示在相距最远的2个车站之间旅行需要在途经91个车站，也表示网络半径为45.5.经计算得出物理网络的平均最短路径长度为33.963，即任选网络中的2个车站，平均需要经过约34个车站才能到达目的地；分布较为集中的区域为20～41之间，距离过远的分布较少，最短路径长度超过60的两两节点连接情况占总数的比例低于10%，表明物理网络的便捷性比较良好，旅客的平均出行距离长度并不过长.

在运输网络中，两节点间的最短路径长度所表示的含义为旅客从一个车站乘坐高铁到另一个车站需要乘车的次数，同时旅客乘坐列车的次数等于其需要进行换乘的次数加1，所以运输网络最短路径长度同时也可以表征换乘次数的分布情况.如表1所示，高速铁路运输网络最短路径长度分布在1～6之间，表示全国的高铁旅客最多需要乘坐6趟高铁即可从任一车站前往其他任何车站；超过90%的最短路径长度分布在1～3之间，表示绝大多数乘客最多需要换乘2次即可前往任一目的地；运输网络的网络半径为3，平均值为2.414 0，即旅客一般仅需换乘1次或2次就可以到达目的地车站.较小的网络半径和平均最短路径长度表明高铁运输网络具有良好的连通便捷性.

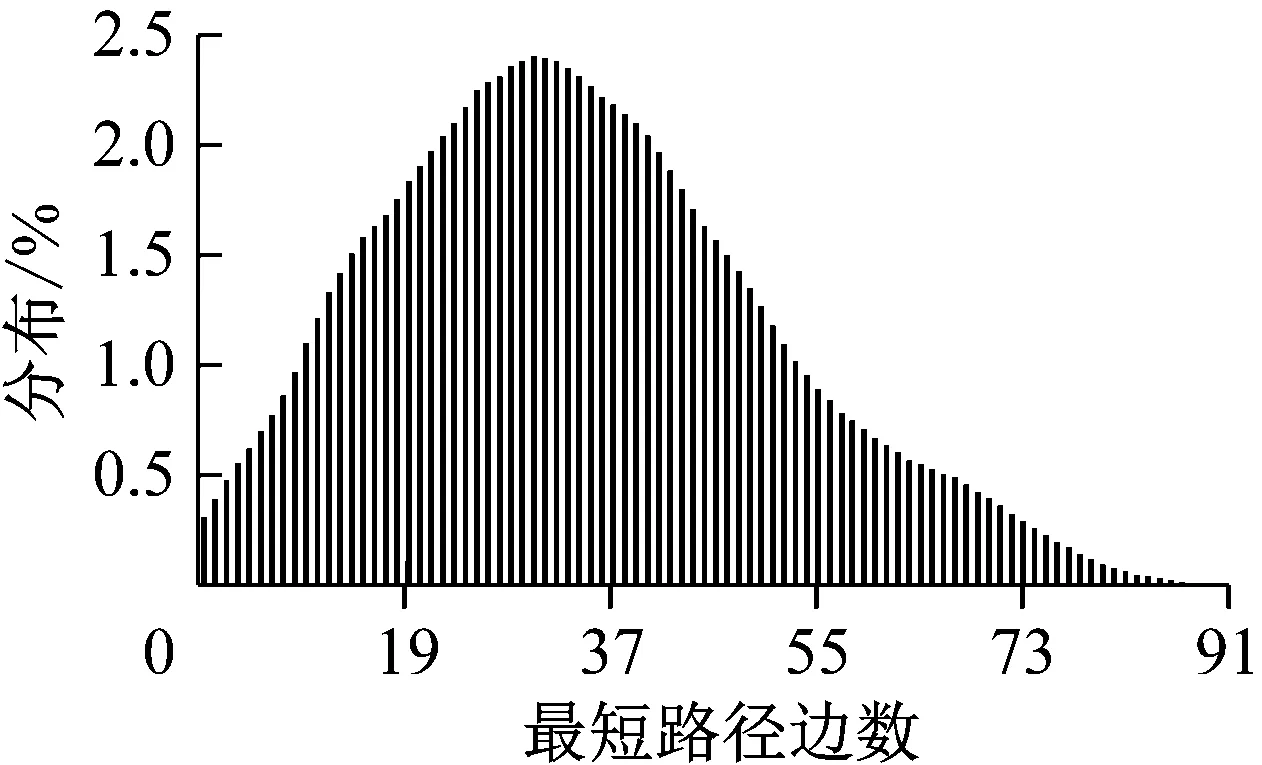
图7 物理网络最短路径长度分布情况Fig.7 Length distribution of shortest paths in physical network

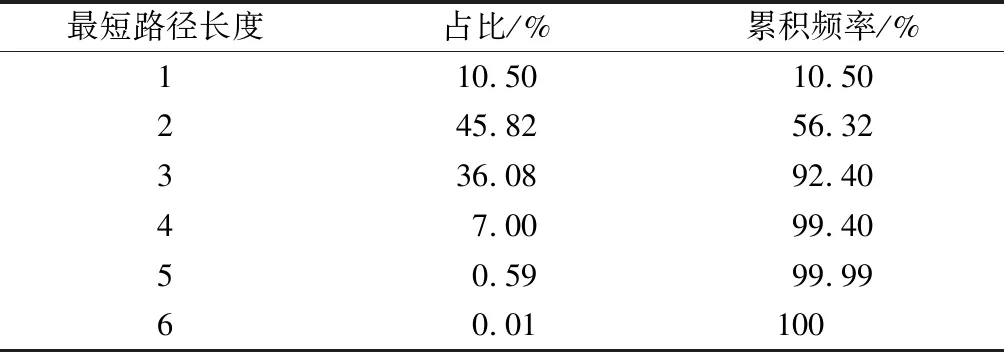
表1 运输网络最短路径长度分布Tab.1 Length distribution of shortest paths in transportation network

2.4 同配性系数

在实际的复杂网络中，度与度之间并不是完全无关的，所以度-度相关性也是复杂网络的重要统计指标.求解度-度相关性可以通过这样的思路：网络中任意1条边均连接2个节点，进而可以得到2个节点的度数，通过遍历所有的边就可以得到2个度数序列，利用皮尔森相关系数(Pearson correlation coefficient)分析这2个序列间的相关性，即为网络的度-度相关性.其皮尔森相关系数r计算公式如下：

(5)

式中：ki、kj分别为边eij节点i、j的度数；E为网络中所有节点间边的集合；M为网络的总边数.

相关系数r描述的是2个变量间线性相关强弱的程度，其取值范围在-1～+1之间.若r>0，表明网络是正相关的，度数大的节点更倾向于连接其他度数大的节点，也称为网络是同配的；若r<0，表明网络是负相关的，度数大的节点更倾向于和度数小的节点相连接，也称为网络是异配的.所以相关系数r也可以称为网络的同配性系数.

对高速铁路物理网络和运输网络进行同配性系数求解，可以得到其同配性系数如下：

计算得到的高铁物理网络和运输网络各自的同配性系数即皮尔森相关系数rp与rt，且均为正数.所以两种网络的度-度相关性都是正相关的，即物理网络与运输网络均为同配网络，网络中度数较大的节点倾向于与其他度数较大的节点相连.这一点与传统认知也相符：一般地，度数较高的高铁客运站绝大多数也是路网中的枢纽换乘站，它们通过线路和开行列车更多地与其他区域的枢纽换乘站相连接.

2.5 高速铁路网络特性小结

表2 4类常见复杂网络模型的特性Tab.2 Characteristics of four general complex network models

根据前面的统计计算，发现我国高速铁路物理网络度分布符合幂律分布特征，且聚集系数较低，同配性系数为正值，是典型的无标度网络.无标度网络也是一种非均匀网络.物理网络中节点的度并没有某个明显的特征值，其平均度数并不能完全代表整个网络，存在少部分度值很高的车站节点，如武汉站、南京南站、郑州东站等，这些车站的存在对网络结构和性能至关重要.而我国高速铁路运输网络的度分布符合指数分布的特征，且聚集系数较大，平均最短路径长度较小，这些复杂网络特性均符合小世界网络的性质特征.表明我国高铁运输网络具有较好的便捷性和连通性.两种网络均为同配网络，新的节点车站一般与既有车站中度较高的车站相连，即新线路一般会连接到既有的枢纽车站，新开通的列车也倾向于停靠既有车次较多的枢纽车站.一般而言，在物理网络中度数排名较高的车站，其在运输网络中的排名也比较靠前，因为连接线路较多的枢纽车站一般也会停靠较多车次的列车.

3 突发事件在高铁网络上的传播动力学研究

传统的传播动力学模型为传染病SI(susceptible infected)以及SIS和SIR模型，这3种模型的适用情况均建立在均匀性假设之上，即都适用于节点分布均匀的均质网络，或者大部分节点度数分布在平均节点度值附近的复杂网络(如ER随机网络).在这种网络中，3种模型内的传播态和易感染态节点密度才可以充分接触.而在现实中，绝大多数网络并不符合这一特点，传播态节点在不同的局部范围内其传播过程并不一致.

3.1 传播模型假设

在现实运营中，列车在车站间的晚点一般是1个车站接着相邻车站进行传播，晚点这一网络上的节点“疾病”随着列车的前进方向扩散，以及受到影响的其他列车前进的不同方向不断地向外扩散传播，这种传播过程对应的节点和车站为高铁网络中的相邻车站及连接车站的线路，即为物理网络范畴下的节点和边，影响到的是相邻车站间的连接状态，而不是侧重于衡量旅客换乘次数因素(即运输网络).所以本节研究的列车晚点传播模型，是基于高速铁路物理网络下的，考虑到的网络特征也是前文计算得到的物理网络相关特征情况.通过前文分析，了解到高速铁路物理网络是典型的无标度网络，也属于异质网络，所以不能直接使用有着均匀性假设的经典模型进行计算.

综合网络性质因素，本文建立晚点传播模型时有以下假设条件：

(1)高速铁路物理网络的度分布具有幂律分布的特征，属于较为典型的无标度网络，度数较高的节点特征不能被平均度数直接取代；

(2)网络中的车站节点状态分为晚点状态和正常状态两种情况，状态变化是一个动态过程，且可以多次往复改变；

(3)晚点状态下的节点，按照其节点度数的不同进行分类，相同度数的节点为一组，将晚点状态下的节点再细分为多个小组，认为不同度数的节点具有并不完全相同的传播情况，而同一小组下的节点传播过程相同或相似；

(4)每前进一个时段，与晚点状态节点相连的正常态节点会以一定概率转变为晚点状态，即被相邻的晚点车站“传染”.

3.2 传播模型的建立

根据模型假设条件，设t时刻度数为k的所有节点中晚点状态节点所占比例为ρk(t)，正常状态节点所占比例为υk(t)；正常节点每时段从正常状态变为晚点状态的概率为λ，从晚点状态恢复为正常状态的概率为μ，则可以得到如下微分方程组：

(6)

式中：υk(t)为t时刻网络度数为k的节点中正常节点所占比例；ρk(t)为t时刻网络度数为k的节点中晚点节点所占比例；λ为晚点节点的传播效率；μ为节点恢复效率；k为节点度数；θ(ρk(t))为度数为k的节点与晚点状态节点相连接的概率.

方程中，一个未被“传染”的正常状态度数为k的节点与kθ(ρk(t))数量的晚点节点相连，则所有度数为k正常节点每时段转变为晚点节点的数量为λkυk(t)θ(ρk(t)).该模型以SIS模型为基础，考虑到不同度数节点之间的连接情况而引入变量θ(ρk(t))，表示度数为k的节点与晚点节点相连的概率，即度数为k的节点其邻近的k个相连节点中晚点节点所占比例，所以有

(7)

式中：P(k)为网络中任一节点其度数为k的概率；P(k′|k)为度数为k的节点与度数为k′节点之间相连的概率.

参数λ为晚点传播效率，是指网络中某个节点发生突发事件造成列车晚点后，在每一单位时段内，造成周围相连车站节点也随之发生列车晚点的概率大小；μ为晚点车站恢复正常状态的概率，某站发生列车晚点的情况后，如果经过合理的调度运行调整与客运组织协调，当列车恢复正点运行时可以认为其已从晚点状态转变为正常状态.可以通过以往的相关运输组织经验对其进行测算，统计发生各类突发事件后一段时间内某个车站节点与相邻其他节点间发生列车晚点及晚点车站的恢复情况，与正常情况下开行计划列车数进行对比.其公式为

λ=Nl/Np

(8)

μ=Nr/Np

(9)

式中：Np为车站与相邻站间未能按时运行的晚点列车数量；Nr为车站与相邻站间从晚点状态恢复正点运行的列车数量；Np为图定计划中全部列车数量.

3.3 模拟结果分析

3.3.1不同有效传播率

首先分析传播效率和恢复效率对传播范围的影响作用.因P(k=2)在各节点度数中最大，各单条线路中上下行两端各连接1个相邻车站的非换乘站最为普遍，所以在研究有效传播率对传播过程的影响时，可以先假设突发事件导致的列车晚点情况发生在度数为2的高铁客运站，将其作为典型案例进行实验分析.给定不同的传播效率和恢复效率，通过计算得到相应的列车晚点传播范围随时间变化的实验结果.

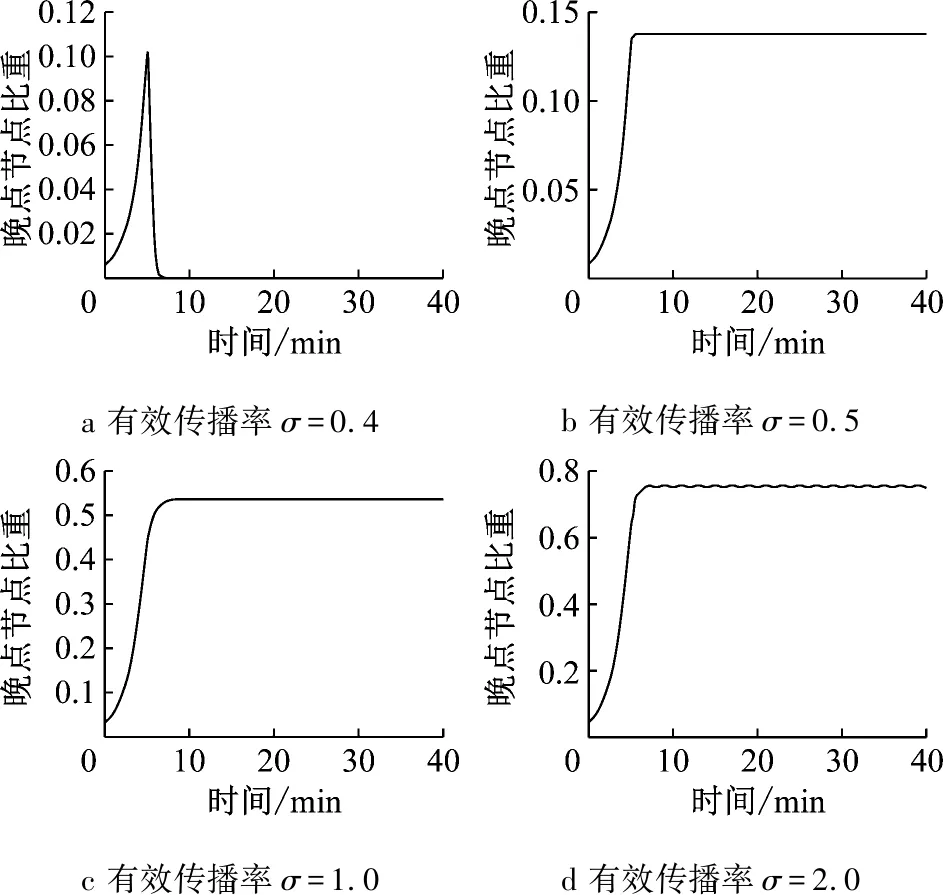
以度数k=2的车站为例，分别将晚点传播模型相关参数取值为：λ=0.3,μ=0.75；λ=0.3,μ=0.60；λ=0.3,μ=0.30；λ=0.3,μ=0.15.经计算得到其各自的传播影响范围，如图8所示.

a 有效传播率σ=0.4b 有效传播率σ=0.5c 有效传播率σ=1.0d 有效传播率σ=2.0

由图8可以得到以下信息：

(1)不同传播效率和恢复效率(即不同的有效传播率)对传播影响范围有着直接影响.传播过程总体类似，可分为两个阶段：前期增长阶段和后期阶段.晚点节点比重从初始状态开始快速增加，随后达到顶峰，其有效传播率越高，峰值晚点节点也越多.

(2)晚点影响的持续存在传播阈值.当模型的有效传播率σ为0.4时，后期为消散阶段，车站节点受到影响而晚点的车站在经过最高峰值后会迅速恢复为正常状态，最终整个高铁网络中不存在列车晚点的节点车站；而当其有效传播率较大时后期为稳态阶段，网络中始终存在晚点车站，传播范围大致保持稳定不变，其稳态时的晚点节点比重维持在峰值附近，晚点状态节点与正常状态节点之间保持平衡.

3.3.2不同初始状态

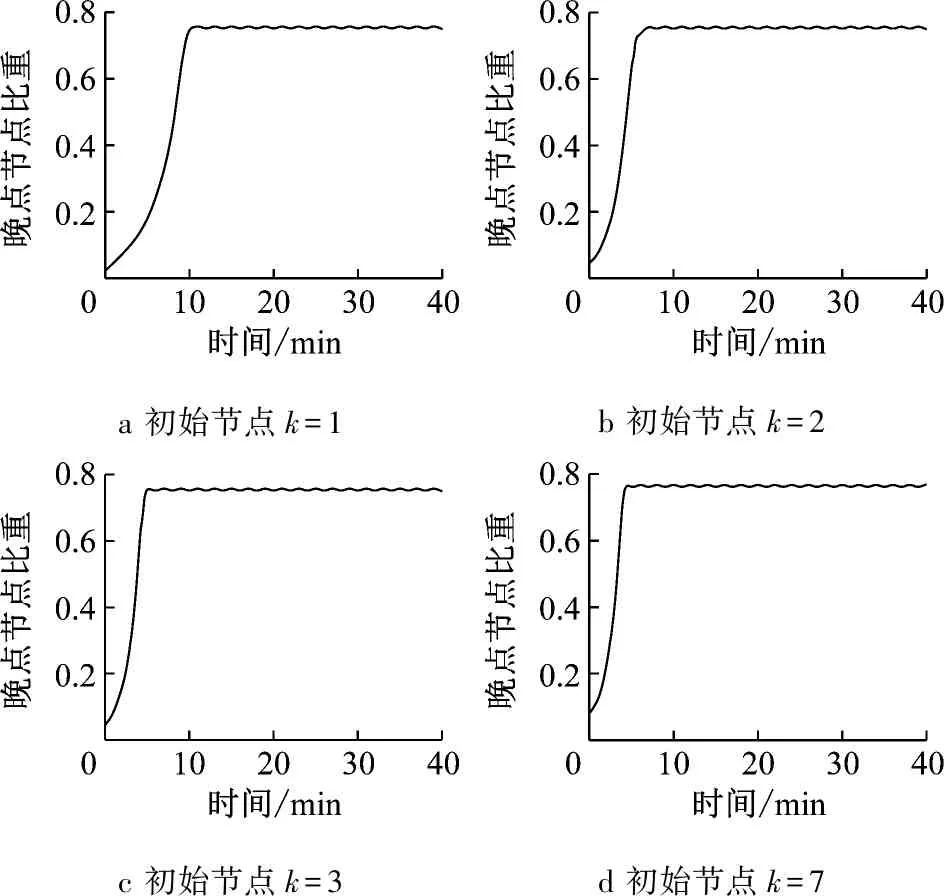
分析不同状态对传播过程的影响.这里的初始状态是指列车晚点发生地的不同车站类型.其初始晚点节点分别选择度数为1的首发终到站、度数为2的中间车站、以及度数为3及以上的换乘车站等几类不同车站.

以度数k分别为1、2、3、7为例，其中有效传播率均取σ=2.0.图9表示当初始晚点节点为该站时的传播扩散过程.

a 初始节点k=1b 初始节点k=2c 初始节点k=3d 初始节点k=7

从图9可以看出：

(1)初始节点的度数对晚点传播扩散过程中的前期增长阶段有一定影响.发生列车晚点的初始车站其节点度数越大，传播扩散也越快，即晚点发生在多条线路交汇的枢纽车站时，其传播会比发生在首末站和中间车站时扩散得更快.

(2)初始状态对传播扩散过程中的后期稳态阶段影响不大.不同初始条件在进入稳态阶段后的列车晚点节点比重大致相同，不管晚点发生在度数较高的初始节点还是度数较低的初始节点，受其传播影响的节点数量峰值基本没有差别，稳态时的影响范围仍主要取决于传播效率与恢复效率.

(3)将结论带入现实运营条件中进行解释.当连接多个方向的枢纽车站发生突发事件后，极有可能在短时间内使得多个方向的相邻车站列车都不能正点到发，所以其前期的传播速度很快；而如果发生晚点的车站为始发站，则其在传播开始阶段仅能影响到单条线路方向上的相邻车站，所以传播速度相对较慢，但因其所在线路与整个网络连通，列车晚点终究会传播到度数较高的枢纽车站，再由枢纽车站继续传播到其他车站，所以长时间后的稳态范围与前种初始状态条件下的最终传播范围基本相同.

3.4 控制列车晚点在网络中传播扩散的相关措施

可以看到，列车晚点在高速铁路网络中的传播扩散基本可以分为两个阶段：前期增长阶段与后期稳态阶段(或消散阶段).前一个阶段的节点变化情况主要受到传播效率、恢复效率以及初始晚点节点状态条件的影响，后一阶段的节点变化主要取决于有效传播率.所以为防止突发事件下全路网发生大面积的列车晚点，进而对整个路网的性能、旅客服务都造成重大危害，就需要针对这些相关影响采取如下相应控制措施：

(1)减缓列车晚点的传播扩散效率.如果能将有效传播率降低至0.5左右时，即保持晚点车站相邻的其他车站中至少一半保持正常状态，则传播范围会出现明显减小.一般可采取的调整措施主要有加速车站作业、组织旅客快速乘降、压缩停站时间、压缩区间运行时间等.

(2)增加枢纽换乘车站的应急防御措施.如果突发事件发生在连接线路较多的枢纽换乘车站，其传播扩散到相邻车站的速度就更快.应在这些度数较高的枢纽换乘站提前做好应急防护，定期安排演练，提高车站各项作业的效率，避免突发事件发生时延误更多时间；在发生突发事件后，也应先对这些车站进行重点监控和及时处理，避免其晚点迅速扩散至多条线路方向上的相邻车站.

(3)当单条线路上某个非换乘站发生晚点时，应尽量在列车晚点传播扩散至枢纽换乘站之前就恢复正点运行，避免列车晚点影响到换乘车站的到发线使用及车站运输组织，防止晚点从单条线路经换乘站扩散至其他线路车站上，缩小其传播扩散范围.

(4)在紧急情况下，为避免部分车站出现的列车晚点扩散至更多地区，可以先将部分晚点的车站节点从整个网络中剥离，隔断其与其他正常状态的车站节点之间的联系，保证其他地区的列车能够不受影响正点到发，然后再将晚点车站的列车按照列车等级恢复运行.

4 结论

(1)根据我国高速铁路线路开通情况及列车运行图，构建高速铁路物理网络和运输网络两个网络拓扑结构模型，并运用复杂网络理论分别进行定量相关特性指标的统计与计算，并根据这些指标的计算结果总结我国高速铁路网络的网络特性，得出物理网络符合无标度网络性质，网络中存在少部分度值很高的车站节点，如武汉站、南京南站、郑州东站等，它们的存在对网络结构和性能至关重要；而运输网络符合小世界网络的性质特征，表明我国高铁运输网络具有较好的便捷性和连通性，旅客一般不需换乘或仅需换乘一两次就可以很方便地抵达网络中的任意目的地.

(2)结合高速铁路网络自身的无标度、非均质等网络特性，建立高速铁路列车晚点传播模型，研究晚点在网络上的传播扩散过程.通过对不同传播效率、不同初始晚点车站等情况进行研究对比，得出列车晚点在网络上的传播过程一般可以划分为前期增长阶段和后期稳态阶段(或消散阶段)两个阶段，在网络拓扑结构给定的前提下，前期传播扩散主要受到传播效率、恢复效率和初始晚点车站条件的影响，后期进入稳态时的晚点节点数量主要受到有效传播率的影响.提出控制和减缓列车晚点在网络中扩散蔓延的相关措施.

(3)高速铁路网络的复杂特性及传播规律研究，可以应用于未来新线的建设以及运行图调整优化中.高速铁路物理网络的可靠性提高一般在规划设计阶段就需要进行考虑，如在车站选址时要注意关键车站尽量避免设在容易发生自然灾害的区域位置，同一枢纽内新建高速铁路客运站时可以考虑设计联络线与既有站相连；而运输网络的特性能够作为判别当前运行图好坏的一种指标，运输网络的平均最短路径反映旅客出行的便捷性，路径分布越大，则表明当前运输条件下旅客需要的换乘次数越多，出行越不便.