利用蒙特卡洛方法评估多个勘探圈闭的策略

赵 华 王 斌 陈家杰 皇甫煊 张 伟 路云英

（中国石化集团国际石油勘探开发有限公司）

0 引言

石油资源国会对其具有潜力和风险的勘探区块通过公开招标的方式吸引国际石油公司进行投资[1-2]。近年来，国内石油公司也逐渐开展“走出去”战略积极拓展海外油气勘探业务。对于石油公司来说，如何合理确定投标的报价就成为能否得到该勘探机遇的关键[3-5]。

本文从两个方面详细讲述了如何确定报价的基本内容[6]：第一是如何确定成功概率和资源量规模的大小；第二是如何确定该资源量规模带来的经济价值，该价值是确定项目报价的主要依据。首先，在对多个圈闭进行资源量评估过程中，采用蒙特卡洛方法对以下两个评价指标进行测算：①至少成功发现一个商业油气藏的概率；②含风险概率资源量规模。其次，商业化的油气勘探行为离不开对经济价值的评估，在确定了成功概率和含风险概率资源量规模之后，需要进一步考虑资源量规模和资源量价值之间的关系。期望价值EMV是评估资源量价值的重要指标，它是钻探失败价值和成功价值的综合体现，是全面定量分析最终资源量价值的有效工具。然而，EMV的最大化并不是最终决策的方向，在利用蒙特卡洛方法建立EMV评估模型的过程中，需要分析各成功概率的相关性、钻井顺序和钻井数量等3个方面对含风险概率资源量、成功概率、经济成功概率及EMV的影响，从而做出最终的投资决策。传统的风险评估常用到决策树方法，相比于蒙特卡洛方法，决策树方法存在一定的不足[7-9]：决策树方法是由不同的分支和节点组成，若需计算多个圈闭的成功概率，必须首先熟知各圈闭之间包含的复杂计算逻辑；决策树方法在成功概率间相关性的处理上较为复杂，尤其当圈闭数量较多时（10个以上），计算就更加复杂；决策树既不能精准计算经济极限概率，也不能得到净现值NPV（Net Present Value）的累计概率分布，从而也不能得到P10、P50、P90净现值，而只能得到一个平均值即EMV的价值。因此，本文采用蒙特卡洛方法对多个圈闭的勘探风险进行评估。

1 多个圈闭的含风险概率资源量评估

1.1 评估单个圈闭的地质成功概率和资源量概率分布

1.1.1 单个圈闭地质成功概率

单个勘探圈闭地质成功概率的评估须全面考虑5个重要的成藏基本条件[10]：①烃源岩条件；②储层条件；③盖层条件；④构造圈闭条件；⑤油气运移条件。这5个关键条件的成功概率须通过专业的技术团队在众多资料中加以细致分析和经验判断，并采用定量的数值表征出来[11]。它们的取值范围是0～100%，数值越高，代表成功概率越高。例如：对于某圈闭Z，每一个成藏条件的成功概率如表1所示，储层成功概率是70%，代表有70%的概率该圈闭具备储层条件，30%的概率认为该储层不发育。总的地质成功概率为5个成藏条件成功概率的乘积，圈闭Z总的地质成功概率为29%，即该单个圈闭成功发现的概率为29%。

表1 Z圈闭地质成藏成功概率Table 1 Geological success probability of hydrocarbon accumulation in Z Trap

1.1.2 单个圈闭的资源量概率分布(P10/P50/P90)

单个圈闭的最终可采量可采用容积法计算[12]， 其公式为：

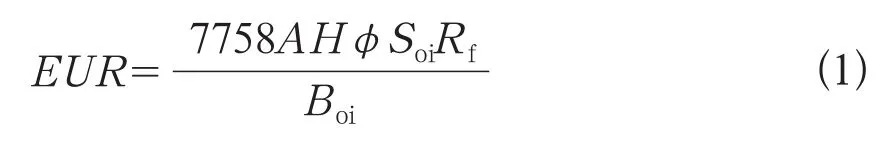
式中EUR——最终可采量，bbl；

A——含油面积，acre；

H——有效厚度，ft；

φ——有效孔隙度，%；

Soi——原始含油饱和度，%；

Rf——采收率，%；

Boi——原油体积系数。

通过地质油藏技术团队的综合分析，对计算过程中关键变量A、H、φ、Soi、Rf、Boi等给定合理的变化范围[13-14]。表2是各关键变量取值及其分布形态，每个参数的分布形态需要结合样本实际情况而选择。

确定以上参数后，通过数万次甚至上百万次的随机变量的抽取和运算，最终得出可采量的累积概率分布曲线，从而得到该圈闭资源量的P10/P50/P90以及平均值（图1），一般选取平均值作为该圈闭最可能获得的资源量规模，即该圈闭资源量为286×106bbl。资源量概率分布的另一种分布形式是频率分布，它是各资源量规模区间范围内发生的频率，在随机模拟结果中代表每个不同资源量规模区间内发生的次数，它呈对数正态分布的形态（图1红线）；把频率分布累积求和就得到了累积概率分布曲线（图1蓝线）。

表2 资源量计算中关键变量的取值和分布情况Table 2 Value and distribution of key variants in the calculation of resource extent

图1 圈闭资源量累积概率分布和频率分布图Fig.1 Cumulative probability distribution and frequency distribution of trap resources

1.2 评估多个圈闭的成功概率和风险概率资源量

1.2.1 多个圈闭的蒙特卡洛参数输入

各圈闭的成功概率、资源量规模及分布确定之后(表2)，输入各圈闭的分布形态和规模[15]。如：有A、B、C 3个圈闭，且3个圈闭各自独立，它们各自的成功概率和资源量规模的分布情况如表3所示。对成功概率的分布形态进行逻辑判断，即“是—否”分布。例如：A圈闭的油气运移成功概率为60%，输入“1”对应60%的成功概率，“0”对应40%的成功概率。其他成功概率的输入依次类推。单个圈闭的资源量分布，按照每个圈闭实际模拟形态和规模进行输入。

1.2.2 至少发现一个圈闭的成功概率

COS（chance of at least one success）代表至少发现一个圈闭的成功概率[16]。COF（chance of failure）代表所有圈闭全部失败的概率，它的数值等于1-COS。本例中假设以上A、B、C 3个圈闭全部钻探，那么：

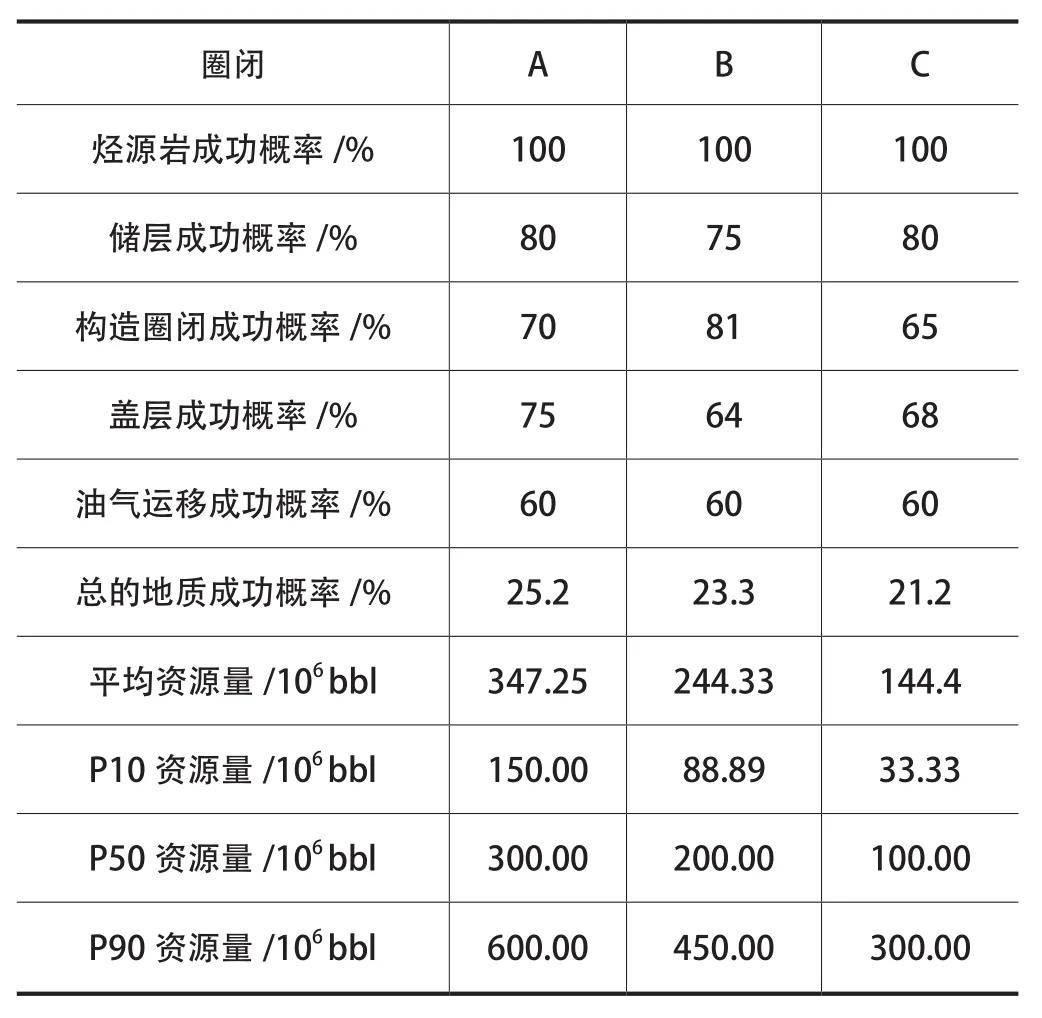
表3 多个圈闭的成功概率和资源量输入参数Table 3 Input success probability and resource extent of multiple traps

（1）至少有一个圈闭成功的概率是多少？全部失败的概率是多少？

（2）用PA、PB、PC代表单个圈闭成功发现的概率，PAB、PBC、PAC代表其中两个圈闭成功发现的概率，PABC代表3个圈闭都成功发现的概率。那么，PA、PB、PC、PAB、PBC、PAC、PABC各是多少？

利用蒙特卡洛工具，给定逻辑判定，最终模拟得到的结果如表4所示，7种情况的成功概率求和等于COS即54.8%，COF等于1-COS=45.2%。

表4 蒙特卡洛方法成功概率和COS、COF结果Table 4 Success probability of Monte Carlo method, COS and COF results

1.2.3 含风险概率资源量

在风险勘探阶段，如果有多个潜在的有利圈闭可供抉择，人们往往最关心的另外一项评价指标就是考虑各种风险因素后能够获得的资源量规模，即含风险概率资源量，它是各圈闭资源量规模与总的地质成功概率的乘积。对于多个圈闭的含风险概率资源量，则等于单个圈闭的含风险概率资源量的总和。

与此同时，不含风险概率资源量代表在不考虑失败概率情况下的资源量，它同样也是一个资源量的概率分布，其值等于风险概率资源量除以COS。

利用蒙特卡洛随机模拟（10万次以上），得到了资源量累积概率分布曲线（图2），由图2可知：

（1）含风险概率资源量在累积概率小于45.2%范围内均为零，3个圈闭全部钻探的情况下，最终得到的含风险概率资源量为175×106bbl。

（2）如不考虑失败风险，则得到不含风险概率资源量分布，整个曲线形态呈“S”形，在3个圈闭全部钻探且至少成功发现一个圈闭的情形下，能够获得的资源量规模为320×106bbl。

图2 含风险概率资源量和不含风险概率资源量的分布规律Fig.2 Distribution laws of resource extents with and without risk probability

综合以上可以得出：含风险概率资源量的真正涵义就在于它综合考虑了圈闭的成功概率和资源量规模，能够为决策者揭示在考虑失败风险的前提下可以获得的资源量规模及其概率分布。而不含风险概率资源量，可以用来表征在无失败风险的情形下能够获得多大的资源量规模。

1.2.4 成功发现圈闭的平均数量

发现圈闭的平均数量也是一个重要的评估指标，它从侧面给决策者提供潜在信息即发现圈闭个数的概率。通过随机模拟的方式对A、B、C 3个圈闭的总的地质成功概率求和后除以COS，即可得出平均圈闭数量为1.3，即能够平均成功发现1.3个圈闭。那么，成功发现1.3个圈闭如何理解？它的深层含义是什么？

图3展示了发现1个、2个、3个圈闭的频率分布曲线及资源量规模累积概率分布曲线，可以看出：

（1）对于P10的资源量规模只可能发现1个圈闭（全部落在橘色区域），即成功发现圈闭的平均数量为1。

（2）P50的资源量规模可能发现1个圈闭，也可能发现2个圈闭（蓝色区域和橘色区域，蓝色区域大约占20%），成功发现圈闭的平均数量为1.2。

（3）P90的资源量规模可能发现1个圈闭、2个圈闭、3个圈闭（蓝色区域、橘色区域和红色区域），成功发现圈闭的平均数量为1.9。

（4）平均值的资源量规模可能发现1个圈闭，也可能发现2个圈闭（蓝色区域和橘色区域，蓝色区域大约占30%），即成功发现圈闭的平均数量为1.3，发现2个圈闭的概率要比P50的概率高。

图3 多个圈闭的不含风险概率资源量分布（油气运移成功概率完全不相关）Fig.3 Distribution of resource extents without risk probability of multiple traps(the success probability of hydrocarbon migration is fully independent)

通过以上分析，成功发现圈闭的平均数量将给决策者提供如下潜在信息：在P50或者平均值的资源量规模下，成功发现圈闭个数的可能性，尤其是当面临多个圈闭选择的时候，可以指导人们最可能发现圈闭的个数。

对比A、B、C 3个圈闭初始的成功概率和COS，A、B、C 3个圈闭各自独立的地质成功概率分别为25.2%、23.3%、21.2%，而将这3个圈闭同时钻探时，COS会增加至54.8%，这说明对多个圈闭进行风险评估时，单个圈闭的初始成功概率要低于COS（图4）。A、B、C 3个圈闭各自的资源量分别为347.2×106bbl、244.3×106bbl、144.4×106bbl，而至少能够发现一个圈闭的资源量介于最大和最小的资源量规模之间。

图4 A、B、C 3个圈闭分别评估和综合评估的结果对比Fig.4 Comparison between individual assessment result and comprehensive assessment result of A,B and C trap

1.3 相关性对成功概率和风险概率资源量的影响[17]

以上所述结论的前提是A、B、C 3个圈闭各自独立，相互之间不存在相关性。但实际情况中，圈闭往往具有某些相同的地质成藏条件，这就需要技术团队通过分析判断，给定某个或者某几个成功概率的相关性，这势必会影响最终的概率分析结果。在相关性设置中，1代表完全相关，0代表完全不相关。对于完全相关，就是如果A成功B一定成功。对于完全不相关，则是相互独立。本例中假定：A、B、C 3个圈闭的某一个成功概率——油气运移成功概率（下文中完全相关或完全不相关的情形均指油气运移成功概率完全相关或完全不相关）具有相关性，且相关系数为1（完全相关），即：当A圈闭具备油气运移条件的时候，B和C圈闭也一定具备油气运移条件，反之亦然（在蒙特卡洛中设定，A的油气运移成功概率与B相关，B的油气运移成功概率与C相关）。

通过对比完全不相关和完全相关的情形（表5、图5），可以得到：

（1）7种情况的概率都发生了不同程度的变化，COS从54.8%降到了46.2%，COF由45.2%增加至53.8%，即相关性的增加，降低了COS。这是由于相关性的增加，大大增加了COF的概率，最终导致COS降低。

（2）在完全不相关和完全相关的情形下，虽然后者不含风险概率资源量较高（图5），但两者的含风险概率资源量是一致的，都等于175×106bbl。也就是说，虽然相关性的增加降低了COS，但对含风险概率资源量不影响。对投资者来说，寻找相关性非常高并且单个圈闭的成功概率也较高的圈闭，将会更容易获得成功。

表5 不同相关性下的成功概率及COS, COF的对比Table 5 Success probability at different dependencies, COS and COF comparison

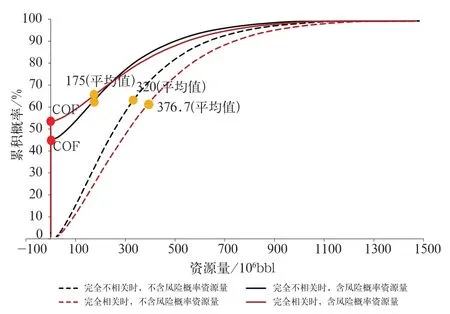
图5 不同相关性下的含风险概率资源量和不含风险概率资源量对比Fig.5 Comparison between the resource extent with risk probability and that without risk probability at different dependencies

（3）随着相关性增加，成功发现圈闭的个数也会相应增加。图3是在油气运移成功概率完全相关的情形下发现1个、2个、3个圈闭的频率分布曲线及不含风险概率资源量累积概率分布曲线。相比较完全不相关的情形，完全相关情形下成功发现圈闭的平均数量由1.3增至1.5，各个级别的资源量规模增加了成功发现2个圈闭的可能性（图6）。这很好地解释了随着相关性增加，成功发现圈闭的平均数量也会相应增加。

完全相关和完全不相关的情形是相关性的两个极端，大多数情况下，成功概率之间可能会存在部分相关的情形，例如给定油气运移成功概率的相关系数为0.6，那么它的COS和含风险概率资源量平均值又会是怎样的？与前面两种极端的现象对比会有怎样的趋势？通过计算（图7）不难发现：

图6 多个圈闭的不含风险概率资源量分布（完全相关）Fig.6 Distribution of resource extents without risk probability of multiple traps(fully dependent)

（1）对于COS，随着相关性的增强而降低。

（2）对于含风险概率资源量平均值，无论相关性如何变化，最终得到的含风险概率资源量平均值都是一致的。

（3）对于不含风险概率资源量平均值，随着相关性的增强，其值逐渐升高。

图7 不同相关性下的COS和资源量对比Fig.7 Comparison between COS and resource extent at different dependencies

2 评估多个有利圈闭的期望价值EMV

2.1 建立EMV评估模型

2.1.1 建立NPV与资源量的关系对应曲线

通过蒙特卡洛随机模拟，得到了多个圈闭含风险概率资源量规模，下一步需要对其进行价值评估，即EMV评估。那么，资源量规模和价值之间有没有一一对应的关系？发现不同个数的圈闭对价值又有何影响？一般来说，考虑到地面投资，在相同资源量规模下，钻遇到多个圈闭会带来额外的地面投资，因此，多个圈闭情形下，最低开发资源量规模要高于钻探1个圈闭的情形。所以在计算EMV之前，首先要确定不同圈闭个数情形下资源量规模与NPV的关系曲线，找到这3种不同情形下的经济极限资源量。也就是说，对于成功发现1个、2个、3个圈闭的情形，分别按照图8中对应的关系曲线计算NPV，对于未达到最低开发资源量规模的情形，它的价值将等于相应的钻井失败的价值（图8）。

图8 不同圈闭个数下资源量与NPV关系曲线Fig.8 Relationship between resource extent and NPV for different amounts of traps

需要说明的是，利用这种建立NPV与资源量规模的关系曲线得到NPV的方式是一种非常直接和高效的方式。它把经济模型中复杂的财税计算逻辑关系精简为资源量与NPV的单一关系曲线，从而提高了蒙特卡洛方法中百万级抽样次数的运算速度。而建立这种关系曲线的核心就在于：①选择几个具有代表性的（比如3～5个）单个圈闭的资源量值；②设计并规划好开发相应规模资源量的地面工程、井数及投资成本方案；③将该方案放入经济模型中计算NPV；④利用资源量和对应的NPV数据点采用回归方式拟合关系曲线。当NPV=0时，对应的资源量阈值就是经济极限资源量。同样的方式也可以得到成功发现2个圈闭甚至3个圈闭的经济极限资源量（图8）。

2.1.2 钻探失败情形的价值预估

钻探失败的情形分为两种：一种是1个圈闭都没发现，比如，钻3个圈闭全部都失败；另一种是有发现但不具有商业开发价值[18]。对于这两种情形，都采用钻井成本作为其损失价值，因为一般会选择损失钻井和获取资料的费用，而不会冒着更大风险的去投入开发。本文中，假设每口井的钻完井成本为1亿美元，不考虑其他附加损失。

2.1.3 EMV的输出结果

利用以上输入参数，构建期望价值评估模型，利用蒙特卡洛随机模拟，最终可得到NPV累积概率分布图。图9中所示是按照A—B—C顺序实施情形下的NPV累积概率分布曲线，通过分析可以得知：

（1）当不考虑最小开发规模时，COS是54.8%，COF是45.2%（表4）。在考虑了经济极限资源量后，定义为经济成功概率，相应的失败概率定义为经济失败概率。图9中失败概率由45.2%提高至60%，原因在于经济极限资源量的限定增加了失败的可能性。

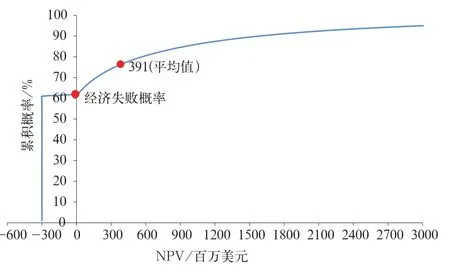
图9 NPV 累积概率分布曲线（完全不相关）Fig.9 Distribution of NPV cumulative probability(fully independent)

（2）NPV的平均值为3.91亿美元，它就是最终得到的EMV。图9中NPV曲线代表的是整个项目层面，具体到不同的合同利益方要乘以相应的工作权益。

2.2 关键因素对期望价值的影响

2.2.1 钻井数量及成功概率相关性

2.2.1.1 钻井数量

石油公司决策投标时，为了获得最大收益并增加中标可能性，会尽可能多地承诺最低工作量，如本例中，目标区有3个圈闭，石油公司的做法通常是分别评价对比承诺3口井、2口井和1口井的钻井方案（图10至图12），从而决定投标时的最低工作量。

（1）钻3口井。如果承诺钻3口井，则无论前一口井钻探结果如何，3口井都必须钻（图10）。

（2）钻2口井。如果承诺钻2口井，第三口井可根据前两口井的钻井结果决定是否继续钻探，一般前两口井都失败时，第三口井放弃钻探（图11)。

（3）钻1口井。如果只承诺钻1口井，一般第一口井钻探成功，后续两口井都钻探；第一口井钻探失败，就放弃后续井的钻探（图12）。

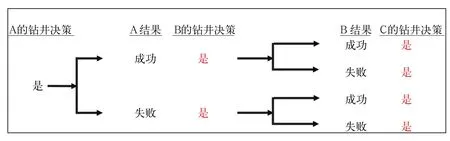
图10 钻3口井的决策Fig.10 Decision of drilling 3 wells

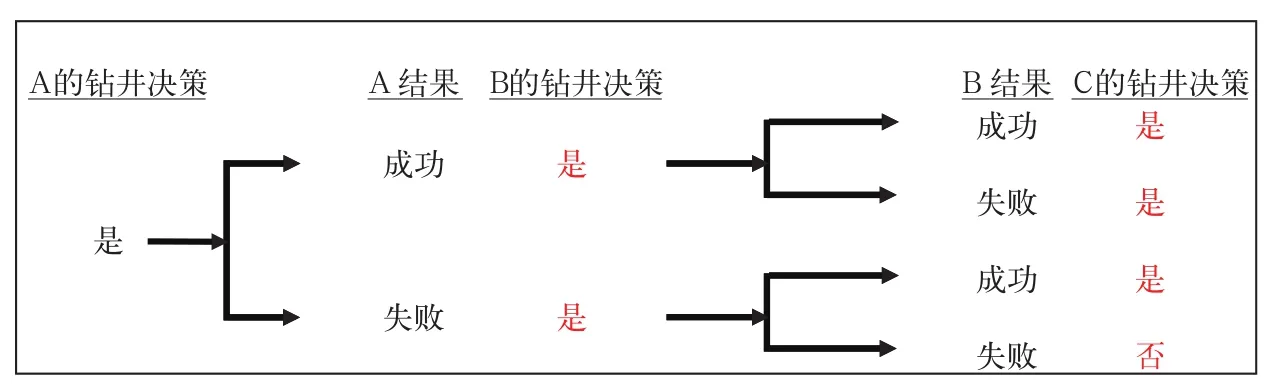
图11 钻2口井的决策Fig.11 Decision of drilling 2 wells

图12 钻1口井的决策Fig.12 Decision of drilling 1 well

2.2.1.2 成功概率相关性

2.2.1.2.1 完全不相关

假设A、B、C 3个圈闭各自独立，钻井顺序为A—B—C，对比3种钻井方案的结果，可以看出(表6、图13、图14）：

（1）在成功概率完全不相关的情形下，随着钻井数量的增加，COS逐渐增加，相应的含风险概率资源量也会增加。

（2）随着钻井数量的增加，期望价值并没有明显规律，反而钻2口井的情形要比钻3口井的情形好，这是由于钻井失败情形损失的价值太高或C圈闭资源量规模太小产生的经济价值太低而不足以弥补开发投资所导致。因此，作为决策者，在投标时选择合适的钻井数量，对项目经济价值的实现至关重要。

（3）蒙特卡洛方法利用随机模拟的优势，分别计算了不同钻井方案下的失败概率及价值。如，承诺钻2口井的情形下，大约6%的概率NPV为-3亿美元，剩余大约56%的概率NPV是-2亿美元。这表示有6%的概率是钻3口井但没有达到经济资源量规模而产生3亿美元的钻井损失，56%的概率是钻2口井失败发生的2亿美元钻井损失。

2.2.1.2.2 完全相关

如果A、B、C 3个圈闭中成功概率完全相关（表6），钻井顺序为A—B—C，对比3种钻井方案的结果，不难发现（表6、图15、图16）：

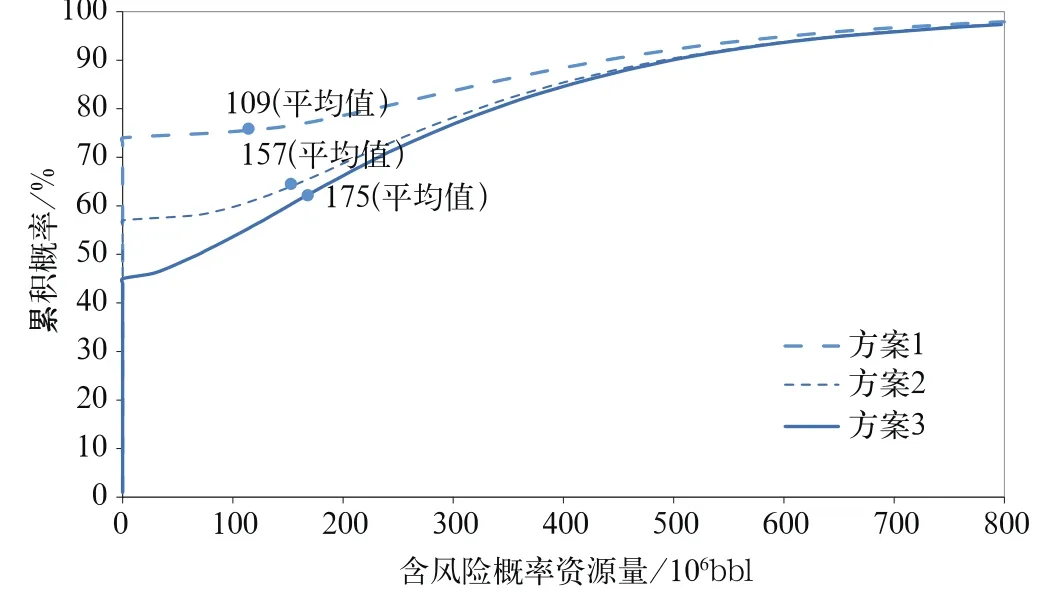
图13 钻井数量对含风险概率资源量的影响（完全不相关）Fig.13 Effect of well quantity on the resource extent with risk probability(fully independent)

图14 钻井数量对NPV的影响（完全不相关）Fig.14 Effect of well quantity on NPV(fully independent)

表6 不同方案的对比Table 6 Comparison between different schemes

图15 钻井数量对含风险概率资源量的影响(完全相关)Fig.15 Effect of well quantity on the resource extent with risk probability(fully dependent)

（1）成功概率完全相关的情形下，随着钻井数量的增加，COS、含风险概率资源量、期望价值的变化规律与完全不相关情形时完全一致。

（2）随着相关性增大，经济成功概率降低，不含风险概率资源量和期望价值增大，这意味着相关性的增大使可能获得的资源量价值相应的增大，从而也说明寻找相关性及成功概率均较高的圈闭会更容易获得重大发现和收益。

2.2.2 钻井顺序

如果A、B、C 3个圈闭各自独立，改变钻井的顺序为B—A—C，同样对比3种钻井方案的结果，不难发现（表6）：

（1）改变钻井顺序后，在钻1口井的情形下，COS和含风险概率资源量及期望价值都大大降低。这是由于B圈闭的资源量规模和成功概率均小于A圈闭。

（2）在钻2口井和3口井的情形下，虽然改变了钻井顺序，但COS和含风险概率资源量都不会发生变化，从而期望价值也不会发生变化。

由此可见，在选择钻井顺序时，应综合考虑成功概率和资源量规模的大小，即需要考虑两者乘积的大小。选择一个中等资源量规模但成功概率较高的圈闭进行钻探会比选择一个资源量规模很大但成功概率却很小的圈闭能获得更高的期望价值。

3 多个勘探圈闭的投标策略

期望价值是成功价值和失败价值的综合体现，通过以上对比分析（表6），总结得出最终策略如下[19-20]：

（1）增加钻井数量，虽然可以增加成功概率，但并非钻井数量越多越好，需考虑其对经济价值的影响，通过优化得到最佳钻井数量。如本例中，钻2口井的价值比3口井更优。

（2）在相同钻井数量情形下，改变钻井顺序，可能会获得不同的价值。当各圈闭资源量规模和成功概率的趋势不完全一致时，需综合考虑两者乘积的大小决定钻井顺序。

（3）相关性的增大，可增大期望价值。因此，钻井前需寻找圈闭之间的相关性，以尽量增大可能获得的价值。

（4）期望价值是成功价值和失败价值的叠加效果，在最终决策点的选择上，不能一味寻求期望价值的最大化而忽略了成功概率及失败价值的承受能力的影响。当期望价值最高，但成功概率较小且失败价值在石油公司现有的现金流状况下不能完全承受的条件下，应选择较低的期望价值但失败价值可承受的方案。

（5）在勘探投标环节中最重要的是竞标签字费和钻井数量。签字费标准可参考评估的期望价值，作业者和政府承诺的签字费一般不会高于期望价值。人们既不想通过过高的溢价方式中标，也不想报价太低而错失勘探机遇，所以合理评估项目期望价值是我们中标的关键。

4 结论

鉴于蒙特卡洛方法具有全面和独特的优势，本文创造性地构建了一套较完善的风险评估工具，并通过具体的项目实例详细阐述了运用该工具进行勘探圈闭风险评估的实操工作流程，它包括两个方面：一是针对成功概率和含风险概率资源量的评估流程，二是针对含风险概率资源量的期望价值评估流程。

在评估过程中，本文提出钻井数量、成功概率的相关性及钻井顺序对最终的投标决策至关重要，如何准确合理地分析和判断这3种因素对期望价值的影响决定了最终投标决策的方向。由于期望价值是成功价值和失败价值的综合体现，所以在最终决策时，应综合考虑成功概率以及失败价值的承受能力的影响，而不能一味寻求期望价值的最大化。