基于ISIGHT的轨道板运输车可靠性优化设计

王道成

（中铁四局集团有限公司第八工程局公司，安徽 合肥230041）

0 引言

图1所示轨道板运输车是用于在城市地铁及铁路上运输无砟轨道板的机械设备[1-2]，其主要结构包括T型轮架、传动系统、控制系统和司机室等，整车高1.54 m，长12.6 m，宽2.5 m，其前后轮组轴距B为7 m。轨道板运输车的工作原理是通过传送带装载轨道板，由液压支撑系统固定，防止其在运输过程中发生滑移，运输到指定位置后由传送带卸载轨道板。

轨道板运输车作为一种大型机械设备，结构复杂，设计多依赖于经验，为保证整车运输安全性，其刚度、强度均有较大的富余量，造成材料浪费，因此有必要对其结构进行可靠性优化设计。本文基于多学科优化软件ISIGHT中6 Sigma质量优化理论，在保证轨道板运输车可靠性的条件下，对其结构进行优化设计。

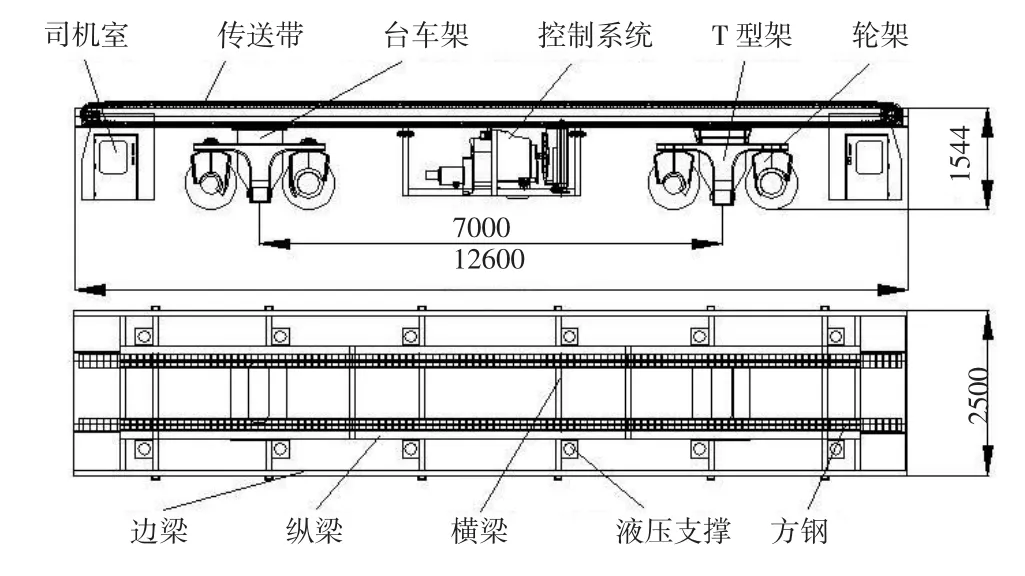
图1 轨道板运输车结构简图

1 轨道板运输车结构6 Sigma分析

轨道板运输车采用材料为Q345钢，材料许用应力[σ]=257 MPa，许用静刚度[f]=B/900=7.78[3]，取以下两种工况：

工况1：载荷作用于传送链条上，校核强度；工况2：载荷作用于传送链条上，校核刚度。

为验证轨道板运输车初始设计的可靠性是否满足设计要求，需对其结构模型先进行6 Sigma质量分析。

1.1 建立有限元模型

采用APDL语言建立轨道板运输车有限元参数化模型，如图2所示。由于整车结构简化成板结构和梁单元，因此采用ANSYS中壳单元SHELL63及实体单元SOLID95模拟。整个系统离散成181 713个单元，212 519个节点。

图2 轨道板运输车有限元模型

1.2 6 Sigma设计方法

6 Sigma设计方法（Design For Six Sigma，DFSS）是在设计初期考虑不确定性因素对产品的影响，通过概率统计的方法控制满足条件的设计变量[4]。其中σ表示标准差，反映一组数据的离散程度。计算公式如下：

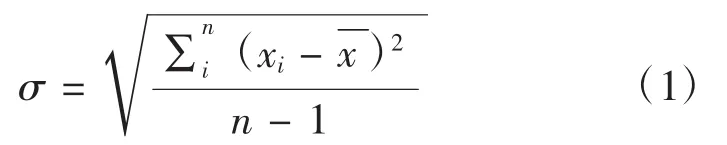
式中，n—样本容量；

xi—第i个样本的观察值；

鲁迅对国民性的改造是以暴露农民身上的弱点为切入口的，从而推及其他群体直至全体国民。鲁迅笔下的阿Q这一农民身上几乎具有所有国民性的弱点，他愚昧无知，麻木不仁，封建落后，自欺欺人。其中以“精神胜利法”最为典型。作者对阿Q这一形象的批判是十分尖锐，不留情面的。试想：如不敢揭示疮疤，像阿Q那样习惯忌光忌亮，“用瞒和骗，造出奇妙的逃路来，而自以为正路，在这路上，就证明着国民性的怯懦、懒惰、而又滑。一天一天的满足着，即一天一天的堕落着，但又觉得日见其光荣。”那么中国人民就要继续做帝国主义、封建统治者的奴隶，而且心安理得地活下去。

x—样本平均值。

6 Sigma是评价产品可靠性的重要指标，计算公式如下：

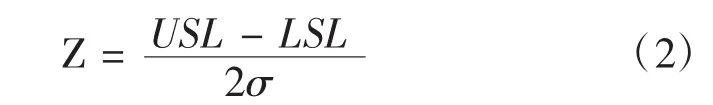
式中，USL—可接受质量的约束上限；

LSL—可接受质量的约束下限；

σ—标准差。

1.3 蒙特卡洛抽样技术

蒙特卡洛模拟（Monte Carlo Simulation，MCS）是一种以概率统计为指导的一类数值计算方法。在ISIGHT中，蒙特卡洛抽样技术是最精确的质量分析方法。为了保证计算精度，本文采用简单随机抽样的采样规则，随机抽取1 000个样本点来分析计算，采样如图3所示。

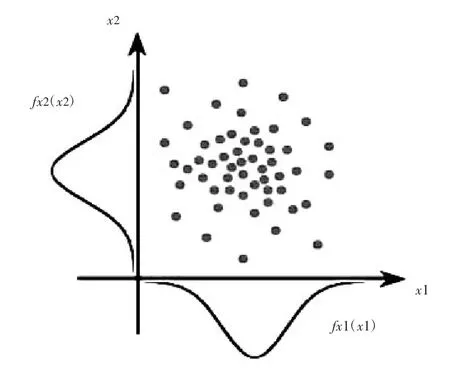
图3 简单随机抽样图示

1.4 不确定性因素

本文主要考虑的不确定性因素有尺寸及板厚偏差、载荷波动和材料弹性模量的波动。变量均值与标准差如表1所示。

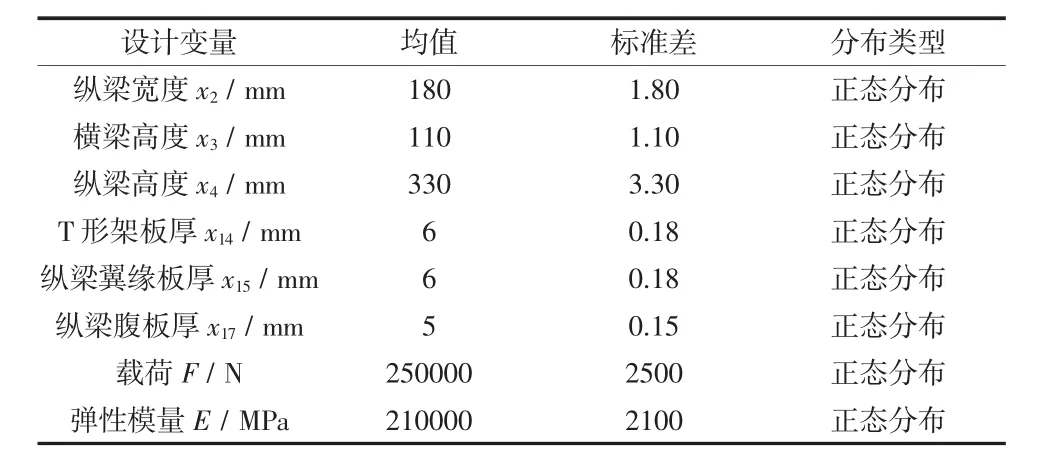
表1 不确定性因素均值与标准差

1.5 轨道板运输车神经网络近似模型

本文采用径向基神经网络构建轨道板运输车近似模型，提取200个样本点构建基函数，在误差分析过程中随机选取40个样本点，其中基函数计算公式为：

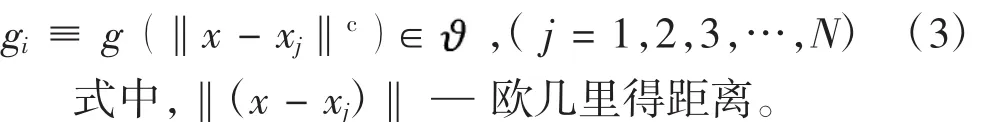
轨道板运输车神经网络近似模型误差评估结果如表2所示，各项误差指标均在其许用值内，表明其仿真精度较高，该近似模型可以替代有限元模型。

表2 近似模型误差评估结果

1.6 轨道板运输车6 Sigma分析流程

首先确立轨道板运输车的不确定性因素，并将有限元参数化模型集成到多学科优化软件ISIGHT中，然后构建径向基神经网络近似模型，通过蒙特卡洛模拟对设计变量进行简单随机抽样，最后采用6 Sigma模块分析结构模型的可靠性。轨道板运输车6 Sigma分析流程如图4所示。

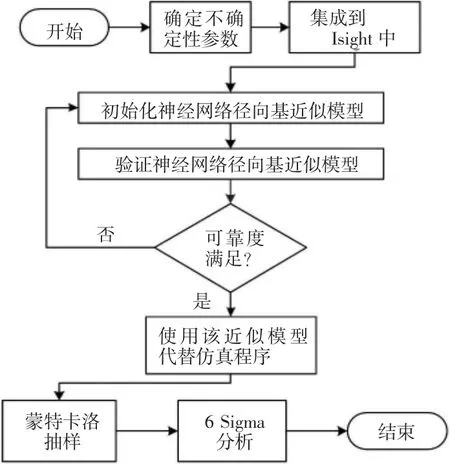
图4 轨道板运输车6 Sigma分析流程

1.7 轨道板运输车6 Sigma分析结果

通过ISIGHT分析计算得到各工况条件下的6 Sigma水平图，如图5所示；各工况的概率分布图，如图6所示。

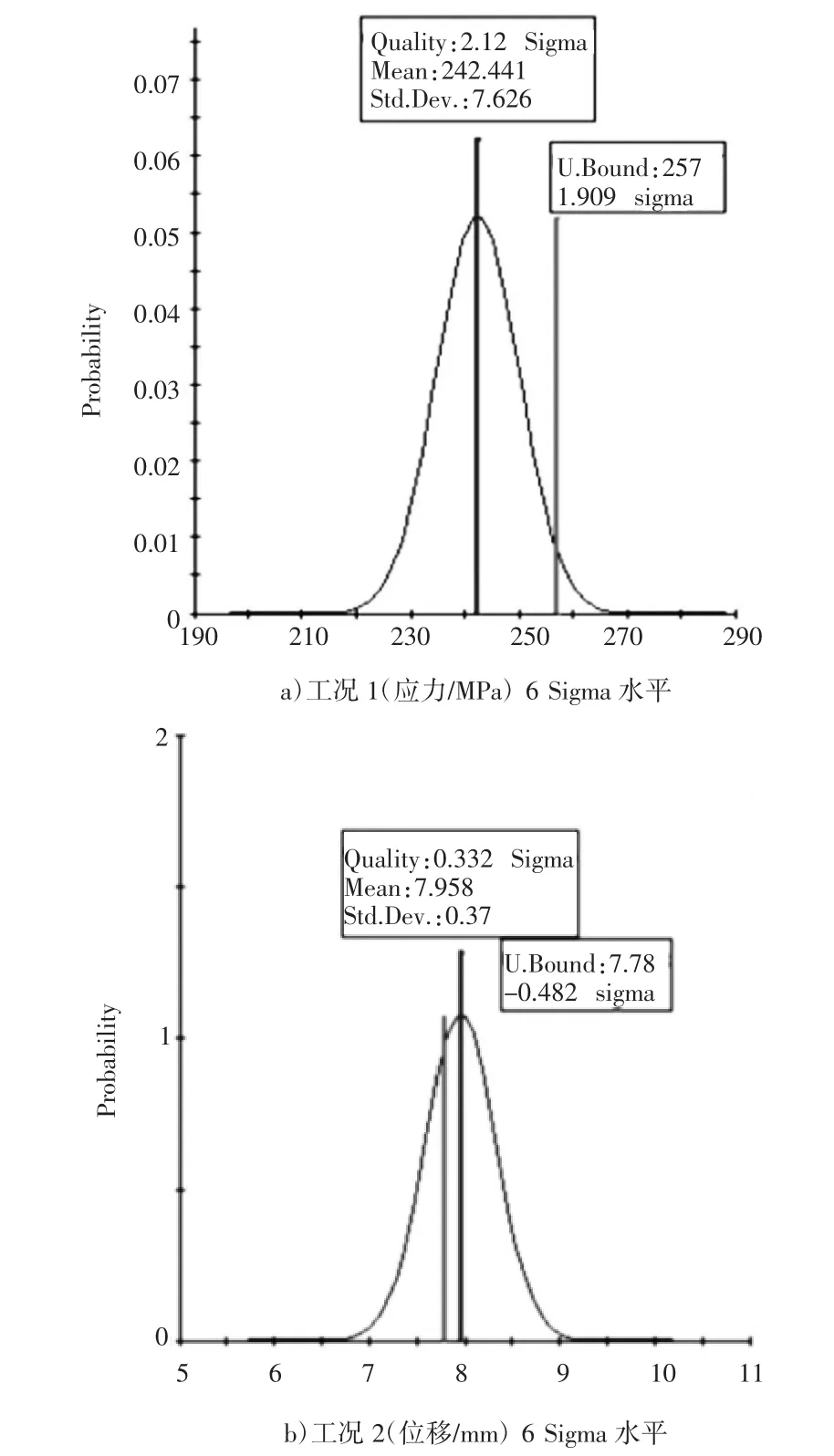
图5 各工况6 Sigma水平图

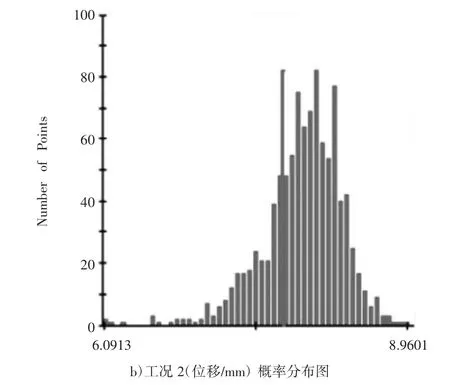
图6 各工况概率分布图

由图6可知，轨道板运输车在不确定性因素的影响下，工况1最大应力为268.57 MPa，大于材料许用应力257 MPa；工况2最大位移为8.96 mm，大于材料许用静刚度7.78 mm，因此，初始设计的轨道板运输车的可靠性不满足设计要求，需要对其进行优化设计。

2 轨道板运输车结构6 Sigma优化

2.1 轨道板运输车6 Sigma优化流程

首先定义轨道板运输车神经网络近视模型，在初始设计阶段考虑不可控因子对结构的可靠度影响；通过蒙特卡洛模拟，测量输出响应的6 Sigma水平，然后分析输出响应是否满足质量要求，若不满足要求，则通过改进设计变量均值，直到满足规定的可靠性要求。优化流程如图7所示。

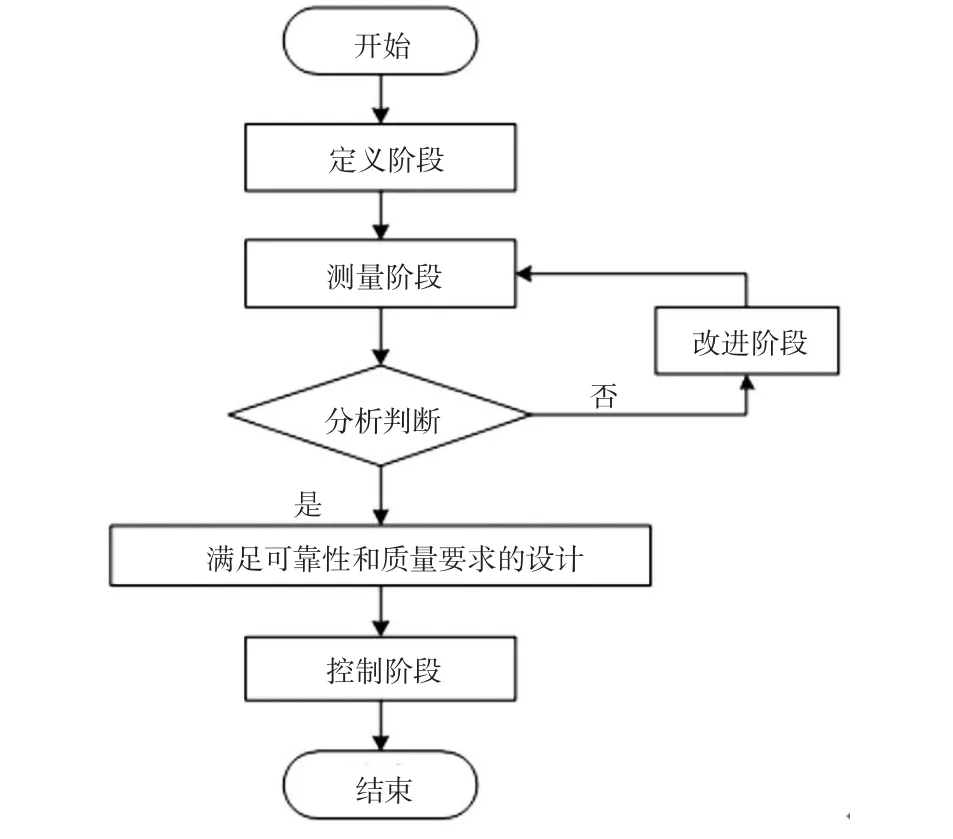
图7 轨道板运输车6 Sigma优化流程

2.2 轨道板运输车6 Sigma优化结果

通过ISIGHT软件中的优化模块分析计算得到各工况条件下的6 Sigma水平图，如图8所示；各工况的概率分布图，如图9所示。

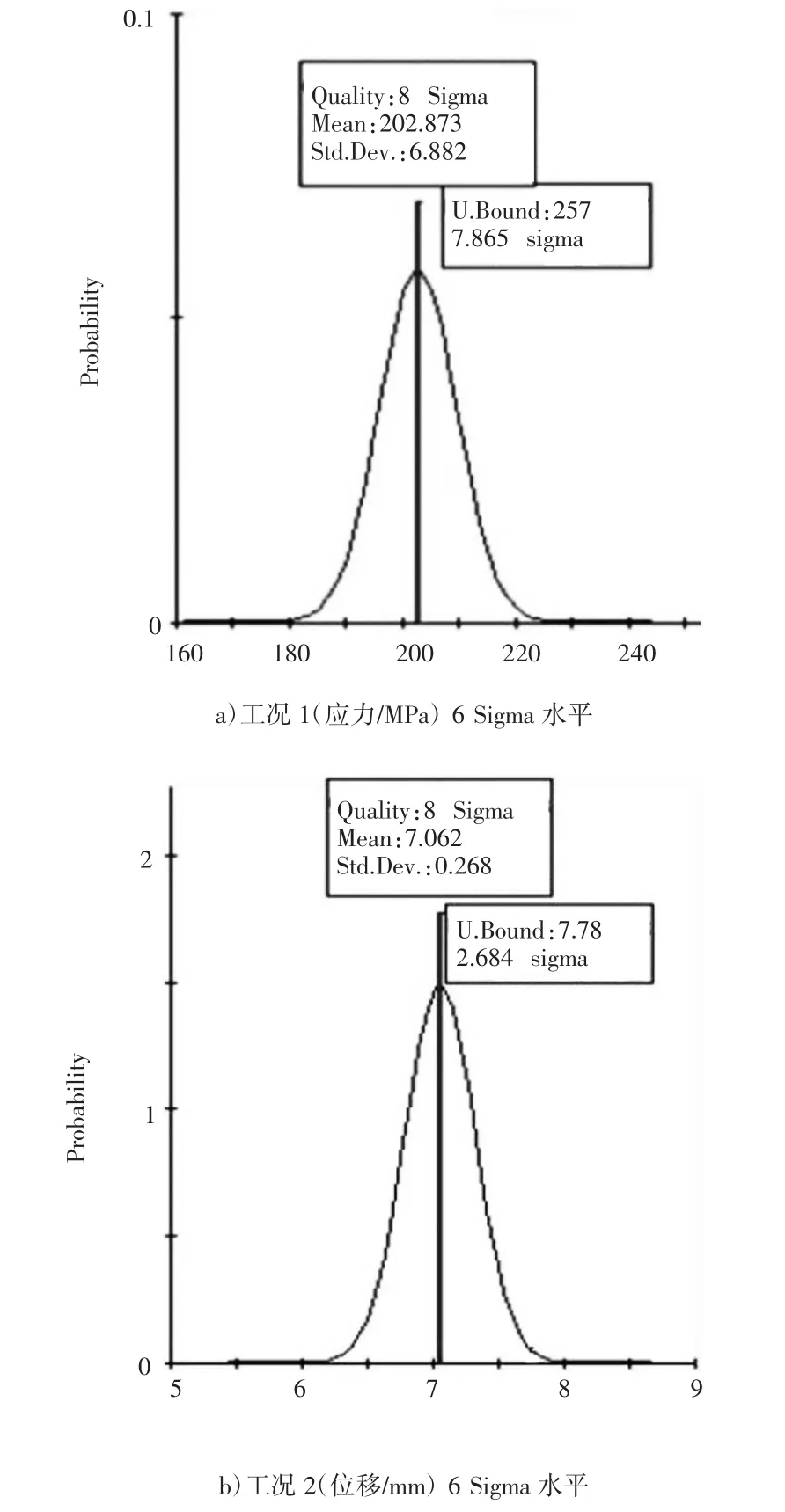
图8 各工况6 Sigma水平图

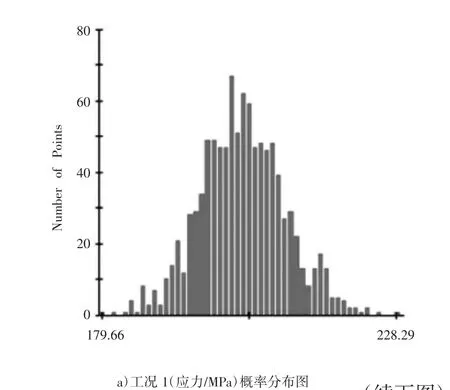
图9 各工况概率分布图

由图8可知，轨道板运输车各工况条件下的6 Sigma水平均为8.0，可以认为可靠度近似为1，满足可靠性要求；由图9可知，工况1最大应力为228.29 MPa，小于材料许用应力257 MPa，工况2最大位移为7.67 mm，小于材料许用静刚度7.78 mm，因此，优化后的轨道板运输车满足可靠性设计要求。

2.3 轨道板运输车ANSYS验算结果

由表3可知，轨道板运输车结构的自重ANSYS验算值与6 Sigma优化值差值较小，可以认为近似模型比较精确[7-8]。优化后轨道板运输车在保证满足可靠性要求的条件下，结构自重减小1 900.58 kg，与优化前质量相比自重降低了13.89%，优化效果显著。

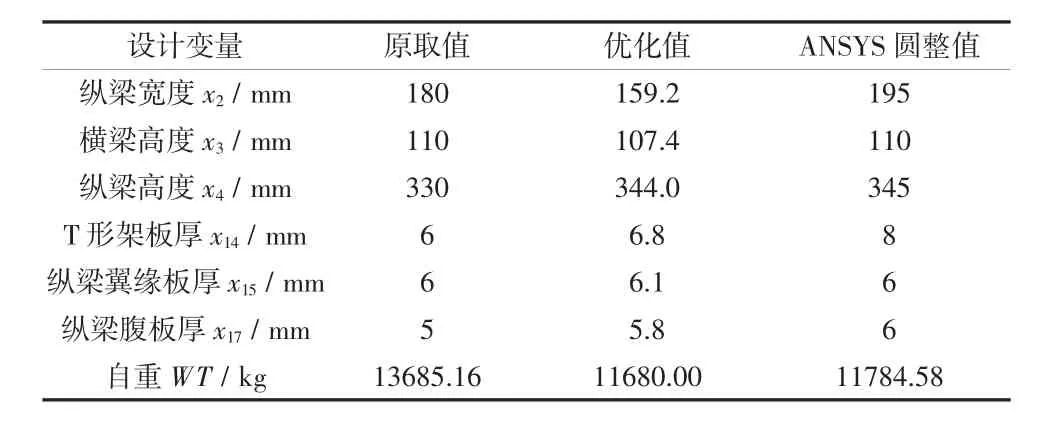
表3 ANSYS验算结果

3 结语

（1）考虑了板厚偏差、载荷波动等噪声因子对轨道板运输车结构可靠性的影响，并建立了有限元模型。

（2）在ISIHGT软件中建立了径向基神经网络近似模型，通过蒙特卡洛模拟，对原始设计的轨道板运输车结构进行了6 Sigma质量分析，结果表明，轨道板运输车在额定载荷的作用下，材料强度、静刚度均不满足可靠性设计要求。

（3）在对轨道板运输车6 Sigma质量分析的基础上进行了6 Sigma质量优化，结果表明，在满足设计可靠性的条件下，轨道板运输车结构自重降低了13.89%，优化效果显著。