函数与数列相结合的几类题型解法探究

江秋煜

(广东省广州市增城区永和中学 广东 广州 510000)

引言

在高中阶段的数学中，数列是单独作为一个章节进行教学，在数学的高考试卷中占有相当重要的比例，从选择、填空到解答，甚至一些省市的压轴题都是关于数列的问题。数列作为一个重要的知识点，能够与高中数学中许多其他的知识点相结合起来，例如未知方程、三角函数以及不等式等，都可以很好的与数列结合起来，将数列作为解题的背景。本文主要是通过举例说明函数思想在巧妙处理数列问题中所发挥的关键作用。——包括了对数函数与数列相结合，导函数与数列相结合，周期函数与数列相结合，函数图象与数列相结合来进行论述。

1.运用对数函数解决数列问题

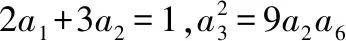
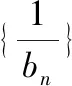
【分析】：(1)因为{an} 是各项均为正数的等比数列

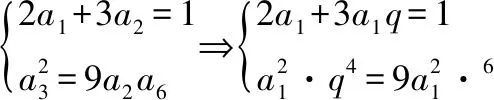
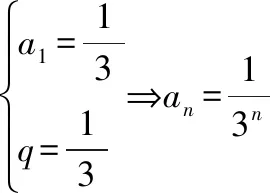
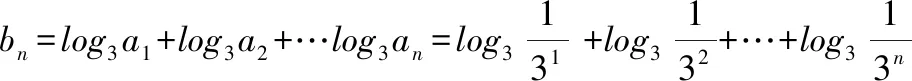
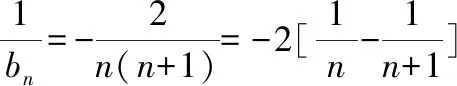
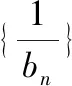
【考点解析】(1)掌握对数基本运算；(2)会等差数列求和；(3)会裂项相消法求和。

2.导函数性质解决数列问题

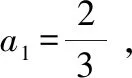
求数列{an} 的通项公式和前n项和公式Sn

【分析】因为f′(x)=3x2，所以切线的斜率为k=f′(1)=3，而切点(1，2)，

切线方程为y-2=3(x-1) ，即：y=3x-1

又因为切线经过点(an+1,an) ，所以an=3an+1-1 ，即3an+1=an+1 ①

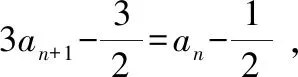
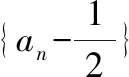
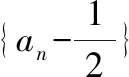
3.运用周期函数性质解决周期数列问题

【例题】设数列{an} 中，a1=a2=1，a3=2,且对n∈N，有anan+1an+2an+3=an+an+1+an+2+an+3(anan+1an+2≠1)成立，试求该数列前100项和S100．

【分析】：对任何自然数N+，有anan+1an+2an+3=an+an+1+an+2+an+3①

把式中的n换成n+1 ，得an+1an+2an+3an+4=an+1+an+2+an+3+an+4②

①-②得an+1an+2an+3(an-an+4)=an-an+4．

由于an+1an+2an+3≠1 ，必有an+4=an(n∈N+) ．

所以数列{an} 是以4为周期的周期数列.所以S100=25S4=25×(1+1+2+4)=200 ．

选取2015年10月～2018年1月吉林省辽源市矿业集团有限责任公司职工总医院收治的60例桡骨远端骨折患者做为研究对象，分为观察组和对照组2组，每组30例，观察组中男14例，女16例，年龄29～66岁，平均（45.9±3.2）岁，部位：左侧18例，右侧12例；对照组中男13例，女17例，年龄27～65岁，平均（45.6±3.6）岁，部位：左侧19例，右侧11例。两组患者的性别、年龄、部位等资料比较，差异无统计学意义（P＞0.05）。

【考点解析】：(Ⅰ)能够根据数列递推条件把式中的n换成n+1 ；(Ⅱ)能够通过数列的一些基本技能得出“an+T=an”，从而确定该数列具有周期性，并确定周期值。

4.运用函数图像直观地分析数列问题

【例题】已知{xn} 是各项均为正数的等比数列，且x1+x2=3,x3-x2=2

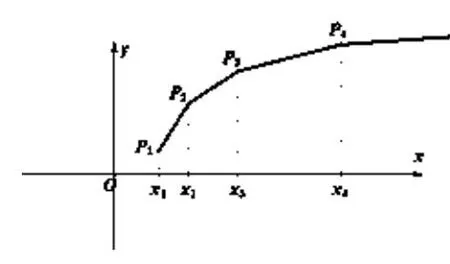
(Ⅰ)求数列{xn} 的通项公式；(Ⅱ)如图，在平面直角坐标系xoy中，依次连接点P1(x1,1) ,P2(x2,2) ,P3(x3,3) ,…,Pn+1(xn+1,n+1) 得到折线P1P2P3…Pn+1，求由该折线与直线y=0，x=x1,x=xn+1所围成的区域的面积Tn.

【分析】(I)设数列{xn} 的公比为q(q>0) .

由x1+x2=3

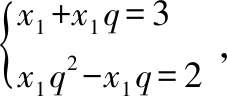
所以3q2-5q-2=0，解得q=2，x1=1 .

所以数列{xn} 的通项公式为：xn=2n-1.

(II)过P1,P2,P3, ……Pn+1向轴作垂线，垂足分别为Q1,Q2,Q3, ……Qn+1,

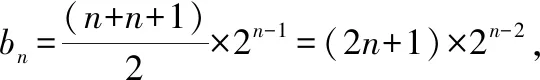
所以Tn=b1+b2+b3+ ……+bn

=3×2-1+5×20+7×21……+(2n-1)×2n-3+(2n+1)×2n-2

①

又2Tn=3×20+5×21+7×22+ ……+(2n-1)×2n-2+(2n+1)×2n-1

②

①-②

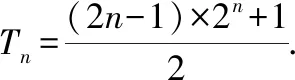
【考点解析】本题通过的图象模型性质，巧妙的把平面几何区域面积转化为数列求和问题。

5.构造特殊函数模型解决数列问题

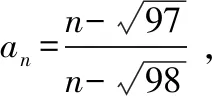
A、a1,a30B、a1,a9C、a10,a9D、a10、a30

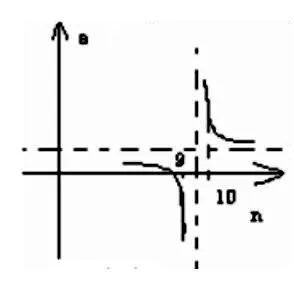
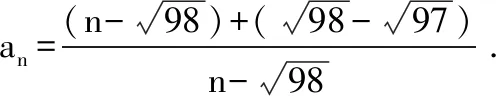
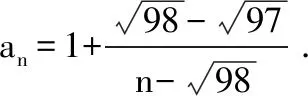
【考点解析】：本题通过函数思想，把数列问题通过分离常数，把数列问题转化成熟悉的函数模型，结合函数模型的图像性质解决问题。

数列知识是高中数学的重要组成部分，更是学习高等数学的基础，所以在近年的高考中，它都占有非常重要的地位.高考对数列知识的考查比较全面，等差数列，等比数列的考查每年都不会通过不同的形式呈现.解答题多以中等难度为主，突出考查考生的严谨的思维能力和解决问题的能力，试题大多有较好的区分度，而其中数列知识和函数知识相互渗透，交叉命题已成为近年高考的热点，常在数列解答题中出现。