单自旋翻转的一维吸引费米气体
2019-05-31张瑞江尹相国陈立张云波
张瑞江,尹相国,陈立,张云波
(山西大学 理论物理研究所,山西 太原 030006)
0 引言
近年来对费米子捕获和冷原子的操纵取得了很大的实验进展[1-3],其中在自旋向上的费米子组成的费米海中加入一个自旋向下杂质粒子的系统受到学者们的青睐[4-5]。在弱吸引相互作用下,杂质粒子与每一个自旋朝上的费米子都存在弱的耦合,形成了费米极化子。随着吸引相互作用强度的增加,杂质会经历一个从极化子到分子态的过渡过程。为了研究系统的结构以及其他性质,我们引进关联函数,关联函数可以用来刻画量子系统的多体效应[6]。2015 年,Patu 以及Klumper 等人研究了非均匀一维旋量玻色气体的热力学、密度分布和关联函数[7],文献[8]在有限温度下精确求解了一维玻色气体在简谐势阱中的密度关联函数。一些实验小组在一维和三维的玻色系统中测量了两粒子和三粒子的关联[9-12]。一维相互吸引费米气体的单体和二阶关联也受到许多人的关注[13]。关联函数主要包括相位关联[14]、动量空间的关联[13]和坐标空间的关联[15]。
本文主要研究一维吸引相互作用的费米气体模型中的关联函数。首先,我们给出了系统的哈密顿量,从Bethe-Ansatz(BA)方程出发写出了一次量子化波函数的严格解。然后从二次量子化的波函数出发,推导出系统的单体关联函数和二阶关联函数。我们数值求解BA方程,给出单体关联函数和二阶关联函数的数值结果。
1 理论模型
一维Gaudin-Yang模型在自然单位制下(ћ=2,m=1)的哈密顿量可以写为:
(1)
其中,第一项为动能,第二项是粒子间的相互作用能,相同自旋粒子之间没有相互作用,不同自旋粒子之间才有相互作用。N是系统粒子总数目,i表示粒子的标号,xi表示第i个粒子所处的位置,2c是相互作用常数。当c>0时,粒子间存在排斥相互作用,当c<0时,粒子间为吸引相互作用。在本文我们主要讨论c小于0也即相互吸引的情况。考虑特殊情况,系统中只有一个自旋向下的粒子,其余粒子都自旋向上,就可将该自旋向下的粒子视为杂质[16]。文章考虑的是一维系统,所以在弱吸引相互作用下只有极化子,不考虑库伯对的情形。图1给出了弱相互作用下的极化子到强吸引相互作用情况束缚分子的示意图。

Fig.1 Schematic configuration of the polaron-molecule crossover of a single attractive impurity in the 1D Fermi gas.In the weak interaction, the impurity is dressed by the surrounding scattered particles in Fermi sea.In the strong interaction, the impurity binds with a particle in Fermi sea to become a molecule of two atoms.在弱相互作用下,杂质粒子被费米海粒子所包围,在强相互作用下,杂质粒子和费米海中的某个粒子束缚成两个粒子组成的分子态。图1 一维费米气体中杂质从极化子到分子的示意图
本文先介绍极限情况的一次量子化波函数。当相互作用常数c为0时,系统可视作由N-1个粒子组成的费米海和独立杂质构成。我们采用周期性边界条件,并且粒子不受外势,所以单个粒子的波函数就是平面波的形式。N-1个自旋相同的费米子的波函数就是平面波组成的行列式形式。所以第N个粒子自旋向下其余粒子自旋向上的波函数可以写作N-1个粒子组成的行列式与第N个粒子平面波函数直积的形式:
(2)
其中求和号是对{1,2,…,N-1}所有排列的求和。当系统处于基态时,k的值为2π/L的整数倍,当粒子数为偶数时
(3)
L表示系统的总长度,此时(2)中的kN取值为0,即向下自旋粒子的动量为0.
当相互作用不为0时,第N个粒子自旋向下其余粒子自旋向上的波函数可由BA方法得到:
(4)
此处求和号是对{1,2,…,N}所有排列的求和,而连乘号是对所有向上自旋态求积,其中c′=c/2,Λ表示自旋快度,kj表示准动量,符号函数为

(5)
kj和Λ的值由下面BA方程组[17]决定
(6)
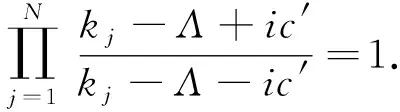
(7)
这里一次量子化波函数f↓j满足粒子交换反对称性,无论相同自旋还是不同自旋的两个粒子交换,波函数都满足粒子交换反对称性,即
f↓j(x1,…,xj,…,xN)=-f↓j(x1,…,xN,…,xj),
(8)
f↓j(…,xm,…,xj,…,xn,…)=-f↓j(…,xn,…,xj,…,xm,…).
(9)
该模型的二次量子化的系统总波函数可以写为
(10)

(11)
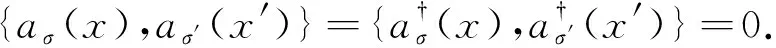
(12)
2 关联函数
我们从二次量子化的波函数出发,推导用一次量子化波函数表示的单体关联和二阶关联函数。在计算系统的关联函数之前,我们首先需要计算波函数的归一化因子。
2.1 归一化因子
归一化因子是通过对二次量子化波函数求内积得到的
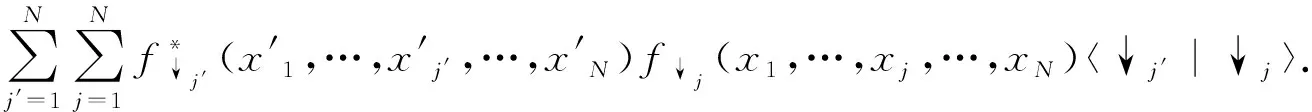
(13)
计算的核心是求内积〈↓j′|↓j〉,将基矢写成算符作用到真空态上之后,为了计算方便,我们将自旋向下的产生算符移动到两端,剩余自旋向上的算符中自变量由于缺少了一项,将之用一套新的符号表示,令
(14)
{x1,…,xj-1,xj+1,…,xN}={y1,…,yN-1}.
(15)
此时基矢内积可以写作
(16)
通过将湮灭算符逐个移至产生算符的最右端,得到该内积计算结果为
(17)
式中的P表示对所有自旋向上的N-1个粒子全排列。同样的道理,将所有产生算符左移到湮灭算符的最左端,该内积结果可表示为
(18)
在(18)式代入(13)式之前,先把系数中自旋向下坐标都移到两端,然后利用δ函数的性质,计算整理得
(19)
令〈ftot|ftot〉=1,容易得到归一化因子为
(20)
2.2 自旋向上费米子的单体关联函数
单体关联函数表明了在x′位置湮灭一个粒子的同时在x位置产生该粒子的概率,是研究一个系统的重要物理量。自旋向上费米子的单体关联函数定义为
(21)
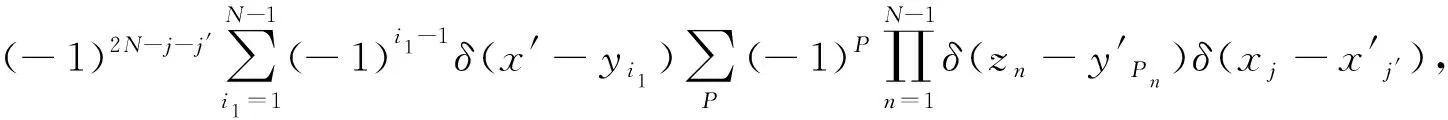
(22)
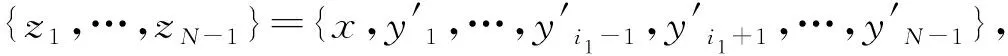

(23)
将上式中的坐标{yk}换回到{xk′},再将归一化系数代入该式,容易得到
(24)
利用波函数的交换反对称性,上式可以化简为
(25)
该式即为单体关联函数的表达式。
2.3 二阶关联函数
二阶关联函数是我们研究的另一个兴趣,在x′位置发现一个粒子的同时在x位置发现另一个粒子的概率。向上自旋的二阶关联函数为

(26)
(27)
上式中p1是由于第一个湮灭算符作用到基矢真空态的过程中使得基矢中产生算符减少一项,第二个湮灭算符作用时出现δ函数正负号发生紊乱,为了调节正负号,此处引入因子(-1)p1,使正负号恢复原来的规律,其取值如下:
(28)
(27)式中,
(29)
将(27)代入(26)式,利用(29)式将zn还原成yn表示的形式,然后再利用(15)将自变量还原成xn的形式,最后将归一化因子代入得到
(30)
利用波函数的交换反对称性,上式可以化简为
(31)
利用相同的推导办法得到上下粒子之间的二阶关联函数表达式为
(32)
3 数值求解BA方程
单自旋翻转费米系统中,假定杂质和其中一个自旋向上的费米子动量的解为弦解,即准动量用p±iβ来表示,p是准动量的实部,β是准动量的虚部,将之代入BA方程组(6),两式同时化简整理得:
(33)
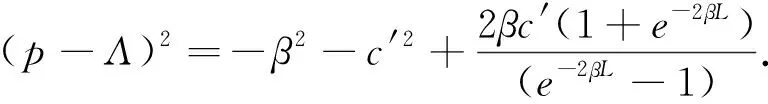
(34)
再将(6)中剩余的N-2个实数准动量方程两边同时取对数得
(35)
将所有准动量代入方程(7),两边同时取对数得
(36)
把方程组(33)到(36)利用数值求解得到所有动量和自旋快度的值。
但是对于强吸引的情况下,以上方程数值解并不精确,因为(36)式中β+c′趋向于0,同时分子也趋于0,所以无法数值精确解。此时我们发现(33)式给出p=Λ=0,从(34)式可以得到
(37)
同时,方程(35)变成
(38)
据(37)和(38)即可解得强吸引相互作用下的准动量值。将这些值代入波函数,进而利用(25)、(31)和(32)计算关联函数。
4 结果分析
选取系统的粒子数为N=8,将x′固定在0.5处,利用蒙特卡罗方法计算多重积分,我们给出相互作用强度从0到-1 000的单体关联函数的图像(见图2)。当吸引相互强度非常小时,从BA方法得到的单体关联函数和无相互作用下的费米波函数得到的曲线符合得非常好,印证了两个波函数的一致性。当相互作用比较弱时,单体关联函数没有明显变化。原因是自旋朝上的费米子之间受泡利不相容原理的限制彼此之间无相互作用,只与自旋朝下的单杂质之间存在相互作用,因而相互作用对自旋朝上费米子的单体关联函数影响非常有限。当相互作用非常强时,峰值部位变得越来越窄,即短程关联以更快的速率衰减,说明强吸引会使单个粒子被观察到高概率的范围变小。
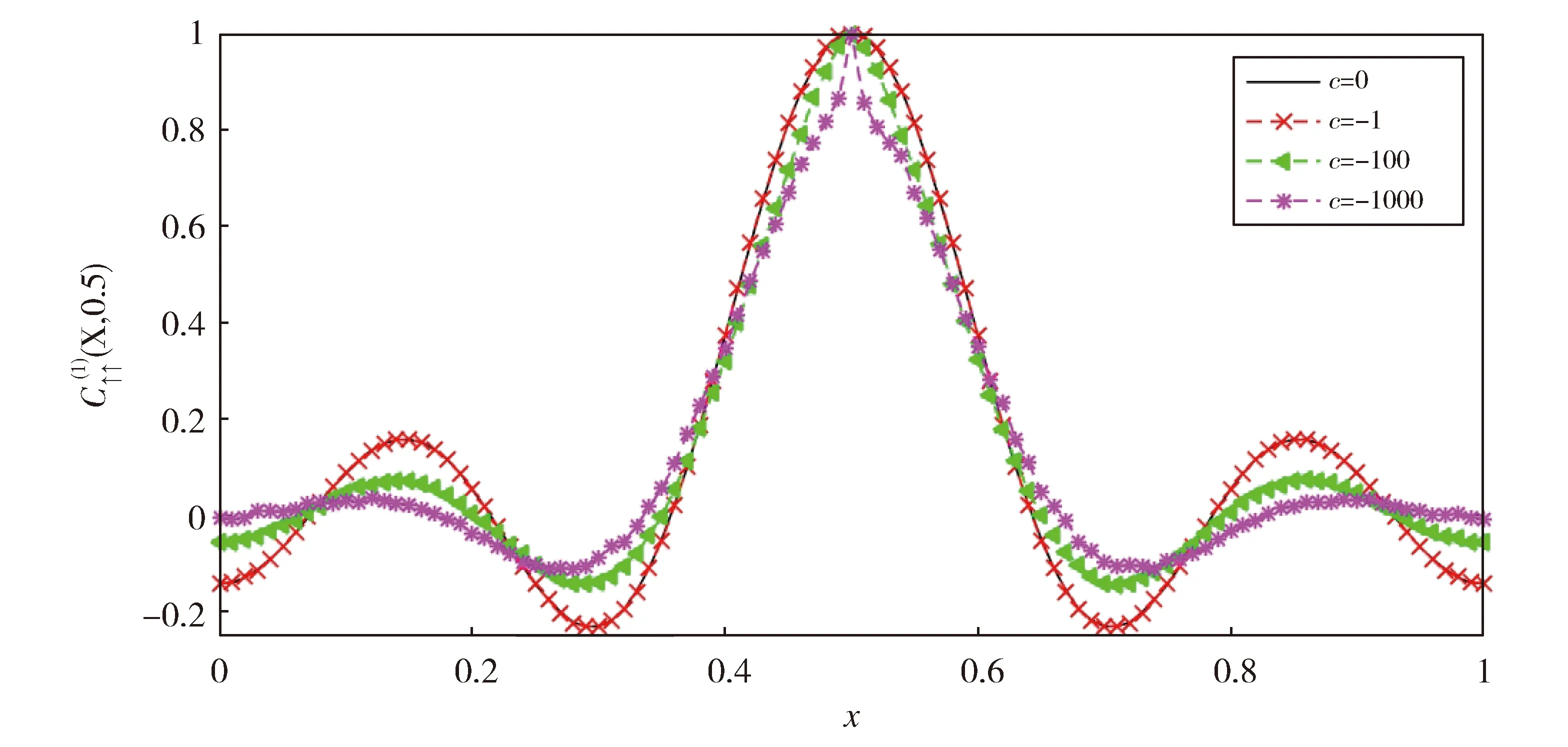
Fig.2 One body correlation function of the up spins in the ground state Here we chooseL=1 andN=8这里选取L=1和N=8图2 基态向上自旋单体关联函数
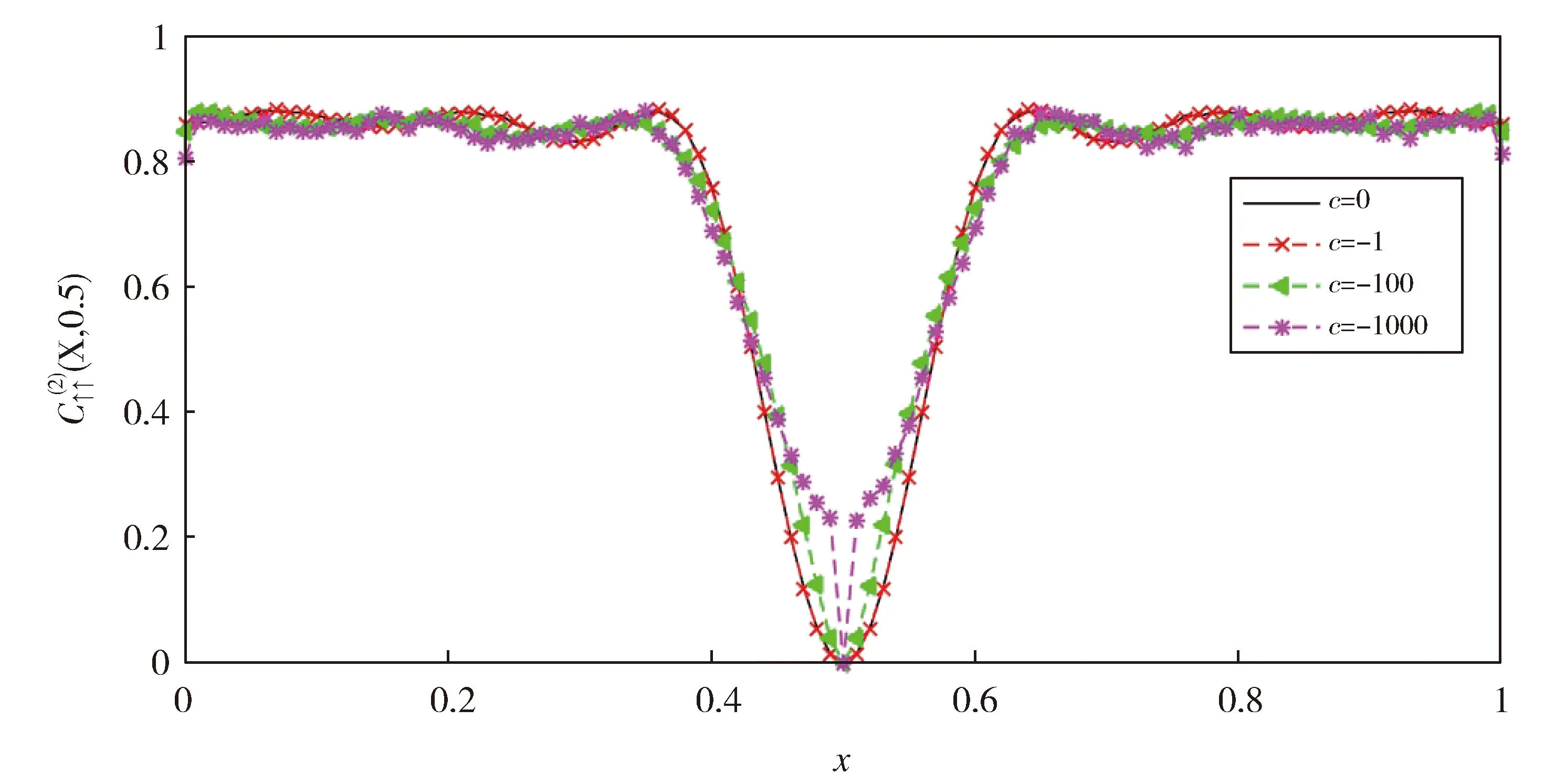
Fig.3 Second order correlation function between up spins in the ground state Here we chooseL=1 andN=8图3 基态向上粒子间二阶关联函数这里选取L=1和N=8
同样利用蒙特卡洛方法计算多重积分,我们给出了自旋向上的两个粒子间二阶关联函数(图3)。x=0.5的值为零,表明两个相同自旋的费米子不能占据同一个位置。对于无相互作用的系统,关联函数出现周期性振动,并呈现6个峰值,表示在这些峰值处观察到粒子的概率最大。因为一个自旋朝上的粒子固定时,剩下的只有6个自旋朝上的粒子,所以有6个峰值。随着相互作用强度的增加, 关联函数中在x′位置附近图像变的越来越窄,但总体趋势保持不变。
相同的数值方法得到上下自旋粒子之间的二阶关联函数图像,如图4所示。令x′=0.5,即在0.5处固定一个自旋向下的粒子,通过图中可以看到,随着相互作用强度的增加,在x=0.5的位置慢慢开始突起,且越来越高,其余地方几乎是一条直线,意味着系统形成了极化子并向紧束缚分子态的转化。
5 结论
我们讨论了含单个费米杂质的费米气体的单体和二阶关联函数。通过极化弱相互作用和无相互作用情况的比较,证实了BA方程得到的波函数和理想费米气体波函数的一致性。弱相互作用下,单体关联函数和二阶关联函数都没有明显的变化,与理想费米气体的性质一致。当相互作用很强时,单体关联函数和向上自旋之间的二阶关联函数的尖端变得越来越窄,但整体趋势保持不变;而对于上下自旋粒子间的二阶关联函数,随着相互作用的增强,关联性更强,系统在相互作用增强的情况下,形成了极化子,并向紧束缚分子态转化。
