基于S变换的高速列车小幅蛇行识别方法
2019-05-31种传杰陈春俊
宁 静 冉 伟 种传杰 陈春俊
西南交通大学机械工程学院,成都,610036
0 引言
高速列车运行过程中的横向稳定性至关重要。由于列车轮对具有一定的锥度,因此即使车辆沿平直的轨道运行,只要有一个初始激励,轮对就会绕轨道中心线一边横移一边摇头向前耦合运动,即产生蛇行运动[1]。若车辆以较高的速度运行,则当蛇行运动频率与车辆自振频率接近时,其振幅不断扩大,这时的蛇行运动就丧失了稳定性,即发生了蛇行失稳,且幅值增大越快,失稳的程度就越严重。
在列车实际运行过程中,基于轨道不平顺和车轮磨损等原因,当列车速度小于蛇行失稳理论临界速度时,就有可能发生失稳现象[2]。笔者在对某型高速列车的在线跟踪试验数据进行分析时发现[3],列车在时速超过300 km/h运行时易出现小幅蛇行运动,且有的小幅蛇行出现后会紧接着出现蛇行异常。考虑到小幅蛇行可能会导致蛇行异常,因此,非常有必要对小幅蛇行进行监测,进而及早采取措施消除小幅蛇行,以保证高速列车的安全运行。
国内针对小幅蛇行的监测进行了一些研究。蔡里军[2]认为,转向架横向振动加速度峰值出现连续6次以上达到或者超过极限值2 m/s2(现有标准为8~10 m/s2)且符合相关条件时,在工程上即可判定转向架发生蛇行运动失稳,但此判据是完全依据多次蛇行异常的在线测试数据以及工程实践经验得出的,没有对小幅蛇行现象进行相关的理论研究,此结论是否具有普遍意义,还需要进一步探讨与验证。孙丽霞[4]从提高车辆横向稳定性安全裕量的角度,通过计算高速列车转向架构架横向振动加速度均方根值,提出了一种监测转向架小振幅蛇行振动的方法。但此类方法对监测数据采取的数据处理方法都是基于平稳数据的,没有考虑高速列车振动信号的非平稳特性。
高速列车的横向稳定性系统特征具有很强的非平稳和非线性特征,可以认为列车在线监测数据的本质为时变系统在非平稳激励作用下的非平稳、非线性、多信号的输出,因此,使用传统的平稳信号处理方式研究高速列车的蛇行运动相关问题显然是不合适的。考虑到通过现有的跟踪监测设备[5]能够方便地获得高速列车运行时的转向架横向加速度信号,本文使用基于时频分析的信号处理方法提取列车小幅蛇行特征,从而预测蛇行运动,保障列车运行安全。S变换[6]是基于小波变换和短时傅里叶变换的一种时频分析方法,它结合了短时傅里叶变换(short-time Fourier transform, STFT)和小波变换(wavelet transform)的优点,并且具有相位信息。
本文提出利用S变换对高速列车转向架横向加速度信号进行特征提取,对经过S变换得到的复时频矩阵进一步取模得到模时频矩阵,提取模时频矩阵最大能量对应频率处的时间-幅值特征函数Vf(t),然后对此特征函数提取4种简单的特征指标,最后采用最小二乘支持向量机(least square support vector machine, LS-SVM)识别出正常、小幅蛇行以及蛇行异常3种不同的运行状态。
1 试验数据
经跟踪观察,某型高速列车在某线路运行的过程中易出现蛇行异常振动。针对此情况, 2011年3月12日至2011年4月20日期间对运行在该区间的列车进行了专门的跟踪试验[7]。本次试验在转向架上安装了加速度传感器,加速度传感器的型号为LC0709A-18,量程为(-18~18)g,速度信息通过GPS系统采集。
对跟踪试验数据进行分析时发现,当列车运行速度在340 km/h左右且未见明显增大的情况下,某型高速列车的转向架横向加速度信号还易出现幅值较小的极限环——小幅蛇行现象。在这种情况下,转向架横向加速度信号幅值会慢慢变大,列车运行因此会经历从正常运行到小幅蛇行,最后发散到蛇行异常的过程,如图1所示。
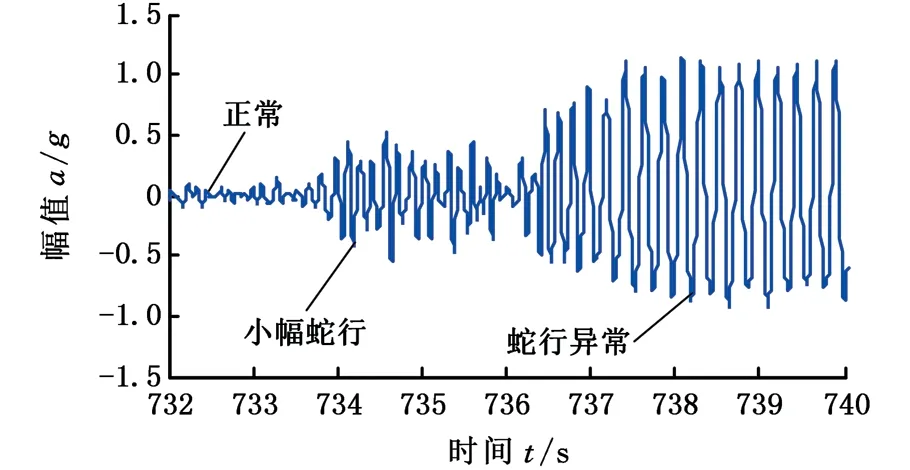
图1 一段产生蛇行运动的转向架构架横向加速度和速度数据Fig.1 A section of the hunting movement of the bogie frame lateral acceleration and speed
为研究如何准确识别转向架小幅蛇行,对采集到的原始信号进行分类截取。对蛇行异常振动严格按照转向架构架横向加速度幅值连续6次大于8 m/s2进行截取,横向加速度幅值小于2 m/s2即为正常运行状态,高速列车小幅蛇行数据则是加速度幅值介于2~8 m/s2之间的数据。本文对此三种状态下的转向架横向加速度信号分别选取36组样本数据,将每种状态下的36组样本数据进行归一化后,将其均分成两部分,18组作为训练样本,另18组数据作为测试样本。
考虑到在线试验成本较高,测试数据不仅用于蛇行运动分析,还可用于研究高速列车的振动演变规律研究等,设置本次试验的采样频率为2 500 Hz。由于蛇行运动本身是低频振动,为便于进行数据处理,结合香农采样定理,对数据进行250 Hz的重采样,然后进行2~12.07 Hz的带通滤波。关于数据长度的选取,考虑到样本数据过短会导致信息不完整,而样本数据过长会导致采样和计算时间增加,不利于预测和后面的控制操作。通过对大量数据观察发现,取数据段的时间长度t=2 s是符合实际情况的,2 s的数据段包含了故障状态主要时频特征,同时数据长度相对较短。因此,结合实际情况,选取250 Hz重采样后样本长度为500个的数据点(t=2 s)。
2 当前小幅蛇行监测方法
2.1 当前小幅蛇行监测理论
目前国内外对铁道客车横向运动稳定性的评定标准并未统一,相关标准中,关于监测小幅蛇行状态的评价标准均未涉及。我国铁道客车行车安全监测标准[8-9]采用的是横向加速度峰值评价法:当转向架横向加速度的峰值连续6次以上(含6次)达到或超过极限值8 m/s2时,则判定转向架横向失稳。而国外的相关评定标准[10-13]分别规定:车辆在运行过程中的轮轨横向力、轮轴横向力、转向架横向加速度及车体横向加速度不能超过规定限值,否则应减速运行,以保证列车运行的安全。例如欧盟采用的是横向加速度均方根评价法。欧盟标准的具体做法是将采集到的转向架横向加速度数据进行f0±2 Hz的带通滤波(f0为转向架的蛇行失稳频率),并在整个判定流程中设定步长为10 m,进而计算其长度为100 m的移动均方根值RMS,若此计算结果超过限值y,则判定转向架失稳,即列车出现蛇行运动。在上述判据中限值y并不唯一,而是根据车辆的转向架质量来确定,其具体的计算公式可表示为
(1)
其中,mb为转向架质量(单位为t),判定限值y的单位为m/s2。
文献[4]在欧盟标准的基础上提出了一种识别小幅蛇行的监测方法。首先通过频谱分析,确定监测信号的强迫振动频率范围[fF0,fF1]和监测信号的蛇行振动频率范围[fH0,fH1],然后计算RF和RH。其中,RF为转向架横向加速度在强迫振动频率范围[fF0,fF1]内的均方根值,RH为转向架横向加速度在蛇行振动频率范围[fH0,fH1]内的均方根值。RF和RH的计算长度均为100 m,步长为10 m。最后,根据下式判定高速列车的运行状态
(2)
一旦RF和RH都满足式(2)中的条件,则判定列车出现小幅蛇行现象。其中,α、β为阈值折减系数。与y的取值相似,阈值折减系数α和β的取值受到车辆结构和轨道不平顺的影响。式(2)可进一步表示为
(3)
此外,在上述计算过程中,[fF0,fF1]和[fH0,fH1]的取值随着车型与线路情况的变化而变化,具体的取值情况应视转向架实际的强迫振动能量和自激振动能量的主频分布范围而定。
2.2 当前小幅蛇行监测理论的局限性
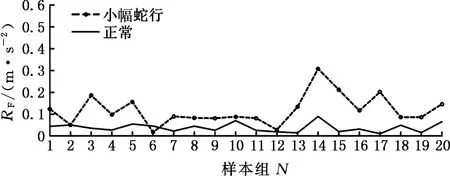
为检验现有小幅蛇行监测理论的有效性,本文利用某型车的实测跟踪数据进行验证。通过对监测数据进行频谱分析可知,该型车辆转向架横向加速度相关频率范围为[fF0,fF1]=[7,12]Hz及[fH0,fH1]=[4,7]Hz。已知该车型动力转向架质量mb为10 t,即根据式(3)可知,该车型在其运行轨道条件下,若同时满足RF≤5α和RH>5β即可判定车辆出现小幅蛇行现象。分别选取20组正常和20组小幅蛇行振动信号计算RF和RH值,计算结果如图2所示。由图2可发现,小幅蛇行和正常运行两类信号的RF值在2、6、12样本组处出现了交集(图2a);小幅蛇行和正常运行两类信号的RH值在2、10、11、13、16、17、18样本组处出现了交集(图2b)。这会导致无论如何调整α和β值,都无法把小幅蛇行和正常运行两类信号区分开来。由此可见,文献[4]提出的基于均方根值的监测方法大部分情况下能够实现对小幅蛇行的识别,但个别情况下则无法将小幅蛇行与正常状态区别开来,从而难以达到对小幅蛇行振荡进行有效监测的目的。这可能与文献[4]中,对监测数据采用的数据处理方法都是基于平稳数据的,忽略了高速列车在运行中的非平稳特性有关。
(a)RF值
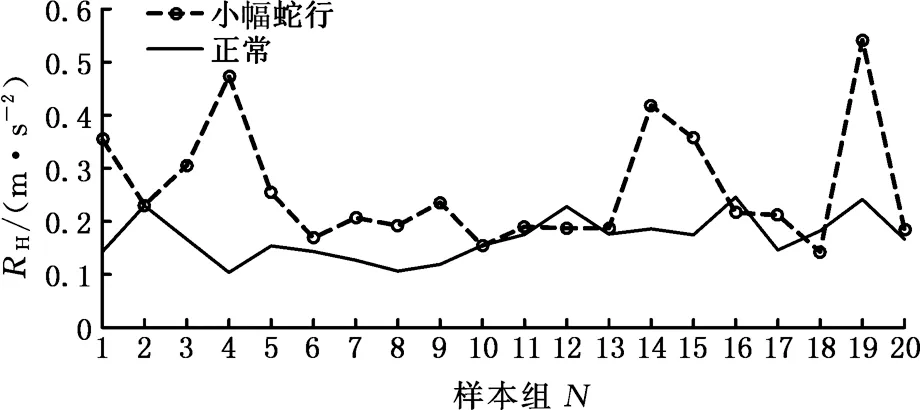
(b)RH值 图2 20组样本的RF和RH值Fig.2 RF and RH of the 20 groups of sample data
3 S变换方法
3.1 S变换方法原理
S变换是由STOCKWELL等[14]于1996年首先提出的,它是一种时频可逆分析方法,具有多分辨率分析的能力,又兼具单频率独立分析的特点。S变换可看成是小波变换的“相位修正”,也可从STFT演变而来,信号h(t)的S变换定义为
S(τ,f)=
(4)
式中,t为时间;j为虚数单位;f为频率;τ为高斯窗函数的中心位置。
由式(4)可以看出,S变换中高斯窗的宽度和高度随频率变化而变化,这样S变换就克服了STFT窗口宽度和高度固定不变的缺陷。
S变换也可写成两个函数的卷积:

(5)
p(τ,f)=h(τ)exp(-j2πfτ)
(6)
(7)
设B(α,f)为S(τ,f)的傅里叶变换(从τ到α),由卷积定理可得
B(α,f)=P(α,f)G(α,f)
(8)
其中,P(α,f)、G(α,f)分别为p(τ,f)与g(τ,f)的傅里叶变换,显然
(9)
其中,H(α+f)是式(6)中的傅里叶变换,指数项是式(7)中的傅里叶变换。因此,S变换可由式(9)的傅里叶逆变换求得(由α到τ):
(10)
故S变换可利用快速傅里叶变换实现快速计算。
令τ→iT,f→n/(NT) (N为采样点总数,T为采样周期),将信号离散化后可得离散时间序列h(kt),其中k=0,1,…,N-1,则根据式(10)可得到S变换的离散形式为
n≠0
(11)
其中,i、m、n均为从0~N-1的正整数。
h(kT)为S变换的逆变换,即
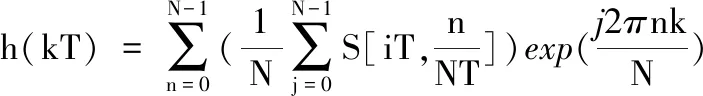
(12)
3.2 S变换处理结果及分析
以高速列车转向架横向加速度实测数据为分析对象,每组样本数据经S变换后得到一复时频矩阵S[lT,n/(NT)],其中l表示采样时刻,其行向量反映了转向架横向加速度信号某一时刻的频率分布,而列向量则反映了转向架横向加速度信号某一频率随时间变化的情况。对复时频矩阵S[lT,n/NT]中的元素分别求模后得到S变换模时频矩阵Sa[lT,n/(NT)],其表达式如下:
(13)
Sa[lT,n/(NT)] 包含了不同时间点处该矩阵在不同频率段上幅值的分布情况。
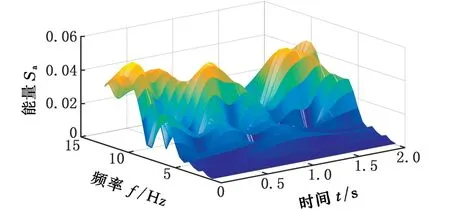
(a)正常
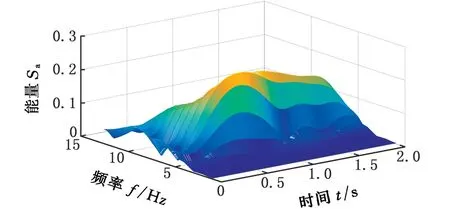
(b)小幅蛇行
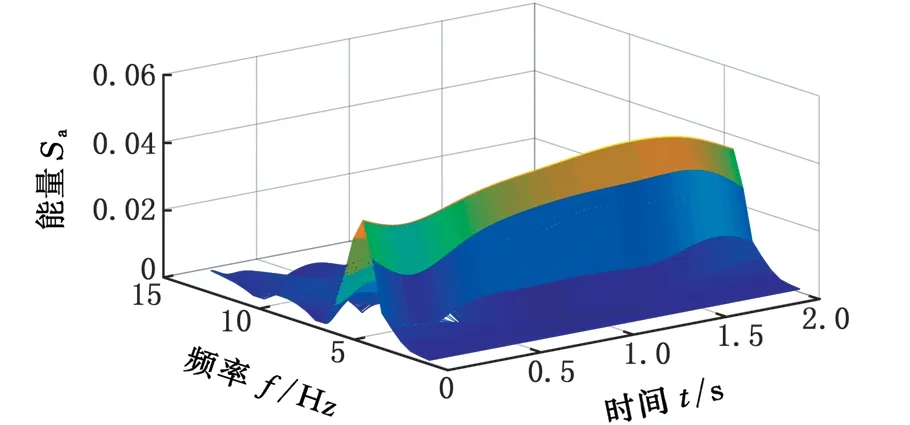
(c)蛇行异常图3 S变换后的模时频矩阵Fig.3 The module time-frequency matrix after S-transform
图3为高速列车分别在3 种状态(正常、小幅蛇行、蛇行异常)下的监测数据通过S变换后得到的一组模时频矩阵图。由图3a可以看出,当高速列车正常运行时,信号模时频矩阵的能量Sa在整个时频域范围内分布比较分散,且随着时间的推移,其频率成分的变化非常明显。但是总体来看,没有哪个频率成分是绝对的主导。由此也可从一个侧面说明列车在高速运行状态下,其振动信号是典型复杂的多分量、非平稳随机信号。鉴于以上分析,对高速列车的蛇行状态监测,必须考虑其振动信号的非平稳特性。由图3c可以看出,在蛇行异常状态下,信号模时频矩阵的频率成分随时间推移,其幅值变化不大,未见幅值明显发散的情况,监测信号总体上趋于平稳。这是由于当高速列车处于临界蛇行状态时,抗蛇行阻尼器阻碍了蛇行运动的进一步发散,避免了系统的进一步失稳,因此,在监测时间内,表现为系统极限环上的临界稳定的运动形式。此时,信号的频率特征较为明显,其主要能量集中在7 Hz左右,与蛇行运动的基本理论是相符的。图3b是高速列车处于正常和蛇行失稳之间即小幅蛇行状态时的信号模时频矩阵分布图。由图3b可以看出,此时的能量分布同样比较分散,但相对正常状态似乎在朝某个方向逐渐集中,峰值的频率成分明显右移,应该略大于蛇行异常时的主要频率。从系统角度分析,小幅蛇行是列车系统从一个稳定的平衡解状态(正常状态)转变为另一个稳定的周期解状态(临界失稳状态)过程中的一个系统转变过程。而图3b正是这种转变过程的具体表现,其模时频分布特征介于正常运行和蛇行异常振动信号的模时频分布特征之间,是一个逐渐从能量分散的非平稳信号到能量集中的基本平稳的信号转变过程。
3.3 最大时变特征函数的特征量提取
由图3分析可得,能量分布的不同是不同状态下模时频分布矩阵的最直观的区别,因此,选取该模时频分布矩阵中振动能量最为集中的频率点,对该模时频分布矩阵进行截取,即可快速构建一个简单的特征函数,从而将小幅蛇行运动识别出来。
定义能量最大处的时变特征函数为Vf(t),其表达式为
Vf=Sa(t,fb)
(14)
式中,t为采样时刻;fb为能量最高处的频率值。
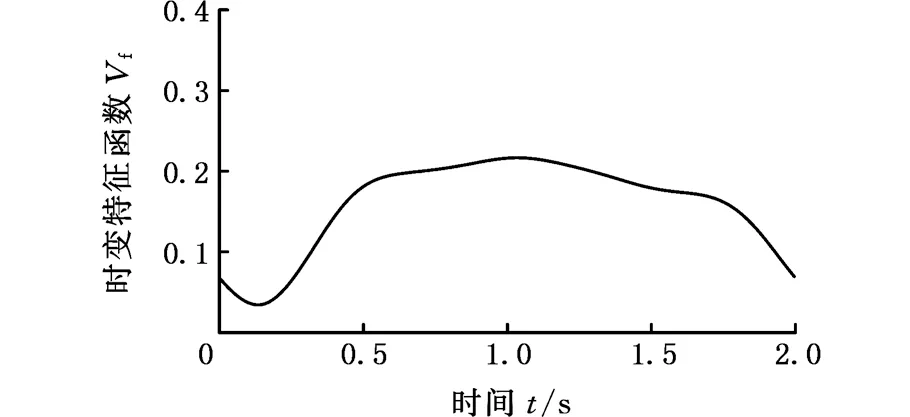
以图3所示的振动信号为例,求得相应的最大时变特征函数Vf(t)如图4所示。由图4可以看出,通过S变换后,3种状态的模时频矩阵能量分布差别很大。因此只需简单地提取模时频矩阵中的能量最大处的时变特征函数,并提取相关的统计特征指标,即可较好地实现状态分类。现对得到的模时频矩阵幅值时变特征函数在整个时间段上提取4个特征指标,分别为最大值(max)、最小值(min)、标准差(mean)、标准差值(std)。
根据对转向架横向振动信号最大能量对应的频率,确定模时频矩阵幅值时变特征函数Vf(t),对图4中的函数分别进行特征指标的提取,经归一化后,其特征指标如表1所示。
4 S变换方法结果对比分析
为验证S变换的有效性,本文采用小波变换方法进行对比研究。参照文献[15],小波基选为db2,小波分解设为四层,对小波分解最终的近似部分和四个细节部分的小波系数分别进行特征提取,提取的特征指标与Vf(t)提取的特征指标相同,分别为:小波系数的最大值、最小值、均值和标准差。表2所示为小波变换后对小波系数提取的一组特征指标。
为检验S变换特征提取方法对小幅蛇行的识别效果,将每种状态(正常、小幅蛇行、以及蛇行异常)的36组样本数据均分成两部分,18组作为训练样本,另外18组作为测试样本,采用LS-SVM来对高速列车的3种不同运行状态进行识别。LS-SVM分类过程中核函数为高斯核函数,设定惩罚因子c=2,核函数高度控制参数σ=0.2。在对支持向量机进行训练前,提取的三种状态的各类特征量指标需进行归一化处理,以保证所有的特征指标值都介于0~1之间。
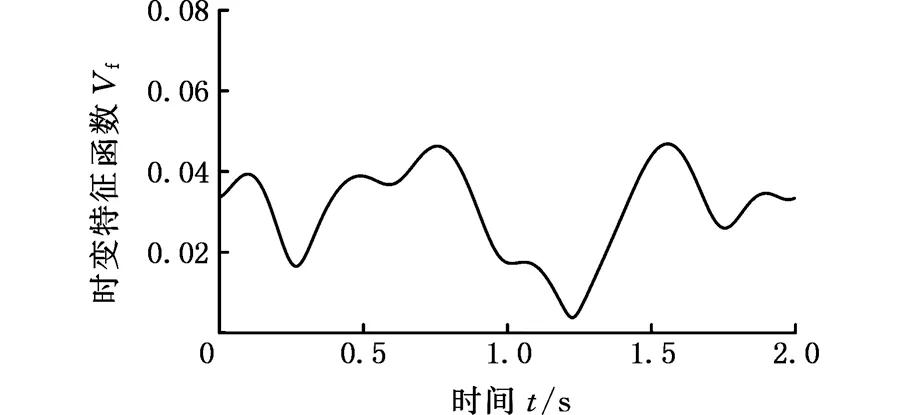
(a)正常
(b)小幅蛇行
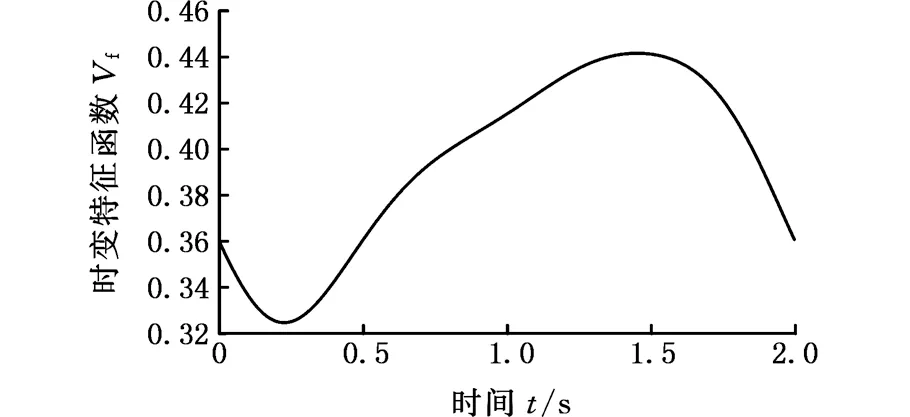
(c)蛇行异常图4 模时频矩阵中的能量最大处的时变特征函数Fig.4 The time-amplitude function at the maximum energy frequency point
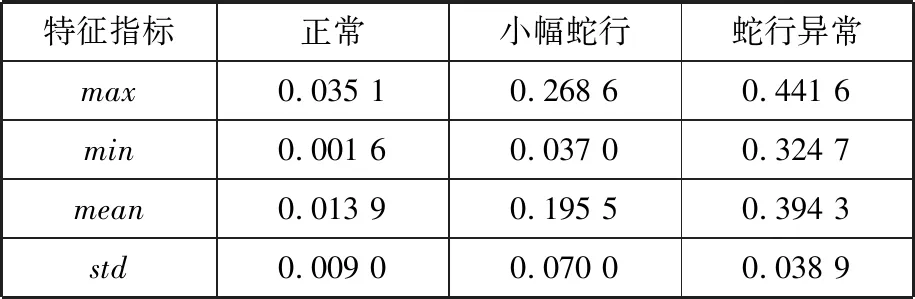
特征指标正常小幅蛇行蛇行异常max0.035 10.268 60.441 6min0.001 60.037 00.324 7mean0.013 90.195 50.394 3std0.009 00.070 00.038 9

表2 利用小波系数提取的特征指标
S变换特征指标和小波变换特征指标的分类识别结果如表3所示。由表3可以看出利用小波变换后的小波系数提取信号的时频特征,小波分解能把大部分状态区分开来,但是小波变换方法本身窗宽为固定值,且窗函数的选择对分析结果也有较大影响,导致其识别结果并不理想。采用S 变换后,由于S 变换采用高斯窗函数,并且设定窗宽与频率的倒数成正比,改善了小波变换窗宽固定的缺陷;同时,与小波变换相比,其时频分布中各频率分量的相位谱与原始信号保持直接的联系;此外, 经过S 变换提取的特征量对强噪声不敏感,从而使得同样的原始数据,基于S变换的时频特征提取以及识别结果明显优于小波变换识别结果。主要表现在两个方面:对于小幅蛇行的识别采用S变换特征指标的识别率要明显高于小波变换的特征指标的识别率;与此同时,对于每一组样本,S变换特征指标只有4个,小波变换的特征指标却有20个,S变换的特征指标个数要明显少于小波变换特征指标的个数。

表3 支持向量机识别结果对比
5 结语
小波变换是经典的非平稳信号的处理方法,其分辨率可调,广泛应用于非平稳信号特征提取当中,然而,小波变换窗宽为固定值,且窗函数的选择对分析结果也有较大影响,致使其对高速列车小幅蛇行识别效果并不理想。
高速列车转向架横向加速度信号具有非线性、非平稳的特点,传统的特征提取方法不能有效地提取信号特征。本文提出基于S变换的高速列车小幅蛇行特征提取方法,实现了对小幅蛇行的准确识别,并能对蛇行异常产生一定的预警作用。识别结果表明,基于S变换的时频特征提取方法优于基于小波变换的时频特征提取方法。
以上研究完全依据多次蛇行异常的在线实际监测数据,但是由于试验条件限制,现场采集的蛇行异常数据非常有限,目前分析的小幅蛇行信号仅仅来源于某次蛇行异常的在线测试数据,此次特征提取方法是否具有普遍意义,还需要进一步对小幅蛇行的演变机理进行研究。
