中红外光谱预测牛奶及奶产品成分含量的回归模型及其特点
2019-05-30阮健陈焱森万平民潘中保张震闫磊任小丽张淑君
阮健,陈焱森,万平民,潘中保,张震,闫磊,任小丽,张淑君
(1.华中农业大学,动物遗传育种与繁殖教育部实验室,武汉 430070;2.武汉金旭畜牧科技发展有限公司,武汉 430065;3.河南省奶牛生产性能测定中心,郑州 450046)
收稿日期:2018-08-20
基金项目:国家重点研发计划(2017YFD0501903);奶业技术体系岗位(CARS-36)资助。
通讯作者:张淑君,教授,博士生导师,主要研究方向为动物遗传育种与繁殖。
牛奶及其奶产品中物质含量丰富,中红外光谱(MIR)技术是一项能够快速、无损、定性、定量检测奶及奶产品中各种有机物与无机物的检测技术。其光谱条带密度与官能团的比例关系可用于定量分析[1]。为了建立准确度和精度高的预测模型,国内外研究人员对大量的建模方法进行了比较试验。使用正确的建模方法可以极大提高模型的健壮性,在进行外部验证时会得到较高的决定系数(R2)。回归建模方法主要分为线性和非线性两种,其中非线性方法的应用最广泛。除此之外,有些多用于分类分析的方法也可以用于回归建模。2006年,国外学者通过MIR成功建立了预测模型,可预测奶牛中大部分脂肪酸含量[2],并在后来的几年里,通过不断改进方法,提高了模型的预测准确性。2010年,科学家用MIR顺利预测了牛奶的蛋白质组成[3],2011年应用MIR预测了牛奶的真蛋白质含量[4]。在随后的几年中,建立了大量具有高精度的预测模型。在研究人员不断地尝试和选择中,根据均方根误差(RMSEP)和决定系数(R2)等参数大小,对模型进行了比较和评价。本文对这些常用于牛奶及奶产品中成分定量回归建模的方法及其特征给与介绍和总结,以期为我国以后相关研究及应用提供参考。
1 回归方法及其特征
1.1 偏最小二乘法(PLS)
牛奶及奶产品通过中红外光谱仪得到的MIR以及其转化的数据矩阵往往存在自变量之间的多重相关性,如果采用最小二乘法(LS),这种变量多重相关性会严重危害参数估计,扩大模型预测误差,影响模型稳定性。而偏最小二乘法(PLS)能规避这个问题。现行的校正方法即是偏最小二乘法(PLS)[5],偏最小二乘回归的基本作法是首先在自变量集中提出第一成分t1(t1是x1,x2,…,xm的线性组合,且尽可能多地提取原自变量集中的变异信息);同时在因变量集中也提取第一成分u1,并要求t1与u1相关程度达到最大。此方法运用了部分主成分分析法(PCA)的思想,PCA可以解决变量间共线性的问题。二者的不同在于PCA是从数据中抽提出的主成分进行回归,一般来说是选择自变量得分靠前的几个主成分,只考虑了自变量的主成分,所提取的主成分对自变量系统有很强的解释能力,它们是通过自变量之间的相关系数矩阵的特征值、特征向量得出的,包含了大部分自变量的变异信息,在提取主成分的过程中,与因变量是完全分开的,二者之间没有任何联系[6]。然后根据得分系数矩阵将原变量代回到所得的新模型中。而PLS不仅考虑了自变量的主成分得分,也考虑了自变量与因变量之间各自主成分的相关关系。因此,可以认为两种方法选择的主成分是不同的主成分,PCA筛选出的主成分t1是离差信息最大的方向,而PLS通常不是。因此,偏最小二乘回归是一种多因变量对多自变量的回归。通过PCA建立模型的时候,往往不能包括所有的样本信息,导致回归方程的拟合度较差。而使用PLS时,在最终模型中将包含原有的所有自变量。2009年,Mauer等[7]定量检测婴幼儿奶粉中的三聚氰胺,通过PLS建立奶粉中三聚氰胺浓度回归模型,其决定系数R2>0.99,交叉验证均方误RMSECV≤0.9,残差预测偏差RPD>12。光谱因子分析能够将未掺杂的婴儿配方奶粉与含有1ppm三聚氰胺的样品以99.99%的置信度分开,对样品区的分类准确无误。
1.2 最小二乘支持向量机(LS-SVM)
Lu等人基于最小二乘支持向量机(LS-SVM)建立了一种使用近红外光谱检测奶粉中纯三聚氰胺的新颖且快速的方法[8]。在应用红外光谱技术对奶粉中脂肪含量进行无损检测时,采用LS-SVM对光谱透射率和脂肪含量值进行建模时,模型对脂肪含量有较好的预测值,预测误差均方根(RMSEP)为0.8367[9]。支持向量机(SVM)是一种建立在结构风险最小化基础上的机器学习方法,具有小样本、非线性、高维度、预测精度高等特点。它在解决非线性问题上有很多特有的优势。SVM除了能处理分类问题和判别分析问题外,也能特别成功地处理回归问题。支持向量回归机的基本思想是寻求一个线性回归方程去拟合所有的样本点,它寻求的最优超平面不是将两类最大限度分开,而是使样本点离超平面总方差最小。分类问题中求得的超平面也可以用于解决回归问题。其算法是通过一个非线性映射φ,将数据x映射到高维特征空间F,并在这个空间进行线性回归。即

b为阈值。因此,它将实际问题通过非线性变换转换到高维的特征空间,在高维空间中构造线性决策函数来实现原空间中的非线性决策函数,回归建模将低维非线性的输入映射到高维线性的输出[10]。而LS-SVM是基于SVM算法的一种衍生算法。相对于SVM,LS-SVM把不等式的约束条件变成了等式约束,从而使拉格朗日乘子的求解方便许多,加快了求解速度[11]。但是LS-SVM的预测精度比SVM稍差一些。吴迪等[9,12]采用LS-SVM算法成功实现了奶粉中脂肪和蛋白质的无损检测,且预测结果要优于传统的PLS的预测结果。
1.3 人工神经网络(ANN)
在对汽油光谱数据进行处理时研究人员比较了包括ANN和PLS以及PCA等不同方法的准确性。结果表明,当数据是非线性时,ANN比PLS表现更好[13,14]。通过将一个隐层神经网络应用于平均中心吸收光谱,得到了实验数据的最佳结果[14]。Balabin等在用光谱法检测液态奶、婴儿配方奶粉和普通奶粉中的三聚氰胺时比较了多种回归方法。同样,对于非线性的数据,ANN比PLS有更好的表现[15]。ANN是受神经元的工作原理启发得来的,每一个神经元细胞通过树突接受从其他神经元细胞传来的电化学信号。当电化学信号的总强度达到一定阈值时,神经元便可以被激活,之后电化学信号通过突触被传送到与之相连的神经元。神经元之间的连接可以随着连通次数的增加而增强,对每个输入信号αi均要乘以连接系数wi来表示连接的强弱。所有信号乘以相应的连接系数并求和后需减去一定的阈值b。如果总和大于0,则神经元是激活的,若小于0,则神经元是抑制的。总信号∑ni=1Wiαi-b作为变量输入传递函数f(x),而传递函数的值是神经元后处理的信号,可以将其输出或者输入到下一个神经元[16]。神经网络的回归分析,是基于通过对样本的学习,来实现网络结构中自变量对应变量的映射的。也就是说神经网络不能得到简单的回归方程数学表达式,其结果是经过网络结构以及阈值等确定的。预测时,输入一个自变量,就会得到一个因变量作为结果输出[17]。ANN方法的主要缺点是其计算的复杂性和随机性。
1.4 贝叶斯回归(Bayes-R)
Ferragina等在对牛奶成分进行分析时比较了偏最小二乘法(PLS)、修改后-偏最小二乘法(MPLS)、贝叶斯岭回归(Bayes RR)、贝叶斯A(Bayes A)、贝叶斯B(Bayes B)共五个回归预测方法 。该实验从气相色谱分析的47个脂肪酸(FA)中选择了4个足以代表所有47个FA在饮食、生理、碳酸链长度(小、中、长)、FA结构中双键存在与否及比例等方面变化的FA作为参考物质,结果表明,与PLS和MPLS相比,剩下的三个方法表现出同样好的预测准确性[18]。贝叶斯模型的表现型是基于标准化光谱的线性回归模型:

其中β0是截距,{Xij}是标准化的波长数据,βj是每一个波长的效果,εi是假定为独立且相同分布的模型残差(iid),其中正态分布以零为中心,方差是σε2。鉴于上述假设,给定效果和方差参数的数据的条件分布是
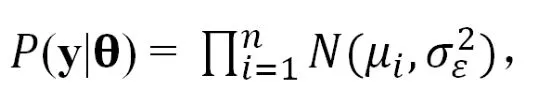
其中y= {yi},θ代表了收集到的模型参数,。先验密度是:
其中截距被指定为具有非常大方差的正态先验,这相当于把截距视为“固定”效应,残差方差被指定为自由度为dfε的倒数比例卡方(χ-2)比重和比例参数Sε,波长的影响被指定为由一组超参数Ω索引且随机独立同分布先验p(βj|Ω)。p(Ω)代表先验分布的超参数;p(βj|Ω)和p(βj|Ω)根据所述应用的模型而不同。贝叶斯岭回归(Bayes RR),贝叶斯A(Bayes A)和贝叶斯B(Bayes B)区别在于分配给效果的占优比重的形式不同。Bayes RR:在贝叶斯RR中,效果被赋予高斯先验。该规范将估计值缩小到零,贝叶斯A和贝叶斯B也发生了这种情况;收缩的程度在效果上是均匀的,并且该方法不执行变量选择[19,20]。Bayes A:在贝叶斯A中,(βj|Ω)iid~ t(βj|dfε,Sβ) 是一个t比例的密度,与高斯先验相比,其可引起效应估计的差异收缩,而与表型弱相关的预测因子的估计效应则向零强烈收缩,是具有强关联的预测因子的收缩,并随着反应缩小到较小程度[19,20]。Bayes B:p(βj|Ω)是零质量点和t比例密度的混合物,即:(βj|Ω)iid~ π×t(βj│dfε,Sβ)+(1-π)×1(βj=0) ,其中,π是先验概率,βj从t密度中得出。
2 小结
以上所列出来的是最常见的几种方法,在实际的科学研究和生产应用中更多使用的是以上方法的多种衍生算法。例如线性PLS(Linear-PLS)、多项式PLS(ploy-PLS)、样条函数拟合PLS(Spline-PLS)、神经元拟合PLS、非线性迭代PLS、BP人工神经网络(BP-ANN)等。通过中红外光谱对牛奶和奶产品中成分含量进行回归预测时,用于建模的方法多种多样,很难确定哪一种方法是最合适的,可使用多种方法进行分析,最后选择R2以及RPD最高以及RMSEP等误差参数最小的模型作为最终的预测模型。
