数形结合在初中数学教学中的运用分析

曾晓婵

（广州市增城区小楼中学，广东 广州 510000）

一、运用数形结合培养学生学习数学的兴趣

（一）抽象问题直观化

一些学生不喜欢数学的根本原因就是感觉数学太抽象，难以理解。初中阶段的学生主要以形象思维和主观思维为主，因此培养学生数学学习的兴趣，就需要把抽象的知识变的直观具体，让学生借助直观形象思维去理解抽象知识。而数形结合的教学思想可以把抽象的数与直观的形有效结合，加深学生对知识的理解，改变数学学习中单一枯燥的感觉，所以在数学教学中有效的运用数形教学思想，可以有效的激发学生学习数学的兴趣。

（二）理论联系实际

传统数学教育中教师侧重于学生基础知识的培养，忽略了数学来自生活应回归生活的重要作用，也导致了很多学生认为学习数学就是为了考试，在实际生活中没有什么作用的意识，逐渐失去学习数学的兴趣。因此初中数学教学应把握初中生的认知规律，将数学知识与学生实际生活联系起来，把现实中直观的问题加以抽象形成数学问题进行解决。这种思想方法可以把很多现实中的问题抽象成数学几何图形，利用代数知识解决问题。因此数形结合的运用可以更好的将理论与实际联系起来，从而提高学生学习兴趣。

（三）展现数学美

很多学生眼里的数学是枯燥无味的，但是数学世界里面的美感无处不在。学生对美的东西总会产生很大的兴趣，而兴趣是学生学习的动力，因此帮助学生发现数学里的美有利于提升学生学习的兴趣。比如黄金分割点是一个比值，但是利用它构成的图形都透漏出了美感等，利用数形结合的教学去展现数与形的统一美。

二、运用数形结合促进对数学概念的学习

初中数学概念是知识点的高度浓缩，是多次抽象的结果，这也是学生对概念难以理解的根本原因。但是初中数学的每一个概念都对应着直观的模型，教师要抓住这一特点，强化学生对概念的理，利用数形结合的教学思想，用概念对应的模型再现其形成过程，让学生从根本上去理解概念。

（一）加深对数学概念的理解记忆

每一个概念都能找到对应的模型，利用这个特点让学生明确概念形成的原因进而掌握概念。比如等式概念教学中，教师可以利用天平当做模型进行教学。学生对天平并不陌生，通过天平类比等式概念，学生很容易能抓住概念的中心含义。天平是两边对等，而等式也需要两边对等，学生能够从对天平认知的经验上实现对等式知识的构建。

（二）发现概念之间内在联系

数学具有系统性特征，当前具备的数学概念是后期学习概念的基础，有些学生在解题时找不到解题方式很大一部分原因就是没有把已有的数学知识结合。如何把单个的知识点有效结合，从不同的角度看待同一个知识问题，找到他们其中的内在联系是核心关键。利用数形结合理解知识时，就可以通过数和形两个方面去理解。例如学习解不等式组的解集时，拆开每个不等式的解法，学生就会，但一组合时，就无法找到不等式组的解集，所以这时最好就是结合数轴来解决问题。

三、数形结合与数学能力的培养

（一）发展学生直觉思维

直觉思维是指学生能够借助自己已具备的知识，对数学做出大胆合理的假设，直觉思维需要一定的数学知识做基础，也需要有一定的认知经验对数学进行推测。而数学知识中的几何图形是学生直觉思维发展的源泉，数形结合可以增加学生的图形储备，因此在数学教学中可以运用数形结合培养学生的直觉思维。

例如关于三角形的学习中，通过对三角形以及四边形的运动方向，从直观上去感觉图形的变化，从而得到三角形的稳定性特征。在数学解题时我们经常说的大胆猜测小心纠正，就是用直觉思维解题。

（二）培养学生形象思维能力

形象思维是通过头脑中的具体形象去解决问题的一项活动，在教学中运用数形结合教学思想，可以在增加学生图形储备的基础上发展学生的形象思维能力，数形结合能够把直观的图和抽象的数相结合强化学生的理解，也就是说学生在学习过程需要掌握和熟记代数的表示还需要记住代数表示对应的图形表示。比如在函数教学中，它的性质需要从图形上去感受，学生在对函数问题思考过程中就会想象函数图形，然后从图形中得出其性质，最后根据图形去解决问题，这样的过程就是形象思维。

（三）提高学生发散思维

发散思维是从不同的角度和层面上去分析同一个问题，通过正反面的比较开阔其视野活跃其思维，从而产生更多的独特的思想。因此培养学生的发散思维可以有效提升学生的创造思维，发展学生创新能力，进而提升学生数学素养。数形结合在培养学生的发散思维上，是通过数与形的不同角度和层面看待问题，这时学生对问题的思维程度不是固定的，而是一种活跃的状态，通过不同角度和层面的思考，形成独特的解题方式或者一体多解的方式。比如直线和圆的位置关系中，可以通过图形中两者相交点的个数去判断他们的位置关系；可以通过圆心与之间的距离进行判断，最后把圆形的判定与代数的判定相结合去思考问题。当学生在判定点数时，可以把两者的方程联系起来，通过求解个数判定位置关系。学生在这个过程中发散思维得到较好的提升。

（四）拓宽学生空间想象力

初中生空间想象力的培养不仅可以在几何教学中完成，在代数教学中也同样可以完成。几何具备直观形象的特点，代数具备规范、严谨的特点。数形结合的思想方法，就是要求要把表达形状大小的语言和具体的形状位置关系有效结合，建立一个对应的关系，而这种关系的建立体现了抽象思维活动，这就需要具备一定的空间想象能力才能完成。数形结合的思想需要学生注意数和形的联系，从数想到形从形在想到数。（例如在同一坐标系中标出 y1=x2，y2=x+3 的图像，x 取什么值时 y1〉y2；y1〈y2；y1=y2.（如图1所示）y1〉y2反映在图像中，两个函数之间的位置有什么关系。

图1

教师要引导写生进行思考和想象，当y1在y2的上面时得出y1〉y2.这样就能非常形象的得出结果。教师要引导学生运用数形结合的思想方式，让学生能够对利用‘形’把数量关系解释出来，发觉里面形的因素，提高解决问题的有效方式，进而发展学生的空间想象。

四、运用数形结合提高解题能力

通过解题可以帮助学生巩固所学知识，提高学生的解题能力。在初中数学教学中提高学生的解题能力是一项重点内容。数形结合的教学思想可以让学生把代数与图形有效结合，通过两者之间的交换，实现用代数解决几何问题，用几何法解决代数问题。初中数学中数轴的学习贯穿在整个有理数学习中，并且会直接影响到后期的坐标系学习，数轴是把数和点有效结合，利用数轴能够更加简洁的解答有理数问题。例如丨a-2丨+丨a-5丨+丨a-7丨求解最小值。在该题的求解中，绝对值在数轴上的几何意义表示距离。利用数形结合去解题，通过让学生利用数轴去解答，a到点2.5.7的距离和大于或等于点2到点7的距离，也就是说大于或等于5，因此该题能够直观的看到结果是5那么对应的点a=5.学生在利用数轴解答该题时能够更加快捷，并在这一过程中有重新复习了一遍绝对值的意义，加深了学生对知识的理解和记忆。

再例如在概率问题中数形结合思想方法是最常使用的方式，利用图形将机会均等的结果数和关注结果的发生数给列举出来，这样就形成一个较为直观的解决思路。如：班级组织班会，需要从两男两女中选取两位主持人，选出一男一女的概率。该题解答中，可以把男生假设为一号、二号，女生假设为一号、二号，然后做出所有机会均等发生的结果图。（见图2所示），从图中很直观的能看到，一男一女的结果数是8，所有机会均等的结果数为12。所以

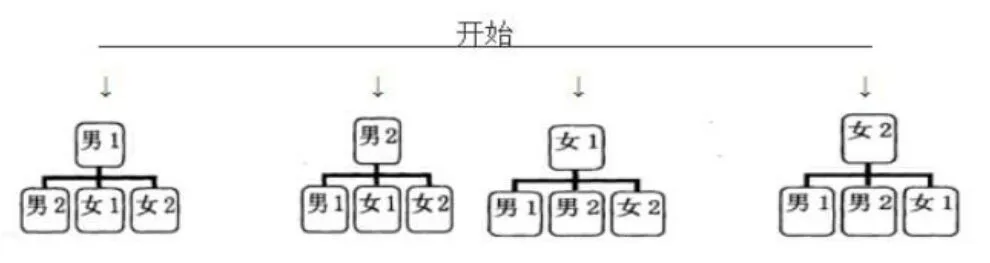
图2

教师在讲解数学习题时，要有意识的指导学生去挖掘习题中包含的知识，让学生通过教师指导形成正确的数形结合思维。无论是方程问题、函数问题、还是平面问题，都要探索其中隐藏的逻辑信息，合理利用图形背后的信息去解决实际问题。

五、结语

初中数学教学中数形结合是一种较为有效的思想方法，是通过数形之间的相互转化把抽象的问题变得更加具体，将复杂的问题变的更加加单的形式，加深学生对抽象知识的理解和内化，从而拓展学生的解题思路。作为一种重要的数学思想方法，学生对数形结合的掌握直接影响着他们后期数学的能力和发展。因此教师应注重这一教学思想的重要性把数形结合的思想方法逐步的渗透到日常教学当中。